In diesem Thema
- Verfügbare Analysen für nicht normalverteilte Daten
- Verwenden Sie diese Option Automatisierte Prozessfähigkeitsanalyse , um eine Methode auszuwählen
- Beispiel für die Verwendung Automatisierte Prozessfähigkeitsanalyse zum Auswählen einer Methode
- Bestimmen einer geeigneten Verteilung oder Transformation mit Identifikation der Verteilung.
- Beispiel für das Vergleichen der Anpassung von Verteilungen und Transformationen mit Identifikation der Verteilung
Verfügbare Analysen für nicht normalverteilte Daten
- Wählen Sie ein Verteilungsmodell mit Nicht-Normalverteilung aus, das an Ihre Daten angepasst ist, und analysieren Sie die Daten mit einer Prozessfähigkeitsanalyse für nicht normalverteilte Daten, z. B. mit Prozessfähigkeitsanalyse (nicht normal).
- Transformieren Sie die Daten, so dass die Normalverteilung ein geeignetes Modell darstellt, und verwenden Sie eine Prozessfähigkeitsanalyse für normalverteilte Daten, z. B. Prozessfähigkeitsanalyse für Normalverteilung.
- Wählen Sie eine verteilungsfreie Methode aus, die keine Annahmen über die Verteilung der Daten trifft, z. B Prozessfähigkeitsanalyse (nichtparametrisch). .
- Nutzen Sie technisches Fachwissen oder historische Daten des Prozesses.
- Meist empfiehlt es sich, auf technisches Fachwissen und historische Daten des Prozesses zurückzugreifen, um eine methode zu bestimmen, die an die Prozessdaten angepasst ist. Weisen die Daten z. B. eine symmetrische Verteilung auf? Welche Methode hat sich in der Vergangenheit für ähnliche Situationen bewährt?
- Verwenden Sie Bewertungen zur Güte der Anpassung.
- Der Anderson-Darling-Test bewertet, ob eine bestimmte Verteilung zu Daten aus einem Prozess passt. Wahrscheinlichkeitsnetze sind ein weiteres Werkzeug, mit dem bewertet werden kann, wie genau die Daten einer Verteilung folgen.
- Bewerten Sie, wie sich verschiedene Methoden auf Ihre Schlussfolgerungen auswirken.
- Wenn mehrere Methoden eine adäquate Anpassung an die Daten und ähnliche Schlussfolgerungen liefern, ist die Wahl weniger folgenreich. Umgekehrt, wenn Ihre Schlussfolgerungen von der Methode abhängen, möchten Sie möglicherweise die konservativste Schlussfolgerung melden oder weitere Informationen sammeln. Sie können z. B. die Verteilungsergebnisse von oder die Perzentile von verwenden, um zu sehen, wie Ihre Schlussfolgerungen von Automatisierte Prozessfähigkeitsanalyse Identifikation der Verteilung der Methode abhängen.
- Wenn Sie planen, im Laufe der Zeit wiederholte Prozessfähigkeitsanalysen für Ihren Prozess durchzuführen, versuchen Sie, eine Methode zu verwenden, die Ihren Prozess im Laufe der Zeit wahrscheinlich angemessen charakterisiert. Mit der gleichen Methode können Sie die Indizes aus den Wiederholungsanalysen einfach und direkt vergleichen.
- Nicht normalverteilungs- und verteilungsfreie Modelle verwenden die tatsächlichen Dateneinheiten. Das Normalenmodell aus einer Transformation verwendet transformierte Einheiten.
- Das normale Modell einer Transformation liefert Schätzungen sowohl der Gesamt- als auch der Prozessfähigkeit.
Verwenden Sie diese Option Automatisierte Prozessfähigkeitsanalyse , damit die Minitab Statistical Software dabei hilft, eine geeignete Methode zu ermitteln, die zu den Daten passt, und dabei die Nützlichkeit und Praktikabilität der Methode zu berücksichtigen. Bei der Analyse werden zuerst die Verteilungen und dann die Transformationen berücksichtigt. Wenn kein Modell zu den Daten passt, wird für die Analyse die verteilungsfreie Methode verwendet.
Um weitere Details zu den Daten anzuzeigen, verwenden Sie Identifikation der Verteilung. Die Analyse liefert Messungen für die Güte der Anpassung für verschiedene Methoden, um Ihre Entscheidung über die zu verwendende Methode zu unterstützen.
Verwenden Sie diese Option Automatisierte Prozessfähigkeitsanalyse , um eine Methode auszuwählen
Verwenden Sie diese Option Automatisierte Prozessfähigkeitsanalyse , um die Kompatibilität mehrerer Methoden mit den Daten zu bewerten und eine sinnvolle Auswahl zu treffen.
- Wählen
- Geben Sie an, ob Ihre Daten in einer einzelnen Spalte oder zeilenübergreifend angeordnet werden sollen.
- Geben Sie die Spezifikationsgrenzen für den Prozess ein.
Bei der Analyse werden Verteilungen und dann Transformationen berücksichtigt. Wenn keine parametrische Methode zu den Daten passt, wird für die Analyse die verteilungsfreie Methode verwendet. Die Ergebnisse enthalten einen Funktionsbericht für die erste Methode, der eine angemessene Anpassung bietet. Die Tabelle mit den Verteilungsergebnissen zeigt die Reihenfolge der Auswertung der Methoden, Informationen über die Anpassung der Methoden und Prozessfähigkeitsstatistiken. Sie können Ergebnisse für eine alternative Methode erzeugen, um die Methoden genauer zu untersuchen.
Beispiel für die Verwendung Automatisierte Prozessfähigkeitsanalyse zum Auswählen einer Methode
Ein Ingenieur sammelt Daten über das Ausmaß des Verzugs in keramischen Fliesen. Da die Datenverteilung unbekannt ist, führt sie anhand der Daten eine sinnvolle Methode für eine Identifikation der Verteilung Prozessfähigkeitsanalyse durch.
Die Tabelle der Verteilungsergebnisse zeigt die Reihenfolge der Auswertung der Methoden. In der ersten Zeile lautet die Schlussfolgerung für den Anderson-Darling-Test, dass die Daten keiner Normalverteilung auf dem Signifikanzniveau von 0,05 folgen, da der p-Wert kleiner als 0,05 ist. In der zweiten Zeile lautet die Schlussfolgerung für den Anderson-Darling-Test, dass die Weibull-Verteilung angemessen an die Daten angepasst ist, da der p-Wert größer als 0,05 ist. Die Prozessfähigkeitsergebnisse beziehen sich auf die Weibull-Verteilung, da die Weibull-Verteilung die erste Methode in der Liste ist, die eine vernünftige Anpassung bietet.
Anhand von Prozesskenntnissen prüfen die Ingenieure, ob die Weibull-Verteilung eine sinnvolle Methode ist. Beispielsweise hat die Weibull-Verteilung einen Rand bei 0. In den Daten ist 0 eine Grenze, die eine nicht verzerrte Kachel darstellt.
Die Analyse umfasst eine Prozessfähigkeitsanalyse, bei der die Weibull-Verteilung verwendet wird.
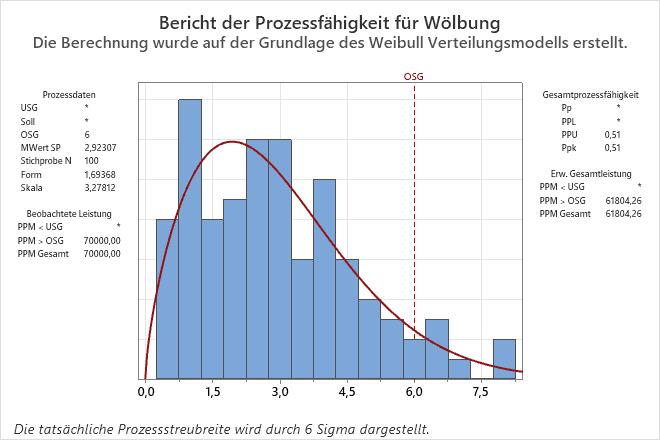
Ergebnisse der automatisierten Funktionsverteilung: Wölbung
| Verteilung | Lage | Skala | Schwellenwert | Form | P | Ppk |
|---|---|---|---|---|---|---|
| Normal | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | ||
| Lognormal | 0,8443 | 0,7444 | <0,005 | 0,4242 | ||
| Kleinster Extremwert | 3,8641 | 1,9924 | <0,01 | 0,5362 | ||
| Größter Extremwert | 2,0958 | 1,4196 | 0,212835 | 0,5130 | ||
| Gamma | 1,2477 | 2,3428 | 0,238337 | 0,4851 | ||
| Logistisch | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | ||
| Loglogistisch | 0,9097 | 0,4217 | <0,005 | 0,4090 | ||
| Exponential | 2,9231 | <0,0025 | 0,3780 | |||
| Weibull mit 3 Parametern | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | |
| Lognormal mit 3 Parametern | 1,3788 | 0,4184 | -1,4002 | 0,4961 | ||
| Gamma mit 3 Parametern | 1,2314 | -0,0197 | 2,3898 | 0,4864 | ||
| Loglogistisch mit 3 Parametern | 1,3043 | 0,2700 | -1,0940 | 0,4656 | ||
| Exponential mit 2 Parametern | 2,6679 | 0,2552 | <0,01 | 0,3982 | ||
| Box-Cox-Transformation | 1,6237 | 0,5380 | 0,574337 | 0,5116 | ||
| Johnson-Transformation | 0,0112 | 0,9949 | 0,798895 | 0,4959 | ||
| Nichtparametrisch | 0,6187 |
| Verteilung | Cpk |
|---|---|
| Normal | 0,5838 |
| Weibull* | |
| Lognormal | |
| Kleinster Extremwert | |
| Größter Extremwert | |
| Gamma | |
| Logistisch | |
| Loglogistisch | |
| Exponential | |
| Weibull mit 3 Parametern | |
| Lognormal mit 3 Parametern | |
| Gamma mit 3 Parametern | |
| Loglogistisch mit 3 Parametern | |
| Exponential mit 2 Parametern | |
| Box-Cox-Transformation | 0,5214 |
| Johnson-Transformation | |
| Nichtparametrisch |
Bestimmen einer geeigneten Verteilung oder Transformation mit Identifikation der Verteilung.
Verwenden Sie vor dem Durchführen einer Prozessfähigkeitsanalyse das Verfahren Identifikation der Verteilung, um zu bestimmen, welche Verteilung oder Transformation für die vorliegenden Daten am besten geeignet ist. Wenn keine Verteilung oder Transformation mit Ihren Daten kompatibel ist, sollten Sie Prozessfähigkeitsanalyse (nichtparametrisch).
- Wählen
- Wählen Sie aus, ob die Daten in einer einzelnen Spalte oder in Zeilen angeordnet sind.
- Wählen Sie oder Angeben und wählen Sie Alle Verteilungen und Transformationen verwenden bis zu 4 Verteilungen und Transformationen aus, die getestet werden sollen.
- Prozessfähigkeitsanalyse (nicht normal)
- Prozessfähigkeitsanalyse (nicht normal) für mehrere Variablen
- Capability Sixpack (nicht normal)
- Prozessfähigkeitsanalyse für Normalverteilung
- Capability Sixpack (Normalverteilung)
- Prozessfähigkeitsanalyse (Normalverteilung) für mehrere Variablen
- Prozessfähigkeitsanalyse (zwischen/innerhalb)
Beispiel für das Vergleichen der Anpassung von Verteilungen und Transformationen mit Identifikation der Verteilung
Ein Ingenieur sammelt Daten über das Ausmaß des Verzugs in keramischen Fliesen. Die Verteilung der Daten ist nicht bekannt, daher führt sie das Verfahren Identifikation der Verteilung für die Daten durch, um die Güte der Anpassung für die Exponentialverteilung und die Normalverteilung nach einer Johnson-Transformation zu vergleichen.
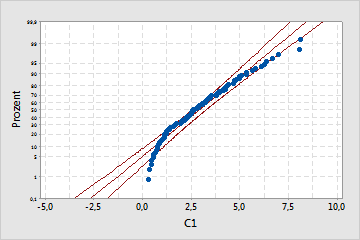
Exponentialverteilung
Dieses Wahrscheinlichkeitsnetz gibt an, dass die Exponentialverteilung keine gute Anpassung bietet; der p-Wert ist klein genug, um die Nullhypothese zurückzuweisen, dass die Daten einer Exponentialverteilung folgen.
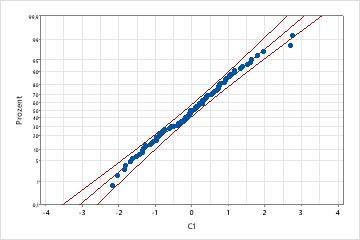
Normalverteilung mit Johnson-Transformation
Nach dem Anwenden einer Johnson-Transformation orientieren sich die Daten stärker an einer Normalverteilung, da der p-Wert groß ist und beinahe alle Datenpunkte innerhalb der Konfidenzgrenzen des Wahrscheinlichkeitsnetzes für Normalverteilung liegen.
