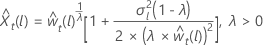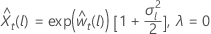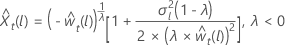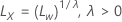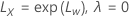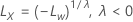使用最佳 ARIMA 模型进行预测 比较许多模型,并在分析规范中选择具有标准的最终模型。有关最终 ARIMA 模型的结果的信息,请转至 综合自回归移动平均 (ARIMA) 的方法和公式。以下各节包含 独有的 使用最佳 ARIMA 模型进行预测详细信息。
模型选择
模型选择使用以下步骤:
- 估计每个模型的模型参数。如果模型包含常量,并且参数的估计失败,请尝试在没有常量项的情况下估计参数。
- 计算每个模型的信息条件。默认条件是更正后的 Akaike 信息标准 (AICc)。
- 为具有最佳信息条件值的模型生成结果。
以下各节介绍了在选择非季节性和季节性型号时有所不同的详细信息。
非季节性型号
- 当您拟合具有常数项的模型时,候选模型的 p + q ≤ 9。
- 当拟合没有常数项的模型时,候选模型的 p + q ≤ 10。
- d = 2 的模型从不包含常量项。
- 该模型仅在 d = 1 时评估 ARIMA(0, d, 0)。
季节性模型
- 当您拟合具有常数项的模型时,候选模型具有 p + q + P + Q ≤ 9。
- 当拟合没有常数项的模型时,候选模型的 p + q + P + Q ≤ 10。
- d + D > 1 的模型从不包含常数项。
- 搜索季节性模型要求至少一个季节性参数的顺序能够大于 0。如果搜索的规范包括所有季节性参数的阶数均为 0 的模型,则搜索将包括非季节性模型。
- 在每个模型中,p、q、P 和 Q 中至少有 1 个不为零。
标准
- Akaike 信息准则 (AIC)
- 更正的 Akaike 信息标准 (AICc)
- 贝叶斯信息准则 (BIC)
模型的信息条件的计算使用模型的对数似然值。对数似然值的计算使用递归算法。欲了解更多信息,请参阅Brockwell & Davis (1991)1.
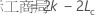
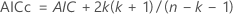

表示法
| 项 | 说明 |
|---|---|
| k | 模型中的参数数
|
| 断续器 | 当前模型的对数似然 |
| n | 时间序列的样本大小 |
Box-Cox 变换
该分析允许对数据进行 Box-Cox 变换。数据的转换发生在选择模型之前。有关时序数据的 Box-Cox 变换的信息,请转至 的方法和公式时间序列的 Box-Cox 变换。
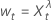 对于 λ > 0
对于 λ > 0 对于 λ = 0
对于 λ = 0 对于 λ < 0
对于 λ < 0
其中,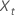 是原始时间序列的第 t 个 值, t = 1, ..., n。
是原始时间序列的第 t 个 值, t = 1, ..., n。
设 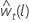 是从转换后的数据的原点 t开始的第 l个 预测值。设
是从转换后的数据的原点 t开始的第 l个 预测值。设  是转换后数据的 l步预测方差。然后,原始 序列的 t的第 l 个 预测值取决于 λ 的值:
是转换后数据的 l步预测方差。然后,原始 序列的 t的第 l 个 预测值取决于 λ 的值:
其中, 是原始刻度中的限制,并且
是原始刻度中的限制,并且  是转换后的刻度中的极限。
是转换后的刻度中的极限。
随机游走模型
ARIMA(0, 1, 0) 模型(带或不带常量项)是随机游走模型。在 Minitab 统计软件中, 使用最佳 ARIMA 模型进行预测 拟合随机游走模型。该命令 至少需要一个自回归或移动平均线参数。随机游走模型的估计和概率极限具有特定的形式。对数相似性、预测限和预测的概率限的计算取决于模型是否包含常量项。
定义:
| 项 | 说明 |
|---|---|
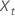 | t = 1, ..., n的时间序列的观测值 |
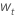 | 与原始时间序列的第一个差异数据,  |

或
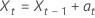
其中,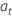 是独立且相同的分布,并遵循均值为 0 且方差 为 σ2, t = 2, ..., n的正态分布。
是独立且相同的分布,并遵循均值为 0 且方差 为 σ2, t = 2, ..., n的正态分布。
用常量表示模型的方程类似:

或
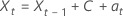

没有常量项的模型
日志相似性具有以下形式:
Loglikelihood
其中
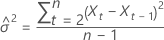

预测值的 100 × (1 – α) 概率限制 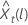 具有以下形式:
具有以下形式:
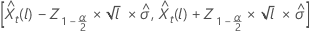
其中, 表示与标准正态分布相差的第 100 × (1 – α/2)个 百分位数。
表示与标准正态分布相差的第 100 × (1 – α/2)个 百分位数。
具有常量项的模型
对于具有常量的模型,对数相似性的计算需要估计常量 C。一、将数据与原始系列区分开来 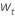 对于 t = 2, ..., n。常量是
对于 t = 2, ..., n。常量是 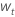 具有以下形式:
具有以下形式:
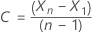
日志相似性具有以下形式:
Loglikelihood
其中
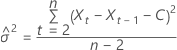
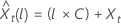
预测值的 100 × (1 – α) 概率限制 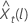 具有以下形式:
具有以下形式:
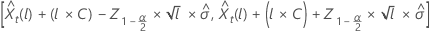
其中, 表示与标准正态分布相差的第 100 × (1 – α/2)个 百分位数。
表示与标准正态分布相差的第 100 × (1 – α/2)个 百分位数。