关于本主题
Box-Cox 变换
Box-Cox 变换的公式如下:
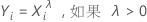


其中,Yi 是初始数据值,λ 是变换参数。当分析搜索 λ的最优值时,分析会将 λ 的最佳值舍入为 0.5 或最接近的整数以执行变换。
常见的 λ 值
下表显示一些常用的
λ 值及其变换。
| λ | 变换 |
|---|---|
| 2 | 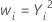 |
| 0.5 |  |
| 0 | 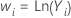 |
| -1 |  |
搜索最佳 λ
Minitab Statistical
Software使用1定义λ的最优值的标准和来自2 以搜索最佳值。该分析具有以下常规步骤:
- 将最佳值的标准定义为最小变异系数。
- 将系列划分为 H 子系列。
- 使用布伦特特的方法找到最小化变异系数的 λ 值。
以下各节定义了子系列和变异系数。
子系列
按季节时期将系列划分为子系列。如果季节周期未均匀划分为序列,请省略序列开头的其余观测值。如果分析的规范不包括季节性周期,则将季节性周期设置为 2。
例如,假设原始时间序列具有 10 个观测值,季节性周期为 4:{5, 6, 3, 2, 9, 8, 1, 7, 10, 4}.子级数为 10 模 4 = 2。由于 4 不能均匀地划分为 10,因此仅使用最后 8 个观测值来形成子系列。子系列是 {3, 2, 9, 8} 和 {1, 7, 10, 4}。
缺失值
如果子序列包含 1 个或更多缺失值,则在查找 λ 的最佳值时,从计算中省略子序列。搜索至少需要 2 个没有缺失值的子系列。
变异系数
使用以下定义计算变异系数:| 项 | 说明 |
|---|---|
| X1, X2, ... 断续器 | 原始时间序列中的观测值 |
| P | 原始时间序列的季节周期 |
| Xh, i | 子系列 h中的第 i个 观测值,其中 i=1, ..., P 和 h=1, ..., H |
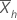 | hth 子系列的样本均值 |
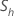 | hth 子系列的样本标准偏差 |
以下等式定义了每个子序列的统计数据:
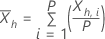
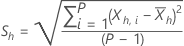
对于给定的 λ 和 h=1, ..., H 使用以下定义:
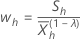
计算 W 统计量的样本平均值和样本标准差:
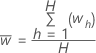

W 统计量的变异系数 (CV) 具有以下等式: 

使用 Brent 中的方法查找 λ 值,该值可使分析规范间隔内的 CV 最小化。分析将 λ 的最佳值舍入为 0.5 或最接近的整数以执行转换。
1 Guerrero,V.M.(1993)中的方法。功率变换支持的时间序列分析。Journal of
Forecasting 12(1), 37-48.
2 Brent,R.P.(1973)的方法,一种具有保证收敛性的算法,用于找到一个变量的最小函数。在
无导数的最小化算法 中(第 61-80 页)。普伦蒂斯大厅。
