请选择您所选的方法或公式。
系数
向后预测
向后预测值是使用指定的模型和当前迭代的参数估计值计算的。有关更多详细信息,请参阅 Cryer3。
SSE
公式

表示法
| 项 | 说明 |
|---|---|
| n | 观测值总数 |
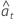 | 使用迭代参数估计值的残差,包括向后预测值 |
残差的 SS
公式
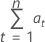
表示法
| 项 | 说明 |
|---|---|
| n | 观测值总数 |
| at | 使用最终参数估计值的残差,不包括向后预测值 |
残差的 DF
公式
对于包含常量项的模型:
(n – d) – p – q – 1
对于不包含常量项的模型:
(n – d) – p – q
表示法
| 项 | 说明 |
|---|---|
| n | 总观测值个数 |
| d | 差分个数 |
| p | 模型中包括的自回归参数的个数 |
| q | 模型中包括的移动平均参数的个数 |
残差的 MS
公式
SS/DF
卡方统计量
公式
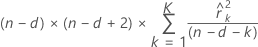
表示法
| 项 | 说明 |
|---|---|
| n | 观测值总数 |
| d | 差分个数 |
| K | 12、24、36、48 |
| k | 滞后 |
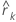 | 第 k个滞后的残差的自相关 |
卡方统计量的 DF
公式
对于包含常量项的模型:
K – p – q – 1
对于不包含常量项的模型:
K – p – q
表示法
| 项 | 说明 |
|---|---|
| K | 12, 24, 36, 48 |
| p | 模型中包括的自回归参数的个数 |
| q | 模型中包括的移动平均参数的个数 |
卡方统计量的 p 值
公式
P(X < χ2)
表示法
| 项 | 说明 |
|---|---|
| X | 以 χ2(DF) 形式分布 |
预测值
公式
预测是基于模型和参数估计值以递归方式计算的。例如,如果 ARIMA 模型与 1 个自递归项 (AR(1)) 和一个季节性周期为 12 的季节性差分项拟合,则说明此模型是拟合的:
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
要估计  (第一个预测值,其中 k 是原点),请查找:
(第一个预测值,其中 k 是原点),请查找:
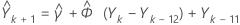
然后,按照同样的方式查找 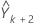 ,以此类推。
,以此类推。
要计算预测的 95% 预测间隔,首先必须计算权重。
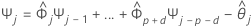
其中,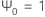 ,
, (对于 j < 0),并且
(对于 j < 0),并且  (对于 j > q)。
(对于 j > q)。
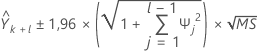
表示法
| 项 | 说明 |
|---|---|
| Yt | 时间 t 处的实际值 |
| Φ | 自回归项 |
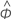 | 估计的自回归项 |
| γ | 常量项 |
| d | 差分个数 |
| p | 自回归参数个数 |
| q | 移动平均参数个数 |
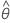 | 估计的移动平均项 |
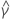 | 估计的常量项 |
| MS | 均方误 |
1 G.E.P. Box 和 G.M. Jenkins (1994)。Time Series Analysis: Forecasting and Control(时间序列分析:预测和控制),第 3 版。Prentice Hall.
2 W. Q. Meeker (1978)。“TSERIES-A User-Oriented Computer Program for Time Series Analysis”(TSERIES - 用于时间序列分析的面向用户的计算机程序),The American Statistician(美国统计学家),第 32 期,第 111-112 页。
3 J.D. Cryer (1986)。Time Series Analysis(时间序列分析)。Duxbury Press。
