ステップ1:標準偏差の比または分散の信頼区間を判断する
まず、サンプル分散またはサンプル標準偏差での比を考慮し、次に信頼区間を調べます。
サンプルデータの標準偏差および分散の推定比は、母集団標準偏差と母分散での比の推定値です。推定比は母集団全体ではなくサンプルデータに基づくため、サンプル比率が母比率に一致する可能性は低いと言えます。より良好に比を推定するためには、信頼区間を使用します。
信頼区間は、2つの母分散または標準偏差の間の比の値が含まれる可能性が高い範囲です。たとえば、95%の信頼水準は、母集団から100個のサンプルをランダムに採取した場合、そのうちおよそ95個からは母比率を含む区間が得られると期待することができます。信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広すぎて役に立たない場合、サンプルサイズを増加させることを検討します。 詳細は信頼区間の精度を高める方法を参照してください。
デフォルトで2サンプルの分散検定にはルヴィーンの方法とボネットの方法の結果が表示されます。ボネットの方法のほうが基本的にルヴィーンの方法よりも信頼度が高いです。しかし、極端に偏ったり裾の重い分布ではルヴィーンの方法のほうがボネットの方法よりも信頼度は高いです。F検定は、データが正規分布に従うことが確実な場合にのみ使用してください。正規性からのわずかな偏差があってもF検定の結果に大きく影響する可能性があるためです。詳細は、2サンプルの分散にBonettの方法またはLeveneの方法を使用する必要があるかを参照してください。
要約プロットには、比の信頼区間と、標準偏差または分散のどちらかの信頼区間が表示されます。
標準偏差の比
| 推定比 | Bonettを使用した比に対する 95%信頼区間 | Leveneを使用した比に対する 95%信頼区間 |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
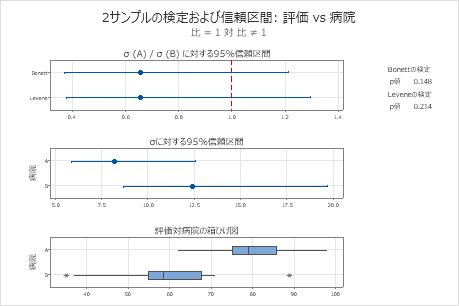
主要な結果:推定比、比の信頼区間、要約プロット
これらの結果では、2つの病院からの評価に対する標準偏差の推定母比率は0.658です。ボネットの方法によると、95%の信頼度で、病院の評価に対する標準偏差の母比率は0.372から1.215の間に含まれると考えることができます。
ステップ2:比が統計的に有意かどうかを判断する
- p値 ≤ α: 標準偏差または分散の比は統計的に有意です(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下します。母標準偏差または母分散の比は、仮説比と等しくならないと結論付けることができます。仮説比を指定しなかった場合、Minitabでは、標準偏差間または分散間に差がないかどうかを検定します(仮説率 = 1)。専門知識に基づいて、差が実際に有意かどうかを判断します。詳細は、統計的有意性と実質的有意性を参照してください。
- p値 > α: 標準偏または分散の比は統計的に有意ではありません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。母標準偏差または母分散の比は統計的に有意であると結論付けるだけの十分な証拠はありません。検定の検出力が、実質的に有意な差を検出するのに十分であることを確認してください。詳細は、2分散の検出力とサンプルサイズを参照してください。
- Bonettの検定では、すべての連続分布で正確な結果を出すことができ、データの正規性は要件ではありません。Bonettの検定は、通常、Leveneの検定より高い信頼性を示します。
- Leveneの検定も、すべての連続分布に関して正確です。歪みが極端で裾部が長い分布の場合は、Leveneの方法のほうがBonettの方法よりも信頼性が高くなります。
- F検定は、正規分布に従うデータの場合にのみ正確です。正規性からの偏差があると、サンプルサイズが大きい場合でも、F検定の結果が不正確になる可能性があります。ただしデータが正規分布によく適合する場合は、通常、F検定のほうがBonettの検定やLeveneの検定よりも強力になります。
詳細は、2サンプルの分散にBonettの方法またはLeveneの方法を使用する必要があるかを参照してください。
検定
| 帰無仮説 | H₀: σ₁ / σ₂ = 1 |
|---|---|
| 対立仮説 | H₁: σ₁ / σ₂ ≠ 1 |
| 有意水準 | α = 0.05 |
| 方法 | 検定統計量 | DF1 | DF2 | p値 |
|---|---|---|---|---|
| Bonett | 2.09 | 1 | 0.148 | |
| Levene | 1.60 | 1 | 38 | 0.214 |
主要な結果:p値
この結果で、帰無仮説では、2つの病院の評価の標準偏差の比が1であると仮定します。両方のp値が有意水準の0.05より大きいため、帰無仮説を棄却できず、病院の評価の標準偏差が異なると結論付けることはできません。
ステップ3:データに問題があるか確認する
歪みや外れ値などのデータの問題は、結果に悪影響を及ぼす可能性があります。グラフを使用して歪みを探し(各サンプルの広がりを調べて)、潜在的な外れ値を識別します。
データの広がりを調べ、データが歪んでいるかどうかを判断します。
データが歪んでいる場合、ほとんどのデータがグラフの上下に位置していることになります。ヒストグラムや箱ひげ図では歪みを検出するのが最も簡単であるケースが多いです。
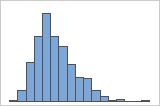
右方向の歪み
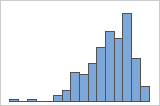
左方向の歪み
右に歪んだデータによるヒストグラムには、待ち時間が表示されます。待ち時間のほとんどは比較的短く、ごく少数の待ち時間だけが長くなります。左に歪んだデータによるヒストグラムには、故障時間データが表示されます。少数の項目が直ちに故障し、より多くの項目が後で故障します。
データが大きく歪んでいると、サンプルサイズが小さい場合(どちらかのサンプルが15未満)にp値の妥当性が影響を受けます。データが大きく歪んでいて、サンプルサイズが小さい場合はサンプルサイズを増やすことを検討します。
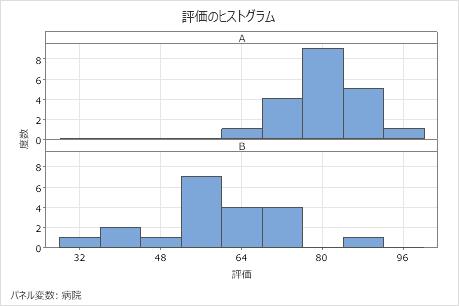
このヒストグラムでは、データは大きく歪んでいるようには見えません。
外れ値を特定
外れ値は、他の大部分のデータから遠くに離れているデータ値のことで、分析の結果に大きな影響を及ぼします。多くの場合、外れ値は、箱ひげ図で容易に識別できます。
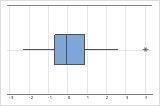
箱ひげ図では、アスタリスク(*)が外れ値を意味します。
外れ値がある場合は、その原因を特定してください。データ入力誤差や測定誤差はすべて修正します。異常な1回だけの事象(特殊原因とも呼ばれます)を示すデータ値を除外することを検討してください。それから、分析を繰り返します。詳細は、外れ値の識別を参照してください。

要約プロットにあるこの箱ひげ図では、病院Bのデータに2つの外れ値があります。
