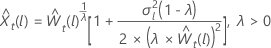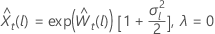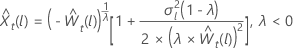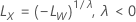ベスト ARIMA モデルによる予測 多くのモデルを比較し、解析の仕様の基準を持つ最終モデルを選択します。最終的な ARIMA モデルの結果については、「」 ARIMA (自己回帰和分移動平均)の方法と計算式を参照してください。以下のセクションでは、 に固有の詳細について説明します ベスト ARIMA モデルによる予測。
モデル選択
モデルの選択では、次の手順を使用します。
- すべてのモデルのモデルパラメータを推定します。モデルに定数が含まれていて、パラメータの推定が失敗した場合は、定数項なしでパラメータを推定してみてください。
- 各モデルの情報量基準を計算します。デフォルトの基準は、修正された赤池情報量基準 (AICc) です。
- 情報量基準の最適な値を持つモデルの結果を生成します。
以下のセクションでは、非季節モデルと季節モデルの選択が異なる詳細について説明します。
非季節モデル
- 定数項を持つモデルを適合する場合、候補モデルはp + q ≤ 9になります。
- 定数項のないモデルを適合する場合、候補モデルはp + q ≤ 10になります。
- d = 2 のモデルには定数項が含まれません。
- このモデルでは、d = 1 の場合にのみ ARIMA(0, d, 0) が評価されます。
季節モデル
- 定数項を持つモデルを適合する場合、候補モデルはp + q + P + Q ≤9になります。
- 定数項のないモデルを適合する場合、候補モデルはp + q + P + Q ≤10になります。
- d + D が 1 のモデル>定数項は含まれません。
- 季節モデルを検索するには、季節パラメータの少なくとも 1 つの順序を 0 より大きくする必要があります。検索の仕様に、すべての季節パラメータの次数が 0 のモデルが含まれている場合、検索には非季節モデルが含まれます。
- p、q、P、および Q のうち少なくとも 1 つは、すべてのモデルでゼロ以外です。
条件
- 補正赤池情報量基準(AICc)
- 赤池情報量基準(AICc)の修正
- ベイズ情報量基準 (BIC)
モデルの情報基準の計算では、モデルの対数尤度値が使用されます。対数尤度値の計算には、再帰アルゴリズムが使用されます。詳細については、Brockwell & Davis (1991)1。

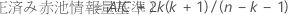
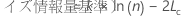
表記
| 用語 | 説明 |
|---|---|
| k | モデル内のパラメータの数
|
| ティッカー | 現在のモデルの対数尤度 |
| n | 時系列のサンプルサイズ |
ボックス-コックス変換
この分析により、データのボックスーコックス変換が可能になります。データの変換は、モデル選択の前に行われます。時系列データのボックスーコックス変換の詳細については、を参照してください の方法と計算式時系列のBox-Cox変換。
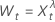 λ > 0
λ > 0 λ = 0 の場合
λ = 0 の場合 λ に対して < 0
λ に対して < 0
ここで、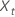 は元の時系列のtth 値であり、 t = 1, ..., n です。
は元の時系列のtth 値であり、 t = 1, ..., n です。
次のように定義します。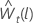 は、変換されたデータの原点 tから始まる l番目の 予測値です。次のように定義します。
は、変換されたデータの原点 tから始まる l番目の 予測値です。次のように定義します。 は、変換されたデータからの Lステップ予測差異です。次に、元の系列の t からの l番目の 予測値は、 λの値に依存します。
は、変換されたデータからの Lステップ予測差異です。次に、元の系列の t からの l番目の 予測値は、 λの値に依存します。
ここで、 は元のスケールの限界であり、
は元のスケールの限界であり、 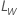 は、変換されたスケールの限界です。
は、変換されたスケールの限界です。
ランダムウォークモデル
ARIMA(0, 1, 0) モデルは、定数項の有無にかかわらず、ランダムウォークモデルです。Minitab統計ソフトウェアで、 ベスト ARIMA モデルによる予測 ランダムウォークモデルに適合します。このコマンド には、少なくとも 1 つの自己回帰パラメーターまたは移動平均パラメーターが必要です。ランダムウォークモデルの推定限界と確率限界には、特定の形式があります。対数尤度、予測限界、および予測の確率限界の計算は、モデルに定数項が含まれているかどうかによって異なります。
定義:
| 用語 | 説明 |
|---|---|
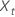 | t = 1, ..., nの時系列の観測値 |
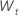 | 元の時系列からの最初の差分データ、  |
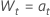
または
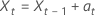
ここで、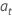 は独立かつ同一に分布しており、平均 0 と分散 σ2, t = 2, ..., nの正規分布に従います。
は独立かつ同一に分布しており、平均 0 と分散 σ2, t = 2, ..., nの正規分布に従います。
モデルを定数で表す方程式は似ています。

または
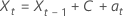

定数項のないモデル
対数尤度には、次の形式があります。
対数尤度
ここで、
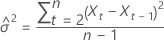

予測値の 100 × (1 ~ α) の確率制限 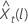 次の形式があります。
次の形式があります。
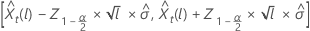
ここで、 は、標準正規分布から 100 × (1 – α/2)番目の 百分位数を表します。
は、標準正規分布から 100 × (1 – α/2)番目の 百分位数を表します。
定数項を持つモデル
定数を持つモデルの場合、対数尤度の計算には定数 C の推定 が必要です。まず、データを元の系列と区別します。 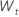 t = 2, ..., n の場合。定数は、
t = 2, ..., n の場合。定数は、 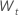 次の形式になります。
次の形式になります。
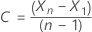
対数尤度には、次の形式があります。
対数尤度
ここで、
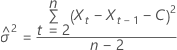
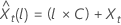
予測値の 100 × (1 ~ α) の確率制限 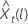 次の形式があります。
次の形式があります。
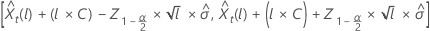
ここで、 は、標準正規分布から 100 × (1 – α/2)番目の 百分位数を表します。
は、標準正規分布から 100 × (1 – α/2)番目の 百分位数を表します。