このトピックの内容
ボックス-コックス変換
ボックスーコックス変換は、次の式で与えられます。

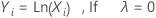

ここで、Yiは元のデータ値、λは変換のパラメータです。解析で λ の最適値を検索すると、 λの最適値が 0.5 または最も近い整数に丸められて変換が実行されます。
共通のλ値
次の表は、一般的に使用されるλ値の一部とその変換を示しています。
| λ | 変換 |
|---|---|
| 2 | 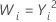 |
| 0.5 |  |
| 0 |  |
| -1 |  |
最適なλを探す
Minitab統計ソフトウェアは、1λの最適値の基準と2 をクリックして最適な値を検索します。分析には、次の一般的な手順があります。
- 最適値の基準を最小変動係数として定義します。
- 系列を H サブ系列に分割します。
- ブレントの方法を使用して、変動係数を最小化するλの値を求めます。
以下のセクションでは、サブ系列と変動係数を定義します。
サブシリーズ
系列を季節期間別にサブ系列に分割します。季節期間が系列に均等に分割されない場合は、系列の先頭からの残りの観測値を省略します。分析の仕様に季節期間が含まれていない場合は、季節期間 = 2 を設定します。
たとえば、10個の観測値と4の季節期間を持つ元の時系列とします。{5, 6, 3, 2, 9, 8, 1, 7, 10, 4}.サブ系列の数は 10 モジュロ 4 = 2 です。4は10に均等に分割されないため、最後の8つの観測値のみを使用してサブ系列を形成します。サブ系列は {3, 2, 9, 8} と {1, 7, 10, 4} です。
欠損値
サブ系列に 1 つ以上の欠損値が含まれている場合は、λ の最適値の検索でそのサブ系列を計算から除外します。検索には、欠損値のない少なくとも 2 つのサブ系列が必要です。
変動係数
変動係数を計算するには、次の定義を使用します。| 用語 | 説明 |
|---|---|
| X1、 X2、...ティッカー | 元の時系列の観測値 |
| P | 元の時系列の季節期間 |
| Xh、 i | サブ系列 hにおける i番目の 観測値 ( ここで、i=1, ..., P および h=1, ..., H) |
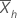 | h番目の 部分系列のサンプル平均 |
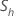 | h番目の 部分系列のサンプル標準偏差 |
次の式は、各サブ系列の統計量を定義します。
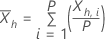
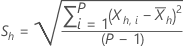
与えられた λ と h=1 の ... 、H は次の定義を使用します。
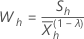
W 統計量のサンプル平均とサンプル標準偏差を計算します。

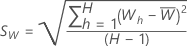
W 統計量の変動係数 (CV) の式は次のとおりです。


ブレントの方法を使用して、分析の仕様から区間内のCVを最小化するλの値を求めます。この解析では、λ の最適値を 0.5 または最も近い整数に丸めて変換を実行します。
1 GuerreroGuerrero, V.M. (1993)の方法を使用しています。検出力変換によってサポートされる時系列分析。Journal of Forecasting 12(1), 37-48.
2 BrentBrent、R. P. (1973)1つの変数の関数の最小値を見つけるための収束が保証されたアルゴリズムからの方法を定義する。 デリバティブなしの最小化のためのアルゴリズム (pp. 61-80)で。プレンティスホール。
