目的の方法または計算式を選択します。
係数
後方予測値
後方予測値は、指定したモデルと現在の反復のパラメータ推定値を使用して計算されます。詳細は、Cryer3を参照してください。
残差平方和(SSE)
計算式

表記
| 用語 | 説明 |
|---|---|
| n | 合計観測数 |
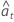 | 後方予測を含む、反復のパラメータ推定値を使用する残差 |
残差のSS
計算式
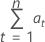
表記
| 用語 | 説明 |
|---|---|
| n | 合計観測数 |
| at | 後方予測を除外し、最終パラメータ推定値を使用する残差 |
残差のDF
計算式
定数項を含むモデルの場合:
(n – d) – p – q – 1
定数項を含まないモデルの場合:
(n – d) – p – q
表記
| 用語 | 説明 |
|---|---|
| n | 合計観測数 |
| d | 差の数 |
| p | モデルに含まれる自己回帰パラメータの数 |
| q | モデルに含まれる移動平均パラメータの数 |
残差のMS
計算式
平方和(SS)自由度(DF)
カイ二乗統計量
計算式
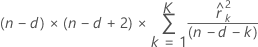
表記
| 用語 | 説明 |
|---|---|
| n | 合計観測数 |
| d | 差の数 |
| K | 12, 24, 36, 48 |
| k | 遅れ |
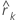 | k番目の遅れでの残差の自己層化 |
カイ二乗統計量のDF
計算式
定数項を含むモデルの場合:
K – p – q – 1
定数項を含まないモデルの場合:
K – p – q
表記
| 用語 | 説明 |
|---|---|
| K | 12, 24, 36, 48 |
| p | モデルに含まれる自己回帰パラメータの数 |
| q | モデルに含まれる移動平均パラメータの数 |
カイ二乗統計量のp値
計算式
P(X < χ2)
表記
| 用語 | 説明 |
|---|---|
| X | χ2(DF)として分布 |
予測
計算式
予測値は、モデルとパラメータの推定値に基づいて再帰的に計算されます。たとえば、ARIMAモデルが、自己回帰項(AR(1))1つと、季節期間が12の季節階差項1つを含む適合である場合、このモデルは適合です。
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
最初の予測 (kは原点)を推定するには、次を求めます。
(kは原点)を推定するには、次を求めます。
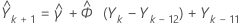
次に、同じ方法で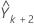 を求め、以下同様に計算します。
を求め、以下同様に計算します。
予測の95%予測区間を計算するには、まず重みを計算する必要があります。
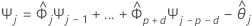
ここで、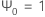 ,
,  j< 0およびの場合の
j< 0およびの場合の j>q.の場合。
j>q.の場合。
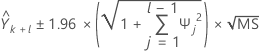
表記
| 用語 | 説明 |
|---|---|
| Yt | 時間tでの実際の値 |
| Φ | 自己回帰項 |
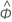 | 推定自己回帰項 |
| γ | 定数項 |
| d | 差の数 |
| p | 自己回帰パラメータ数 |
| q | 移動平均パラメータの数 |
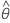 | 推定移動平均項 |
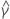 | 推定定数項 |
| MS | 誤差の平均平方 |
1 G.E.P. Box and G.M. Jenkins (1994). Time Series Analysis: Forecasting and Control, 3rd Edition. Prentice Hall
2 W. Q. Meeker (1978). "TSERIES-A User-Oriented Computer Program for Time Series Analysis", The American Statistician, 32, 111-112
3 J.D. Cryer (1986). Time Series Analysis. Duxbury Press.
