Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
- Formules générales - Effectif d'échantillon pour les intervalles de tolérance
- Calcul de l'effectif de l’échantillon pour les intervalles de tolérance normaux
- Calcul du pourcentage maximal de la population dans l'intervalle pour les intervalles de tolérance normaux
- Calcul de l'effectif d'échantillon et des pourcentages maximaux acceptables de la population de l'intervalle pour les intervalles de tolérance non paramétriques
Formules générales - Effectif d'échantillon pour les intervalles de tolérance
Définition d'un intervalle de tolérance (bilatéral)
Soit X1, X2, ..., Xn les valeurs ordonnées d'un effectif d'échantillon aléatoire n d'une loi de distribution continue.Soit la fonction de répartition F(χ,θ) pour Ω dans un espace de paramètre avec une dimension supérieure ou égale à 1.
Soit L < U deux statistiques basées sur l'échantillon de sorte que pour toutes les valeurs données α et P, avec 0 < α < 1 et 0 < P < 1, la formule suivante est valide pour tous les θ dans Ω :
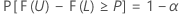
Enfin, l'intervalle [L, U] est un intervalle de tolérance bilatéral avec un contenu égal à P x 100 % et un niveau de confiance égal à 100(1 - α) %. Cet intervalle peut être appelé intervalle de tolérance bilatéral (1 - α, P). Par exemple, si α = 0,10 et que P = 0,85, l'intervalle obtenu est appelé intervalle de tolérance bilatéral (90 %, 0,85).
Effectif de l'échantillon et marge d'erreur
Soit C = F(U) – F(L). Un intervalle de tolérance bilatéral (1 –α, P) est exprimé comme suit :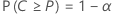
- La probabilité que l'intervalle couvrira au moins 100P % de la population est 1 – α.
- La probabilité, α*, est si faible que l'intervalle couvrira plus de 100P* % de la population, où P* = P + ε et ε > 0.
En d'autres termes, pour les valeurs données de P, α, ε et α*, l'effectif de l'échantillon est déterminé de sorte que
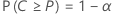
et

Cette approche repose sur le fait que, pour tout élément P* > P, P(C > P*), il existe une fonction décroissante de l'effectif de l'échantillon et il peut donc être utilisé pour déterminer la précision.
Choisir une petite valeur de ε et de α* réduit l'intervalle de tolérance, raison pour laquelle un effectif d'échantillon plus important est nécessaire. Les valeurs typiques de ε et de α* sont 0,10, 0,05 ou 0,01.
Remarque
Les définitions et concepts ci-dessus sont également applicables aux intervalles de tolérance unilatéraux.
- Faulkenberry, G.D. and Weeks, D.L. (1968). Sample size determination for tolerance limits. Technometrics, 10, 343-8.
Calcul de l'effectif de l’échantillon pour les intervalles de tolérance normaux
Intervalle unilatéral
Les auteurs Faulkenberry et Daly1 montrent que pour des valeurs données de α, P, ε et α*, l'effectif d'échantillon requis pour un intervalle unilatéral est obtenu par la recherche de la valeur minimale de n qui satisfait l'équation suivante :

où la notation tx,y(d) représente le ye percentile d'une loi t non centrale avec x degrés de liberté et le paramètre de non-centralité d. Les paramètres de non-centralité δ et δ* sont calculés comme suit :

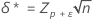
où zp correspond au Pe percentile de la loi normale standard.
Minitab utilise un algorithme itératif pour obtenir la valeur minimale requise pour n.
Intervalle bilatéral
Pour connaître les calculs de l'effectif d'échantillon d'un intervalle bilatéral reposant sur la fonction I( k, n, P), reportez-vous à la rubrique Méthodes et formules pour les intervalles de tolérance (loi normale) et cliquez sur "Intervalles de tolérance exacts pour les lois normales".
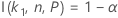
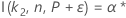
Minitab utilise un algorithme itératif pour obtenir la valeur minimale requise pour n. Pour plus d'informations, reportez-vous à la publication d'Odeh, Chou et Owen2.
Notation
| Terme | Description |
|---|---|
| 1 – α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| ε | marge d'erreur de l'intervalle de tolérance |
| α* | probabilité de la marge d'erreur de l'intervalle de tolérance |
| n | nombre d'observations dans l'échantillon |
- Faulkenberry, G.D. and Daly, J.C. (1970). Sample size for tolerance limits on a normal distribution. Technometrics, 12, 813–21.
- Odeh, R. E., Chou, Y.-M. et Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Calcul du pourcentage maximal de la population dans l'intervalle pour les intervalles de tolérance normaux
P* = P + ε
Les calculs de la marge d'erreur sont semblables à ceux de l'effectif d'échantillon décrits dans la rubrique Formules générales - Effectif d'échantillon pour les intervalles de tolérance.
Intervalles unilatéraux
Pour les valeurs données de n, α, P et α *, la marge d'erreur ε d'un intervalle unilatéral est obtenue par la résolution de δ* dans l'équation suivante :
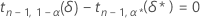
où la notation tx,y(d) représente le ye percentile d'une loi t non centrale avec x degrés de liberté et le paramètre de non-centralité d. Minitab utilise un programme de détection de racine numérique pour calculer δ*. Une fois la valeur de δ* déterminée, la valeur de ε peut être obtenue à partir de la formule suivante :

Intervalles bilatéraux
Les calculs de la marge d'erreur d'un intervalle bilatéral reposent sur la fonction I (k, n, P), qui est décrite dans la rubrique Intervalles de tolérance exacts pour les lois normales.
Pour les valeurs données de n, α, P et α*, la marge d'erreur ε d'un intervalle bilatéral est obtenue à l'aide de l'algorithme décrit par les auteurs Odeh, Chou et Owen1. Commencez par résoudre l'équation suivante pour k :


Notation
| Terme | Description |
|---|---|
| 1 – α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| P* | pourcentage maximal de la population dans l'intervalle |
| ε | marge d'erreur de l'intervalle de tolérance |
| α* | probabilité de la marge d'erreur de l'intervalle de tolérance |
| n | nombre d'observations dans l'échantillon |
- Odeh, R. E., Chou, Y.-M. et Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Calcul de l'effectif d'échantillon et des pourcentages maximaux acceptables de la population de l'intervalle pour les intervalles de tolérance non paramétriques
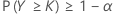
C'est-à-dire n – k = FW–1 (1 – α), où FW–1(.) représente la fonction de répartition inverse de W = n – Y.
De même, une limite supérieure de tolérance unilatérale (1 – α, P) est exprimée par X(n – k + 1), où k satisfait les conditions ci-dessus pour la limite inférieure.
Dans les deux cas, la couverture réelle ou effective est exprimée par P(Y > k).
En outre, un intervalle de tolérance bilatéral (1 – α, P) peut être exprimé par (Xr, Xs), où k = s – r est le plus petit entier satisfaisant la condition suivante :
Prendre s = n – r + 1 de sorte que r = (n – k + 1) / 2 est devenu une pratique courante. r et s sont arrondis à l'entier inférieur. La couverture réelle ou effective est exprimée par P(V ≤ k – 1).
Critère
Le critère des calculs d'effectif d'échantillon pour les intervalles de tolérance non paramétriques (unilatéraux ou bilatéraux) est semblable à celui décrit pour les données normales. Plus particulièrement, pour une limite inférieure de tolérance unilatérale (1 – α, P), le critère consiste à déterminer l'effectif de l'échantillon, n, et le plus grand entier k satisfaisant les conditions suivantes :
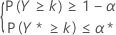
Cette condition équivaut à déterminer n et le plus grand entier k satisfaisant les conditions suivantes :
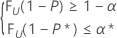
où FU(.) représente la fonction de répartition d'une variable aléatoire U qui est distribuée comme une loi bêta avec les paramètres α = k et b = n – k + 1.
Comme souligné dans l'ouvrage de Hahn et Meeker1, le critère génère des exigences d'effectif d'échantillon identiques pour les intervalles de tolérance unilatéraux et bilatéraux. Par conséquent, nous utilisons le critère ci-dessus pour les intervalles de tolérance unilatéraux et bilatéraux.
Pour des valeurs données de ε, P et α*, Minitab utilise un algorithme itératif pour trouver l'effectif d'échantillon minimal satisfaisant les deux conditions ci-dessus. Pour des valeurs données de n, P et α*, Minitab calcule également la marge d'erreur qui satisfait les conditions ci-dessus à l'aide d'un algorithme itératif, puis calcule l'intervalle associé au pourcentage maximal de la population dans l'intervalle à l'aide de la formule suivante.
P* = P + ε
Pour plus d'informations, reportez-vous à l'ouvrage de Hahn et Meeker1.
Notation
| Terme | Description |
|---|---|
| 1 - α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| P* | pourcentage maximal de la population dans l'intervalle |
| ε | marge d'erreur de l'intervalle de tolérance |
| α* | probabilité de la marge d'erreur de l'intervalle de tolérance |
| n | nombre d'observations dans l'échantillon |
- Hahn, G. J. and Meeker, W. Q. (1991), Statistical Intervals: A Guide for Practitioners. John Wiley & Sons, 170.
