Sur ce thème
Méthodes d'intervalles de tolérance
Minitab calcule les intervalles de tolérance paramétriques et non paramétriques. Les calculs des intervalles de tolérance paramétriques supposent que la distribution parente de l'échantillon soit distribuée de façon normale. Les calculs des intervalles de tolérance non paramétriques supposent uniquement que la distribution parente est continue.
Définitions générales
Soient X 1, X 2, ..., X n les statistiques ordonnées reposant sur un échantillon aléatoire d'effectif n d'une loi de distribution continue.
Soit la fonction de distribution F(x;θ) pour Ω dans un espace de paramètre avec une dimension supérieure ou égale à 1.
Soient L < U deux statistiques basées sur l'échantillon de sorte que pour toutes les valeurs données α et P, avec 0 < α < 1 et 0 < P < 1, la formule suivante est valide pour tous les θ dans Ω :
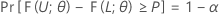
Enfin, l'intervalle [L, U] est un intervalle de tolérance bilatéral avec un contenu égal à P x 100 % et un niveau de confiance égal à 100(1 – α) %. Cet intervalle peut être appelé intervalle de tolérance bilatéral (1 – α, P). Par exemple, si α = 0,10 et que P = 0,85, l'intervalle obtenu est appelé intervalle de tolérance bilatéral (90 %, 0,85).
Si L = –∞ et U < +∞,l'intervalle (-∞, U] est appelé borne de tolérance supérieure unilatérale (1 – α, P). Si L > -∞ et U = +∞, l'intervalle [L, +∞) est appelé borne de tolérance inférieure unilatérale (1 – α, P).
- Une borne de tolérance inférieure unilatérale (1 – α, P) est également une borne de tolérance supérieure unilatérale (α, 1 – P).
- Une borne de confiance inférieure unilatérale (1 – α )100 % du (1 – P)ème percentile de la distribution des données est également une borne de tolérance inférieure unilatérale (1 – α, P). De même, une borne de confiance supérieure unilatérale (1 – α )100 % du P e percentile de la distribution des données est également une borne de tolérance supérieure unilatérale (1 – α , P).
- Si L et U sont des bornes de tolérance inférieure et supérieure unilatérales (1 – α/2 , (1 + P )/2), alors [ L, U ] est une intervalle de tolérance bilatéral approximatif (1 – α, P). Cette méthode peut être utilisée lorsqu'il est impossible d'obtenir directement des intervalles de tolérance bilatéraux. Les intervalles de tolérance bilatéraux qui en résultent sont généralement conservateurs. Voir Guenther1 et Hahn et Meeker2.
- Guenther, W. Montgomery (2004). (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. et Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Intervalles de tolérance exacts pour les lois normales
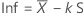

Facteur de tolérance pour des intervalles unilatéraux
Le facteur de tolérance exact pour un intervalle unilatéral est indiqué par l'équation suivante :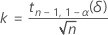
où tn-1,1-α(δ) est le percentile 1 – α de la loi T non centrée avec n – 1 degré de liberté et le paramètre de non-centralité, δ, qui est fourni par la formule suivante :

Facteur de tolérance pour des intervalles bilatéraux
Le facteur de tolérance exact pour un intervalle bilatéral est obtenu en résolvant l'équation suivante pour k. Consultez l'ouvrage de Krishnamoorthy et Mathew1.
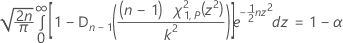
où Fn – 1 est la fonction de répartition pour une loi du Khi deux avec n – 1 degrés de liberté, et où χ21,p est le Pe percentile de la loi du Khi deux non centrée avec 1 degré de liberté et le paramètre de non-centralité z2. La partie gauche de l'équation peut être réécrite comme suit :
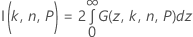
où :
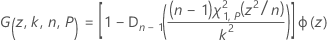
où Φ(z) représente la fonction de densité de probabilité de la loi normale standard. Minitab utilise une quadrature à 16 points de Gauss-Laguerre pour évaluer I(k, n, P).
Notation
| Terme | Description |
|---|---|
| 1 - α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| L | limite inférieure de l'intervalle de tolérance |
| U | limite supérieure de l'intervalle de tolérance |
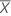 | moyenne de l'échantillon |
| k | facteur de tolérance (également appelé facteur k) |
| S | écart type de l'échantillon |
| n | nombre d'observations dans l'échantillon |
| ZP | Pe percentile de la loi normale standard |
- Krishnamoorthy, K. et Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Intervalles de tolérance non paramétriques exacts pour les distributions continues
Minitab calcule les intervalles de tolérance non paramétriques exacts (1 – α, P), où 1 – α représente le niveau de confiance et P représente la couverture (pourcentage minimal cible de la population dans l'intervalle). La méthode non paramétrique pour les intervalles de tolérance est une méthode sans loi de distribution. Cela signifie que l'intervalle de tolérance non paramétrique ne dépend pas de la population parent de l'échantillon. Minitab utilise une méthode exacte à la fois pour les intervalles unilatéraux et bilatéraux.
Soient X 1, X 2 , ... , X n les statistiques ordonnées reposant sur un échantillon aléatoire d'une population distribuée de façon continue F(x;θ). D'après les conclusions de Wilks1, 2 et de Robbins3, il est possible de démontrer ce qui suit :

où B représente la fonction de répartition de la distribution bêta avec les paramètres a = r et b = n – s + 1. Ainsi, ( Xr , Xs ) est un intervalle de tolérance sans distribution car la couverture de l'intervalle présente une distribution bêta avec des valeurs de paramètres connues, qui sont indépendantes de la distribution de la population parente, F(x;θ).
Intervalles unilatéraux
Soit k l'entier le plus grand remplissant la condition suivante :

où Y est une variable aléatoire binomiale avec les paramètres n et 1 – P. Il est possible de démontrer (voir Krishnamoorthy et Mathew4) qu'une borne de tolérance inférieure unilatérale (1 – α, P) est donnée par Xk . De même, une borne de tolérance supérieure unilatérale (1 – α, P) est exprimée par X n - k +1. Dans les deux cas, la couverture réelle ou effective est exprimée par P(Y > k).
Intervalles bilatéraux
Soit k l'entier le plus petit remplissant la condition suivante :

où V est une variable aléatoire binomiale avec les paramètres n et P. Ainsi,
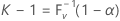
où F V -1(x) représente la fonction de répartition inverse de V. Il est possible de démontrer (voir Krishnamoorthy et Mathew4) qu'un intervalle de tolérance bilatéral (1 – α, P) peut être donné par ( Xr , Xs ). Minitab choisit s = n - r + 1 de sorte que r = ( n – k + 1) / 2. Les deux valeurs r et s sont arrondies à l'entier le plus proche. La couverture réelle ou effective est exprimée par P(V < k – 1).
Notation
| Terme | Description |
|---|---|
| 1 – α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| n | nombre d'observations dans l'échantillon |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. et Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
