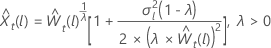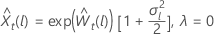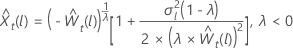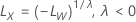Prévision avec le meilleur modèle ARIMA compare de nombreux modèles et sélectionne un modèle final avec un critère dans les spécifications de l’analyse. Pour plus d’informations sur les résultats du modèle ARIMA final, reportez-vous à la Méthodes et formules pour la fonction ARIMAsection . Les sections suivantes contiennent des détails propres à Prévision avec le meilleur modèle ARIMA.
Sélection de modèle
La sélection du modèle s’effectue comme suit :
- Estimez les paramètres du modèle pour chaque modèle. Si un modèle inclut une constante et que l’estimation des paramètres échoue, essayez d’estimer les paramètres sans le terme constant.
- Calculez le critère d’information pour chaque modèle. Le critère par défaut est le critère d’information Akaike corrigé (AICc).
- Produire des résultats pour le modèle avec la meilleure valeur du critère d’information.
Les sections suivantes décrivent les détails qui diffèrent dans la sélection des modèles non saisonniers et saisonniers.
Modèles non saisonniers
- Lorsque vous ajustez des modèles avec un terme constant, les modèles candidats ont p + q ≤ 9.
- Lorsque vous ajustez des modèles sans terme constant, les modèles candidats ont p + q ≤ 10.
- Les modèles avec d = 2 n’incluent jamais de terme constant.
- Le modèle évalue ARIMA(0, d, 0) uniquement lorsque d = 1.
Modèles saisonniers
- Lorsque vous ajustez des modèles avec un terme constant, les modèles candidats ont p + q + P + Q ≤ 9.
- Lorsque vous ajustez des modèles sans terme constant, les modèles candidats ont p + q + P + Q ≤ 10.
- Les modèles avec d + D > 1 n’incluent jamais de terme constant.
- La recherche d’un modèle saisonnier nécessite l’ordre d’au moins un des paramètres saisonniers pour pouvoir être supérieur à 0. La recherche inclut les modèles non saisonniers si les spécifications de la recherche incluent des modèles où tous les paramètres saisonniers ont des ordres de 0.
- Au moins 1 de p, q, P et Q est non nul dans chaque modèle.
Critères
- Critère d'information d'Akaike (AIC)
- Critère d’information Akaike corrigé (AICc)
- Critère d’information Bayésien (BIC)
Le calcul des critères d’information d’un modèle utilise la valeur log-vraisemblance du modèle. Le calcul de la valeur log-vraisemblance utilise un algorithme récursif. Pour de plus amples renseignements, voir la section 8.6 de Brockwell & Davis (1991)1.
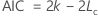
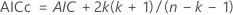
Notation
| Terme | Description |
|---|---|
| k | Le nombre de paramètres dans le modèle
|
| Lc | log de vraisemblance du modèle actuel |
| n | la taille de l’échantillon de la série chronologique |
Transformation de Box-Cox
L’analyse permet une transformation Box-Cox des données. La transformation des données se produit avant la sélection du modèle. Pour plus d’informations sur la transformation box-cox pour les données de séries chronologiques, reportez-vous à la Méthodes et formules pour Transformation de Box-Cox pour série chronologiquesection .
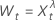pour λ > 0
pour λ = 0
pour λ < 0
où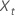 
est la tième valeur de la série chronologique originale et t = 1, ..., n.
Soit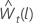 
être la lème valeur de prévision à partir de l’origine, t, pour les données transformées. Soit 
être la variance de prévision l-stepà partir des données transformées. Ensuite, la lème valeur de prévision de t pour la série originale dépend de la valeur de λ:
où 
est la limite dans l’échelle d’origine et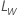 
est la limite dans l’échelle transformée.
Modèle de marche aléatoire
Le modèle ARIMA(0, 1, 0), avec ou sans terme constant, est le modèle de marche aléatoire. Dans Minitab Statistical Software, Prévision avec le meilleur modèle ARIMA s’adapte au modèle de marche aléatoire. La commande nécessite au moins un paramètre de moyenne mobile ou autorégressif. Les limites d’estimation et de probabilité pour le modèle de marche aléatoire ont des formes spécifiques. Les calculs pour la correspondance, les limites de prévision et les limites de probabilité pour les prévisions dépendent du fait que le modèle inclut ou non un terme constant.
Définitions
| Terme | Description |
|---|---|
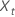 | les observations pour une série chronologique avec t = 1, ..., n |
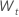 | les premières données différenciées de la série chronologique originale,  |
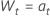
ou
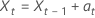
où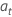 
sont distribués indépendamment et de manière identique et suivent la loi normale avec une moyenne 0 et une variance σ2, t = 2, ..., n.
Les équations qui représentent le modèle avec une constante sont similaires :
ou
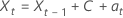
Modèle sans terme constant
La log de vraisemblance a la forme suivante:
Log de vraisemblance
où
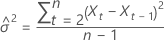
Limite de probabilité de 100 × (1 à α) pour la valeur prévue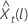 
se présente sous la forme suivante :
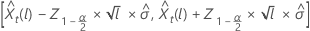
où 
représente le 100 × (1 – α/2)centile de la loi normale standard.
Modèle avec un terme constant
Pour un modèle avec une constante, les calculs de la loglikelihood nécessitent l’estimation de la constante, C. Tout d’abord, différencier les données de la série originale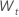 
pour t = 2, ..., n. La constante est la moyenne de l’échantillon de 
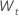et se présente sous la forme suivante :
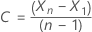
La log de vraisemblance a la forme suivante:
Log de vraisemblance
où
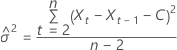
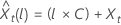
Limite de probabilité de 100 × (1 à α) pour la valeur prévue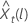 
se présente sous la forme suivante :
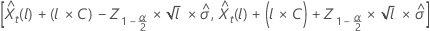
où 
représente le 100 × (1 – α/2)centile de la loi normale standard.
