Sur ce thème
Coefficients
Les coefficients sont estimés à l'aide d'un algorithme itératif qui calcule les estimations par la méthode des moindres carrés. A chaque itération, les prévisions rétrospectives sont calculées, tout comme la SCE. Pour plus de détails, reportez-vous à Box et Jenkins1.
L'algorithme ARIMA est basé sur le programme d'ajustement du logiciel TSERIES écrit par le Professeur William Q. Meeker, Jr., de l'Iowa State University2. Nous sommes reconnaissants au Professeur Meeker pour son aide dans l'adaptation de son programme à Minitab.
Prévisions rétrospectives
Les prévisions rétrospectives sont calculées à l'aide du modèle indiqué et des estimations des paramètres pour l'itération. Pour plus de détails, reportez-vous à Cryer3.
SCE
Formule

Notation
| Terme | Description |
|---|---|
| n | nombre total d'observations |
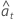 | valeurs résiduelles utilisant les estimations de paramètres de cette itération, prévisions rétrospectives comprises |
SC pour les valeurs résiduelles
Formule
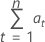
Notation
| Terme | Description |
|---|---|
| n | nombre total d'observations |
| at | valeurs résiduelles utilisant les estimations de paramètres finales, prévisions rétrospectives non comprises |
DL pour les valeurs résiduelles
Formule
Pour un modèle comportant un terme constant :
(n – d) – p – q – 1
Pour un modèle sans terme constant :
(n – d) – p – q
Notation
| Terme | Description |
|---|---|
| n | nombre total d'observations |
| d | nombre de différences |
| p | nombre de paramètres autorégressifs inclus dans le modèle |
| q | nombre de paramètres de moyenne mobile inclus dans le modèle |
CM pour les valeur résiduelles
Formule
Somme des carrés / Degrés de liberté
Statistique du Khi deux
Formule
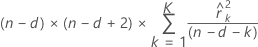
Notation
| Terme | Description |
|---|---|
| n | nombre total d'observations |
| d | nombre de différences |
| K | 12, 24, 36, 48 |
| k | décalage |
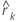 | autocorrélation des valeurs résiduelles pour le ke décalage |
DL pour la statistique du Khi deux
Formule
Pour un modèle comportant un terme constant :
K – p – q – 1
Pour un modèle sans terme constant :
K – p – q
Notation
| Terme | Description |
|---|---|
| K | 12, 24, 36, 48 |
| p | nombre de paramètres autorégressifs inclus dans le modèle |
| q | nombre de paramètres de moyenne mobile inclus dans le modèle |
Valeur de p pour la statistique du Khi deux
Formule
P(X < χ2)
Notation
| Terme | Description |
|---|---|
| X | distribué comme suit : χ2(DL) |
Prévisions
Formule
Les prévisions sont calculées de manière récursive en fonction du modèle et des estimations des paramètres. Par exemple, si un modèle ARIMA est ajusté avec 1 terme autorégressif (AR(1)) et un terme de différenciation saisonnière avec une période de saisonnalité de 12, le modèle suivant est ajusté :
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
Pour déterminer  , la première prévision, où k est l'instant d'origine, trouvez :
, la première prévision, où k est l'instant d'origine, trouvez :
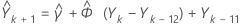
Trouvez ensuite 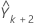 , de la même manière, et ainsi de suite.
, de la même manière, et ainsi de suite.
Pour calculer l'intervalle de prévision à 95 % de la prévision, vous devez d'abord calculer les pondérations.
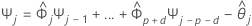
où 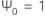 ,
,  pour j < 0 et
pour j < 0 et  pour j > q.
pour j > q.
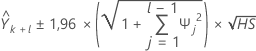
Notation
| Terme | Description |
|---|---|
| Yt | valeur réelle à l'instant t |
| Φ | terme autorégressif |
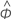 | terme autorégressif estimé |
| γ | terme constant |
| d | nombre de différences |
| p | nombre de paramètres autorégressifs |
| q | nombre de paramètres de moyenne mobile |
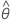 | terme de moyenne mobile estimé |
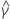 | terme constant estimé |
| CM | carré moyen de l'erreur |
