Sur ce thème
Transformation de Box-Cox
La transformation de Box-Cox est obtenue par la formule suivante :
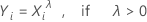
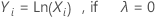

où Xi est une valeur de données d’origine et λ est le paramètre de la transformation. Lorsque l’analyse recherche la valeur optimale de λ, elle arrondit la valeur optimale de λ à 0,5 ou à l’entier le plus proche pour effectuer la transformation.
Valeurs courantes de λ
| λ | Transformation |
|---|---|
| 2 | 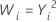 |
| 0,5 |  |
| 0 |  |
| -1 |  |
Recherchez le λ optimal
- Définir le critère pour que la valeur optimale soit un coefficient de variation minimal.
- Divisez la série en sous-séries H .
- Utilisez la méthode de Brent pour trouver la valeur de λ qui minimise le coefficient de variation.
Les sections suivantes définissent la sous-série et le coefficient de variation.
Sous-séries
Divisez les séries en sous-séries par période saisonnière. Si la période saisonnière ne se divise pas uniformément dans la série, omettez les observations restantes du début de la série. Si les spécifications de l’analyse n’incluent pas de période saisonnière, définissez la période saisonnière = 2.
Par exemple, supposons une série chronologique originale avec 10 observations et une période saisonnière de 4 : {5, 6, 3, 2, 9, 8, 1, 7, 10, 4}. Le nombre de sous-séries est 10 modulo 4 = 2. Parce que 4 ne se divise pas uniformément en 10, utilisez uniquement les 8 dernières observations pour former la sous-série. Les sous-séries sont {3, 2, 9, 8} et {1, 7, 10, 4}.
Valeurs manquantes
Si une sous-série contient 1 valeur manquante ou plus, omettez la sous-série des calculs dans la recherche de la valeur optimale de λ. La recherche nécessite au moins 2 sous-séries sans valeurs manquantes.
Coefficient de variation
Utilisez les définitions suivantes pour calculer le coefficient de variation :| Terme | Description |
|---|---|
| X1, X2, ... XN | les observations de la série chronologique originale |
| P | la période saisonnière de la série chronologique originale |
| Xh, i | la ie observation dans la sous-série h, où i=1, ..., P et h=1, ..., H |
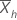 | la moyenne de l’échantillon de la hème sous-série |
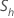 | l’écart-type de l’échantillon de la hème sous-série |
Les équations suivantes définissent les statistiques pour chaque sous-série :
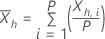
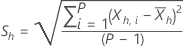
Pour un λ donné et pour h=1, ..., H utilise la définition suivante :
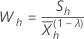
Calculer la moyenne de l’échantillon et l’écart-type de l’échantillon pour les statistiques W :

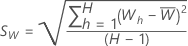

Utilisez la méthode de Brent pour trouver la valeur de λ qui minimise le CV dans l’intervalle à partir des spécifications de l’analyse. L’analyse arrondit la valeur optimale de λ à 0,5 ou à l’entier le plus proche pour effectuer la transformation.
