Sur ce thème
- Analyses disponibles pour les données non normales
- Permet Analyse de capabilité automatisée de sélectionner une méthode
- Exemple d’utilisation Analyse de capabilité automatisée pour sélectionner une méthode
- Utilisation de la fonction Identification de loi individuelle pour trouver une loi ou une transformation appropriée
- Exemple d'utilisation de la fonction Identification de loi individuelle pour comparer les ajustements des lois et des transformations
Analyses disponibles pour les données non normales
- Sélectionnez un modèle de loi non normale qui s'ajuste à vos données, puis analysez les données à l'aide d'une analyse de capabilité pour données non normales, comme Analyse de capabilité utilisant une loi non normale.
- Transformez les données afin que la loi normale devienne un modèle approprié, puis utilisez une analyse de capabilité pour données normales, comme Analyse de capabilité normale.
- Sélectionnez une méthode non paramétrique qui ne fait pas d’hypothèses sur la distribution des données, telle que Analyse de capabilité (non paramétrique).
- Utilisez vos connaissances techniques ou historiques concernant votre procédé.
- Le plus souvent, il est préférable d'utiliser vos connaissances techniques et historiques du procédé pour identifier une loi qui s'ajuste aux données Méthode votre procédé. Par exemple, les données suivent-elles une loi symétrique ? Quelle méthode a fonctionné dans le passé pour des situations similaires?
- Utilisez des évaluations de la qualité de l’ajustement.
- Le test d’Anderson-Darling évalue si une distribution donnée correspond aux données d’un processus. Les diagrammes de probabilité sont un autre outil qui évalue dans quelle mesure les données suivent une distribution.
- Évaluez comment différentes méthodes affectent vos conclusions.
- Si plusieurs méthodes fournissent un ajustement adéquat aux données et des conclusions similaires, alors le choix est moins conséquent. Inversement, si vos conclusions dépendent de la méthode, vous voudrez peut-être rapporter la conclusion la plus conservatrice ou recueillir plus d’informations. Par exemple, vous pouvez utiliser les résultats de distribution de Analyse de capabilité automatisée ou les percentiles de Identification de loi individuelle pour voir comment vos conclusions dépendent de la méthode.
- Si vous prévoyez d’effectuer des analyses de capacité répétées sur votre processus au fil du temps, essayez d’utiliser une méthode susceptible de caractériser correctement votre processus de manière cohérente au fil du temps. L’utilisation de la même méthode vous permet de comparer facilement et directement les indices des analyses répétées.
- Les modèles non normaux et non paramétriques utilisent les unités de données réelles. Le modèle normal d’une transformation utilise des unités transformées.
- Le modèle normal d’une transformation fournit des estimations de la capacité globale et de la capacité du processus.
Utilisez Analyse de capabilité automatisée Minitab Statistical Software pour vous aider à déterminer une méthode raisonnable qui correspond aux données, tout en tenant compte de l’utilité et de la praticité de la méthode. L’analyse considère d’abord les distributions, puis les transformations. Si aucun modèle ne correspond aux données, l’analyse utilise la méthode non paramétrique.
Pour afficher plus de détails sur les données, utilisez Identification de loi individuelle. L’analyse fournit des mesures de qualité d’ajustement pour différentes méthodes afin d’appuyer votre décision quant à la méthode à utiliser.
Permet Analyse de capabilité automatisée de sélectionner une méthode
Permet Analyse de capabilité automatisée d’évaluer la compatibilité de plusieurs méthodes avec les données et de faire un choix raisonnable.
- Sélectionnez .
- Indiquez si vos données sont organisées sur une seule colonne ou sur plusieurs lignes.
- Entrez les limites de spécification pour le processus.
L’analyse considère les distributions, puis les transformations. Si aucune méthode paramétrique ne correspond aux données, l’analyse utilise la méthode non paramétrique. Les résultats comprennent un rapport de capabilité pour la première méthode qui fournit un ajustement raisonnable. Le tableau des résultats de distribution montre l’ordre d’évaluation des méthodes, des informations sur l’ajustement des méthodes et des statistiques de capabilité. Vous pouvez produire des résultats pour une autre méthode afin d’étudier les méthodes plus en détail.
Exemple d’utilisation Analyse de capabilité automatisée pour sélectionner une méthode
Un ingénieur recueille des données sur l’étendue de la déformation des carreaux de céramique. La distribution des données est inconnue, elle effectue Identification de loi individuelle donc sur les données pour déterminer une méthode raisonnable pour une analyse des capabilités.
Le tableau des résultats de distribution montre l’ordre d’évaluation des méthodes. Dans la première ligne, la conclusion du test d’Anderson-Darling est que les données ne suivent pas une distribution normale au niveau de signification de 0,05 parce que la valeur de p est inférieure à 0,05. Dans la deuxième ligne, la conclusion du test d’Anderson-Darling est que la distribution de Weibull est un ajustement raisonnable aux données parce que la valeur de p est supérieure à 0,05. Les résultats de capabilité sont pour la distribution Weibull parce que la distribution Weibull est la première méthode de la liste qui fournit un ajustement raisonnable.
Les ingénieurs utilisent la connaissance des processus pour déterminer si la distribution de Weibull est une méthode raisonnable. Par exemple, la distribution de Weibull a une frontière à 0. Dans les données, 0 est une limite qui représente une mosaïque non déformée.
L’analyse comprend une analyse de capabilité qui utilise la distribution de Weibull.
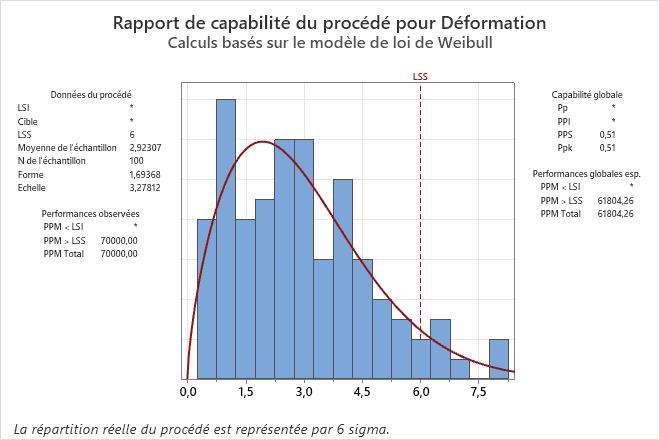
Résultats de la distribution automatisée des capacités : Déformation
| Distribution | Emplacement | Echelle | Seuil | Forme | P | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| Normale | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | 0,5838 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | |||
| Log-normale | 0,8443 | 0,7444 | <0,005 | 0,4242 | |||
| Plus petite valeur extrême | 3,8641 | 1,9924 | <0,01 | 0,5362 | |||
| Plus grande valeur extrême | 2,0958 | 1,4196 | 0,212835 | 0,5130 | |||
| Gamma | 1,2477 | 2,3428 | 0,238337 | 0,4851 | |||
| Logistique | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | |||
| Log-logistique | 0,9097 | 0,4217 | <0,005 | 0,4090 | |||
| Exponentielle | 2,9231 | <0,0025 | 0,3780 | ||||
| Weibull 3 paramètres | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | ||
| Log-normale à 3 paramètres | 1,3788 | 0,4184 | -1,4002 | 0,4961 | |||
| Gamma 3 paramètres | 1,2314 | -0,0197 | 2,3898 | 0,4864 | |||
| Log-logistique 3 paramètres | 1,3043 | 0,2700 | -1,0940 | 0,4656 | |||
| Exponentielle 2 paramètres | 2,6679 | 0,2552 | <0,01 | 0,3982 | |||
| Transformation de Box-Cox | 1,6237 | 0,5380 | 0,574337 | 0,5116 | 0,5214 | ||
| Transformation de Johnson | 0,0112 | 0,9949 | 0,798895 | 0,4959 | |||
| Non paramétrique | 0,6187 |
Utilisation de la fonction Identification de loi individuelle pour trouver une loi ou une transformation appropriée
Utilisez la fonction Identification de loi individuelle avant de réaliser une analyse de capabilité, afin d'identifier la loi ou la transformation la mieux adaptée à vos données. Si aucune distribution ou transformation n’est compatible avec vos données, considérez Analyse de capabilité (non paramétrique).
- Sélectionnez .
- Indiquez si vos données figurent dans une seule colonne ou dans plusieurs lignes.
- Choisissez Utiliser toutes les lois et transformations ou Spécifier choisissez jusqu’à 4 distributions et transformations à tester.
- Analyse de capabilité utilisant une loi non normale
- Analyse de capabilité pour plusieurs variables (loi non normale)
- Analyse Capability Sixpack non normale
- Analyse de capabilité normale
- Analyse Capability Sixpack normale
- Analyse de capabilité normale pour plusieurs variables
- Analyse de capabilité entre/à l'intérieur
Exemple d'utilisation de la fonction Identification de loi individuelle pour comparer les ajustements des lois et des transformations
Un ingénieur recueille des données sur l’étendue de la déformation des carreaux de céramique. La distribution des données étant inconnue, il utilise la fonction Identification de loi individuelle sur les données pour comparer l'adéquation de l'ajustement entre la loi exponentielle et, après application d'une transformation de Johnson, la loi normale.
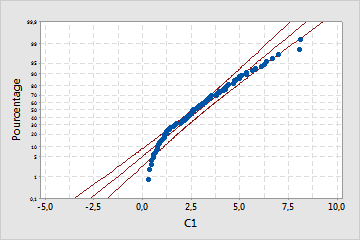
Loi exponentielle
Ce diagramme de probabilité indique que la loi exponentielle n'offre pas un bon ajustement ; la valeur de p est suffisamment petite pour qu'il soit possible de rejeter l'hypothèse nulle selon laquelle les données suivent une loi exponentielle.
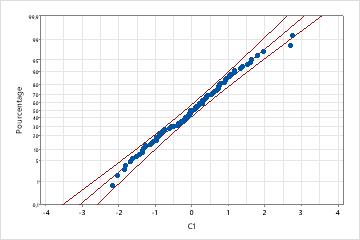
Loi normale avec transformation de Johnson
Toutefois, après l'application d'une transformation de Johnson, les données suivent étroitement une loi normale ; en effet, la valeur de p est élevée et pratiquement tous les points de données se situent à l'intérieur des limites de confiance de la droite de Henry.
