Seleccione el método o la fórmula de su preferencia.
En este tema
- Fórmulas generales para el tamaño de la muestra para los intervalos de tolerancia
- Cálculo del tamaño de la muestra para intervalos de tolerancia normales
- Cálculo del porcentaje máximo de la población en el intervalo para los intervalos de tolerancia normales
- Cálculo del tamaño de la muestra y los porcentajes máximos aceptables de la población en el intervalo para los intervalos de tolerancia no paramétricos
Fórmulas generales para el tamaño de la muestra para los intervalos de tolerancia
Definición de intervalo de tolerancia (bilateral)
Sean X1, X2, ..., Xn los valores ordenados de una muestra aleatoria de tamaño n proveniente de una distribución continua.Sea F(χ,θ) la función de distribución para Ω en algún espacio de parámetro con una dimensión mayor que o igual a 1.
Sean L < U dos estadísticos basados en la muestra tal que para cualquier valor α y P dado, con 0 < α < 1 y 0 < P < 1, se cumpla lo siguiente para cada θ en Ω:
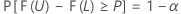
Entonces, el intervalo [ L, U] es un intervalo de tolerancia bilateral con contenido = P x 100% y nivel de confianza = 100(1 - α)%. Tal intervalo se puede denominar un intervalo de tolerancia (1 - α, P) bilateral. Por ejemplo, si α = 0.10 y P = 0.85, entonces el intervalo resultante se denomina un intervalo de tolerancia (90%, 0.85) bilateral.
Tamaño de la muestra y margen de error
Sea C = F( U) – F( L). Un intervalo de tolerancia (1 –α , P) bilateral es tal que: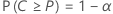
- La probabilidad de que el intervalo abarque al menos 100P% de la población es 1 – α.
- La probabilidad, α*, de que el intervalo abarque más de 100P* % de la población es pequeña, donde P* = P + ε y ε > 0.
En otras palabras, para valores de P, α, ε y α* dados, el tamaño de la muestra se determina de manera que
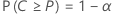
y

Este enfoque se basa en el hecho de que para cualquier P* > P, P( C>P*) es una función decreciente del tamaño de la muestra y, por lo tanto, se puede utilizar para evaluar la precisión.
Elegir un ε y α* pequeños tiene el efecto de reducir el tamaño del intervalo de tolerancia y, por lo tanto, se requiere un tamaño de muestra más grande. Los valores típicos de ε y α* son 0.10, 0.05 o 0.01.
Nota
Las definiciones y los conceptos proporcionados anteriormente también se aplican a los intervalos de tolerancia unilaterales.
- Faulkenberry, G.D. y Weeks, D.L. (1968). Sample size determination for tolerance limits. Technometrics, 10, 343-8.
Cálculo del tamaño de la muestra para intervalos de tolerancia normales
Intervalo unilateral
Faulkenberry y Daly1 muestran que para valores dados de α, P, ε y α*, el tamaño de muestra requerido para un intervalo unilateral se obtiene hallando el valor mínimo para n que satisfaga la siguiente ecuación:

donde la notación tx,y(d) represena el percentil y de una distribución t no central con x grados de libertad y un parámetro de no centralidad d. Los parámetros de no centralidad δ y δ* se calculan de la siguiente manera:

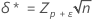
donde zp es el percentil P de la distribución normal estándar.
Minitab utiliza un algoritmo iterativo para hallar el valor mínimo requerido para n.
Intervalo bilateral
Para que los cálculos del tamaño de muestra de un intervalo bilateral se basen en la función I( k, n, P), vaya a Métodos y fórmulas para Intervalos de tolerancia (Distribución normal y haga clic en "Intervalos de tolerancia exactos para distribuciones normales".
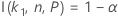
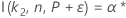
Minitab utiliza un algoritmo iterativo para hallar el valor mínimo requerido para n. Para obtener información adicional, véase Odeh, Chou, y Owen2.
Notación
| Término | Description |
|---|---|
| 1 – α | el nivel de confianza del intervalo de tolerancia |
| P | la cobertura del intervalo de tolerancia (el porcentaje mínimo objetivo de la población en el intervalo) |
| ε | el margen de error del intervalo de tolerancia |
| α* | el margen de probabilidad de error para el intervalo de tolerancia |
| n | el número de observaciones en la muestra |
- Faulkenberry, G.D. y Daly, J.C. (1970). Sample size for tolerance limits on a normal distribution. Technometrics, 12, 813–21.
- Odeh, R. E., Chou, Y.-M. y Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Cálculo del porcentaje máximo de la población en el intervalo para los intervalos de tolerancia normales
P* = P + ε
Los cálculos del margen de error son similares a los cálculos del tamaño de la muestra descritos en Fórmulas generales para el tamaño de la muestra para los intervalos de tolerancia.
Intervalos unilaterales
Para valores dados de n, α, P y α *, el margen de error, ε, para un intervalo unilateral se obtiene resolviendo primero δ* en la siguiente ecuación:
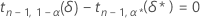
donde la notación tx,y(d) representa el percentil y de una distribución t no central con x grados de libertad y un parámetro de no centralidad d. Minitab utiliza una rutina que busca raíces numéricas para calcular δ*. Después de determinarse el valor de δ*, el valor de ε se puede obtener a partir de la siguiente fórmula:

Intervalos bilaterales
Los cálculos del margen de error de un intervalo bilateral se basan en la función I( k, n, P), que se describe en Intervalos de tolerancia exactos para distribuciones normales.
Para valores dados de n, α, P y α*, el margen de error, ε, para un intervalo bilateral se obtiene utilizando el algoritmo descrito en Odeh, Chou y Owen1. Primero, resuelva la siguiente ecuación para k:
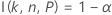

Notación
| Término | Description |
|---|---|
| 1 – α | el nivel de confianza del intervalo de tolerancia |
| P | la cobertura del intervalo de tolerancia (el porcentaje mínimo objetivo de la población en el intervalo) |
| P* | Porcentaje máximo de la población en el intervalo |
| ε | el margen de error del intervalo de tolerancia |
| α* | el margen de probabilidad de error para el intervalo de tolerancia |
| n | el número de observaciones en la muestra |
- Odeh, R. E., Chou, Y.-M. y Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Cálculo del tamaño de la muestra y los porcentajes máximos aceptables de la población en el intervalo para los intervalos de tolerancia no paramétricos
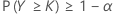
Esto es n – k = FW–1 (1 – α), donde FW–1(.) representa la función de distribución acumulada inversa de W = n – Y.
Del mismo modo, se puede mostrar que un límite de tolerancia superior (1 – α, P) unilateral viene dado por X( n – k + 1 ), donde k satisface las condiciones descritas anteriormente para el límite inferior.
En ambos casos, la cobertura real o efectiva viene dada por P(Y > k).
Además, un intervalo de tolerancia (1 – α, P) bilateral puede expresarse como (Xr, Xs) donde k = s – r es el entero más pequeño que satisface la siguiente condición:
Se ha convertido en una práctica común tomar s = n – r + 1, de modo que r = ( n – k + 1) / 2. Tanto r como s se redondean al entero más cercano. La cobertura real o efectiva viene dada por P( V ≤ k – 1).
Criterio
El criterio para los cálculos de tamaño de la muestra para los intervalos de tolerancia no paramétricos (tanto unilaterales como bilaterales) es similar a los descritos para los datos normales. Más específicamente, para un límite de tolerancia inferior (1 – α, P) unilateral, el criterio consiste en determinar el tamaño de la muestra, n, y el entero más grande k que satisfagan las siguientes condiciones:
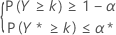
Esta condición es equivalente a encontrar n y el entero más grande k que satisfagan las siguientes condiciones:
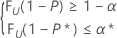
donde FU(.) representa la función de distribución acumulada de una variable aleatoria U que se distribuye como una distribución beta con los parámetros α = k y b = n – k + 1.
Como se señala en Hahn y Meeker1, el criterio produce tamaños de muestra necesarios que son idénticos para los intervalos de tolerancia tanto unilaterales como bilaterales. Por lo tanto, utilizamos el criterio descrito anteriormente para los intervalos de tolerancia tanto unilaterales como bilaterales.
Para los valores dados de ε, P y α*, Minitab utiliza un algoritmo iterativo para encontrar el tamaño mínimo de la muestra que satisfaga las dos condiciones descritas anteriormente. Para los valores dados de n, P y α*, Minitab también calcula el margen de error que satisface las condiciones anteriores utilizando un algoritmo iterativo y luego calcula el intervalo para el porcentaje máximo de la población en el intervalo usando la siguiente fórmula.
P* = P + ε
Para obtener más detalles, véase Hahn y Meeker1.
Notación
| Término | Description |
|---|---|
| 1 - α | el nivel de confianza del intervalo de tolerancia |
| P | la cobertura del intervalo de tolerancia (el porcentaje mínimo objetivo de población en el intervalo) |
| P* | Porcentaje máximo de la población en el intervalo |
| ε | el margen de error del intervalo de tolerancia |
| α* | el margen de probabilidad de error para el intervalo de tolerancia |
| n | el número de observaciones en la muestra |
- Hahn, G. J. y Meeker, W. Q. (1991), Statistical Intervals: A Guide for Practitioners. John Wiley & Sons, 170.
