En este tema
Gráfica de optimización
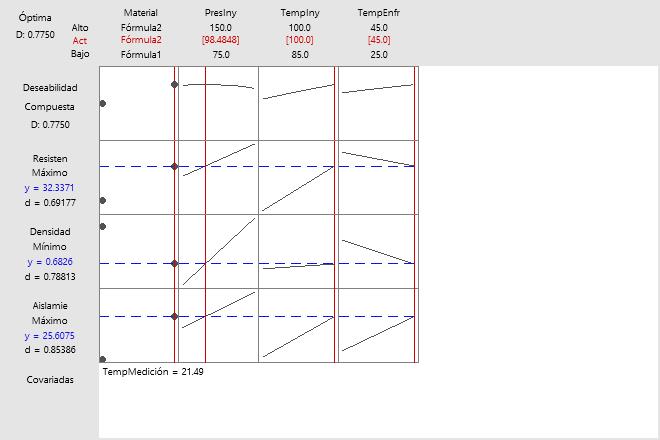
La gráfica de optimización muestra cómo las variables afectan las respuestas pronosticadas. Cuando la gráfica de optimización es interactiva, las celdas muestran cómo la variable de respuesta o la deseabilidad compuesta correspondientes cambian en función de una de las variables, mientras las demás variables permanecen fijas. La gráfica de optimización muestra los valores ajustados para la configuración de los predictores.
- Una columna para cada variable (predictora)
- Las líneas verticales rojas en la gráfica representan la configuración actual.
- Una fila para cada variable de respuesta.
- Las líneas azules horizontales representan los valores de respuesta actuales.
- Deseabilidad compuesta
- En la fila superior y en la esquina superior izquierda está la deseabilidad compuesta (D).
- Barra de herramientas interactiva
- El botón Predecir en la parte superior izquierda de la barra de herramientas calcula la predicción correspondiente a la configuración actual de las variables.
El tipo de valores ajustados que Minitab muestra depende del tipo de variable de respuesta del modelo. Por ejemplo, Minitab muestra medias, probabilidades o desviaciones estándar dependiendo de si tiene mediciones continuas o de recuento, datos binarios o modelos que usan Analizar variabilidad.
- Estadísticas
- Haga doble clic en la gráfica de optimización para hacerla interactiva.
- Módulo de análisis predictivo
- La trama es siempre interactiva.
Interpretación
Utilice la gráfica de optimización para determinar la configuración óptima de los predictores de acuerdo con los parámetros que usted especificó.
- Material: Los dos puntos de cada celda de esta columna representan los dos niveles de la variable categórica: Formula1 y Formula2. Fórmula2 parece ser el mejor material. Si se utiliza Fórmula1, el valor aislante se reduciría y la densidad aumentaría, siendo ambos resultados indeseables. Sin embargo, debido a que el tipo de material interactúa con otros factores, esta tendencia podría no mantenerse con otros valores de configuración. Considere si puede encontrar una solución local para Fórmula1. También puede cambiar la configuración de Fórmula1 directamente en la gráfica moviendo las barras verticales.
- PresIny: Al aumentar la presión de inyección, aumentan las tres respuestas. Por lo tanto, el valor de configuración óptimo se encuentra en la mitad del rango (98.4848), lo que representa un compromiso entre metas opuestas. La meta es maximizar el valor aislante, minimizar la densidad y maximizar la resistencia.
- TempIny: El aumento de la temperatura de inyección también aumenta todas las respuestas. Sin embargo, el efecto sobre la densidad es mínimo en comparación con el efecto sobre el valor aislante. Por lo tanto, usted aumenta la deseabilidad compuesta maximizando la temperatura de inyección. Los valores de configuración óptimos de la temperatura de inyección se encuentran en sus niveles máximos en el experimento. Este resultado sugiere que se debería considerar la posibilidad de experimentar con temperaturas más elevadas.
- TempEnfr: Al aumentar la temperatura de enfriamiento, aumenta el valor aislante, pero se reducen la densidad y la resistencia. Los valores de configuración óptimos para la temperatura de inyección y la temperatura de enfriamiento se encuentran en sus niveles máximos en el experimento. Este resultado sugiere que se debería considerar la posibilidad de experimentar con temperaturas más elevadas. Las gráficas muestran que sería recomendable considerar particularmente el uso de temperaturas de enfriamiento más altas. Si fuera posible extrapolar las gráficas, aumentar las temperaturas de enfriamiento mejoraría el valor aislante y la densidad. Sin embargo, la resistencia disminuiría.
Para un modelo de regresión lineal, examine los intervalos de predicción para determinar si el rango de valores probables para un solo valor futuro se encuentra dentro de los límites aceptables para el proceso. Las regiones grises indican el lugar donde la respuesta correspondiente tiene una deseabilidad de cero.
Parámetros
Minitab muestra los parámetros del diseño para cada respuesta en la tabla Parámetros. Examine estos resultados para verificar que los parámetros del diseño que se muestran sean los correctos.
Los valores que usted elige para meta, inferior, objetivo, superior y ponderación definen la función de deseabilidad para cada respuesta individual. Los parámetros de importancia determinan cómo se combinan las funciones de deseabilidad en una sola deseabilidad compuesta.
- El Optimizador de respuestas menú incluye Estadísticas optimización para múltiples respuestas.
- El Optimizador de respuestas en el Módulo de análisis predictivo incluye optimización para una sola respuesta.
- ¿Cuál meta de optimización de respuesta debo usar?
- Establecimiento de un valor objetivo y bordes superior e inferior en la optimización de respuestas
- Determinación de la ponderación en la optimización de respuestas
- ¿Qué es la importancia en la optimización de respuestas?
- ¿Qué es deseabilidad individual y deseabilidad compuesta?
Interpretación
- La meta para Resistencia es maximizarla. Un valor de 38.1821 se considera excelente, mientras que valores por debajo de 19.2189 son inaceptables.
- La meta para Densidad es minimizarla. Un valor de 0.4351 se considera excelente, mientras que valores por encima de 1.60314 son inaceptables.
- La meta para Aislamiento es maximizarlo. Un valor de 27.7156 se considera excelente, mientras que valores por debajo de 13.2905 son inaceptables.
Las tres respuestas tienen el mismo valor de importancia. Por lo tanto, las tres respuestas tienen igual influencia sobre la deseabilidad compuesta.
Predicción de respuesta múltiple
| Variable | Valor de configuración |
|---|---|
| Material | Fórmula2 |
| PresIny | 98.4848 |
| TempIny | 100 |
| TempEnfr | 45 |
| TempMedición | 21.4875 |
| Respuesta | Ajuste | EE de ajuste | IC de 95% | IP de 95% |
|---|---|---|---|---|
| Resistencia | 32.34 | 1.04 | (29.45, 35.22) | (27.25, 37.43) |
| Densidad | 0.6826 | 0.0597 | (0.5167, 0.8484) | (0.3899, 0.9753) |
| Aislamiento | 25.608 | 0.268 | (24.863, 26.352) | (24.294, 26.921) |
Predicción de respuesta
Minitab utiliza la configuración de las variables especificada en esta tabla para calcular los ajustes para todas las respuestas que se incluyen en el procedimiento de optimización.
- El Optimizador de respuestas menú incluye Estadísticas optimización para múltiples respuestas.
- El Optimizador de respuestas en el Módulo de análisis predictivo incluye optimización para una sola respuesta.
Cuando se ejecuta Optimizador de respuestas por primera vez, la tabla de predicción de respuesta múltiple muestra los valores óptimos que identifica el algoritmo. Si cambia la configuración de variables en la gráfica y hace clic en el Predecir botón de la barra de herramientas, Minitab crea una tabla con la nueva configuración.
Utilice esta tabla para verificar que el análisis se realizó tal como estaba previsto.
Ajuste
Los valores ajustados también se denominan ajustes o  . Los valores ajustados son estimaciones de punto de la respuesta media para valores específicos de los predictores. Los valores de los predictores también se denominan valores de X. Minitab utiliza la ecuación de regresión y la configuración de las variables para calcular el ajuste.
. Los valores ajustados son estimaciones de punto de la respuesta media para valores específicos de los predictores. Los valores de los predictores también se denominan valores de X. Minitab utiliza la ecuación de regresión y la configuración de las variables para calcular el ajuste.
El tipo de valores ajustados que Minitab muestra depende del tipo de variable de respuesta del modelo. Por ejemplo, Minitab muestra las medias, las probabilidades o las desviaciones estándar dependiendo de si usted tiene mediciones continuas o de conteos, datos binarios o modelos que utilizan Analizar variabilidad.
Interpretación
Los valores ajustados se calculan ingresando valores de X en la ecuación del modelo para una variable de respuesta.
Por ejemplo, si la ecuación es y = 5 + 10x, el valor ajustado para el valor de X, 2, es 25 (25 = 5 + 10(2)).
EE de ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la respuesta media estimada para la configuración especificada de las variables. El cálculo del intervalo de confianza para la respuesta media utiliza el error estándar del ajuste. Los errores estándar son siempre no negativos. El análisis calcula los errores estándar para los modelos desde el Estadísticas menú y los modelos desde Regresión lineal y Regresión logística binaria desde el Módulo de análisis predictivo archivo .
Interpretación
Utilice el error estándar del ajuste para medir la precisión de la estimación de la respuesta media. Cuanto menor sea el error estándar, más precisa será la respuesta media pronosticada. Por ejemplo, un analista desarrolla un modelo para pronosticar el tiempo de entrega. Para un conjunto de valores de configuración de las variables, el modelo predice un tiempo medio de entrega de 3.80 días. El error estándar del ajuste para esta configuración es 0.08 días. Para un segundo conjunto de valores de configuración de las variables, el modelo produce el mismo tiempo medio de entrega con un error estándar del ajuste de 0.02 días. El analista puede estar más seguro de que el tiempo medio de entrega del segundo conjunto de valores de configuración de las variables es cercano a 3.80 días.
Con el valor ajustado, usted puede utilizar el error estándar del ajuste para crear un intervalo de confianza para la respuesta media. Por ejemplo, dependiendo del número de grados de libertad, un intervalo de confianza de 95% se extiende aproximadamente dos errores estándar por encima y por debajo de la media pronosticada. Para los tiempos de entrega, el intervalo de confianza de 95% de la media pronosticada de 3.80 días cuando el error estándar es 0.08 es (3.64, 3.96) días. Puede estar 95% seguro de que la media de la población se encuentra dentro de este rango. Cuando el error estándar es 0.02, el intervalo de confianza de 95% es (3.76, 3.84) días. El intervalo de confianza del segundo conjunto de valores de configuración de las variables es más estrecho porque el error estándar es menor.
IC de 95%
El intervalo de confianza para el ajuste proporciona un rango de valores probables para la respuesta media dada la configuración especificada de los predictores. El análisis calcula los intervalos de confianza para los modelos desde el Estadísticas menú y los modelos desde Regresión lineal y Regresión logística binaria desde el Módulo de análisis predictivoarchivo .
Interpretación
Utilice el intervalo de confianza para evaluar la estimación del valor ajustado para los valores observados de las variables.
Por ejemplo, con un nivel de confianza de 95%, puede estar 95% seguro de que el intervalo de confianza contiene la media de la población para los valores especificados de las variables incluidas en el modelo. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Un intervalo de confianza amplio indica que usted puede estar menos seguro con respecto a la media de los valores futuros. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
IP de 95%
El intervalo de predicción es un rango que es probable que contenga una respuesta futura individual para una combinación seleccionada de valores de configuración de las variables. El análisis calcula los intervalos de predicción para los modelos desde el Estadísticas menú y los modelos desde Regresión lineal el Módulo de análisis predictivo archivo .
Interpretación
Utilice los intervalos de predicción (PI) para evaluar la precisión de las predicciones.Los intervalos de predicción ayudan a evaluar la importancia práctica de los resultados.Si un intervalo de predicción se extiende más allá de los límites aceptables, es posible que las predicciones no sean lo suficientemente precisas para sus requerimientos.
Con un IP de 95%, puede estar 95% seguro de que una respuesta individual estará contenida en el intervalo dada la configuración de los predictores que se especificó. El intervalo de predicción es siempre más amplio que el intervalo de confianza debido a la incertidumbre adicional que implica predecir una sola respuesta frente a la respuesta media.
Por ejemplo, un ingeniero de materiales que trabaja en una fábrica de muebles desarrolla un modelo de regresión simple para predecir la rigidez del tablero de partículas a partir de la densidad del tablero. El ingeniero verifica que el modelo cumple con los supuestos del análisis. Luego, el analista utiliza el modelo para predecir la rigidez.
La ecuación de regresión predice que la rigidez para una nueva observación con una densidad de 25 es -21.53 + 3.541*25, o 66.995. Aunque es poco probable que dicha observación tenga una rigidez de 66.995 exactamente, el intervalo de predicción indica que el ingeniero puede estar 95% seguro de que el valor real estará entre 48 y 86 aproximadamente..
Deseabilidad compuesta
Utilice la deseabilidad compuesta para evaluar qué tan bien la configuración optimiza un conjunto de respuestas en general. La deseabilidad tiene un rango de cero a uno. Uno representa la situación ideal; cero indica que una o más respuestas están fuera de los límites aceptables.
- El Optimizador de respuestas menú incluye Estadísticas optimización para múltiples respuestas.
- El Optimizador de respuestas en el Módulo de análisis predictivo incluye optimización para una sola respuesta.
Con frecuencia, si usted tiene múltiples respuestas, no existe una configuración de factores que maximice simultáneamente la deseabilidad de todas las respuestas. Por esa razón, Minitab maximiza la deseabilidad compuesta. La deseabilidad compuesta combina la deseabilidad individual de todas las variables de respuesta en una sola medida. Se hace más énfasis en las variables de respuesta con la mayor importancia.
Para obtener más información, lea ¿Qué es deseabilidad individual y deseabilidad compuesta?.
Interpretación
Los valores de deseabilidad compuesta que están cerca de 1 indican que la configuración alcanza resultados favorables para todas las respuestas.
