Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
Un equipo de investigadores recopila y publica información detallada sobre los factores que afectan las enfermedades cardíacas. Las variables incluyen edad, sexo, niveles de colesterol, frecuencia cardíaca máxima, y más. Este ejemplo se basa en un conjunto de datos públicos que proporciona información detallada sobre las enfermedades cardíacas. Los datos originales son de archive.ics.uci.edu.
Después de la exploración inicial para Clasificación CART® identificar los predictores importantes, los investigadores utilizan ambos Clasificación TreeNet® y Clasificación Random Forests® crean modelos más intensivos a partir del mismo conjunto de datos. Los investigadores comparan la tabla de resumen del modelo y la gráfica ROC de los resultados para evaluar qué modelo proporciona un mejor resultado de predicción. Para los resultados de los otros análisis, vaya a Ejemplo de Clasificación CART® y a Ejemplo de Clasificación Random Forests®.
- Abra los datos de muestra, EnfermedadesDelCorazonBinario.MWX.
- Elija .
- En la lista desplegable, seleccione Respuesta binaria.
- En Respuesta, ingrese 'Enfermedad cardíaca'.
- En Response event, seleccione Sí para indicar que se ha identificado una enfermedad cardíaca en el paciente.
- En Predictores continuos, escriba Edad, 'Descansar la presión arterial', Colesterol, 'Frecuencia cardíaca máxima', y 'Old Peak'.
- En Predictores categóricos, escriba Sexo, 'Tipo de dolor torácico', 'Azúcar en la sangre en ayunas', 'Rest ECG', 'Ejercicio Angina', Pendiente, 'Buques principales', y Thal.
- Haga clic en Aceptar.
Interpretar los resultados
Para este análisis, Minitab cultiva 300 árboles y el número óptimo de árboles es 298. Debido a que el número óptimo de árboles está cerca del número máximo de árboles que crece el modelo, los investigadores repiten el análisis con más árboles.
Resumen del modelo
| Total de predictores | 13 |
|---|---|
| Predictores importantes | 13 |
| Número de árboles cultivados | 300 |
| Número óptimo de árboles | 298 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| Logverosimilitud promedio | 0.2556 | 0.3881 |
| Área bajo la curva ROC | 0.9796 | 0.9089 |
| IC de 95% | (0.9664, 0.9929) | (0.8759, 0.9419) |
| Elevación | 2.1799 | 2.1087 |
| Tasa de clasificación errónea | 0.0891 | 0.1617 |
Ejemplo con 500 árboles
- Seleccione Ajustar hiperparámetros en los resultados.
- En Número de árboles, ingrese 500.
- Haga clic en Mostrar resultados.
Interpretar los resultados
Para este análisis, hubo 500 árboles cultivados y el número óptimo de árboles es 351. El mejor modelo utiliza una tasa de aprendizaje de 0,01, utiliza una fracción de submuestra de 0,5 y utiliza 6 como número máximo de nodos terminales.
Método
| Criterio para seleccionar un número óptimo de árboles | Máxima logverosimilitud |
|---|---|
| Validación del modelo | Validación cruzada de 5 pliegues |
| Tasa de aprendizaje | 0.01 |
| Método de selección de submuestras | Completamente aleatorio |
| Fracción de submuestra | 0.5 |
| Máximo de nodos terminales por árbol | 6 |
| Tamaño mínimo del nodo terminal | 3 |
| Número de predictores seleccionados para la división de nodos | Número total de predictores = 13 |
| Filas utilizadas | 303 |
Información de respuesta binaria
| Variable | Clase | Conteo | % |
|---|---|---|---|
| Enfermedad cardíaca | Sí (Evento) | 139 | 45.87 |
| No | 164 | 54.13 | |
| Todo | 303 | 100.00 |
Método
| Criterio para seleccionar un número óptimo de árboles | Máxima logverosimilitud |
|---|---|
| Validación del modelo | Validación cruzada de 5 pliegues |
| Tasa de aprendizaje | 0.001, 0.01, 0.1 |
| Fracción de submuestra | 0.5, 0.7 |
| Máximo de nodos terminales por árbol | 6 |
| Tamaño mínimo del nodo terminal | 3 |
| Número de predictores seleccionados para la división de nodos | Número total de predictores = 13 |
| Filas utilizadas | 303 |
Información de respuesta binaria
| Variable | Clase | Conteo | % |
|---|---|---|---|
| Enfermedad cardíaca | Sí (Evento) | 139 | 45.87 |
| No | 164 | 54.13 | |
| Todo | 303 | 100.00 |
Optimización de hiperparámetros
| Modelo | Número óptimo de árboles | Log-verosimilitud promedio | Área bajo la curva ROC | Tasa de clasificación errónea | Tasa de aprendizaje | Fracción de submuestra |
|---|---|---|---|---|---|---|
| 1 | 500 | 0.542902 | 0.902956 | 0.171749 | 0.001 | 0.5 |
| 2* | 351 | 0.386536 | 0.908920 | 0.175027 | 0.010 | 0.5 |
| 3 | 33 | 0.396555 | 0.900782 | 0.161694 | 0.100 | 0.5 |
| 4 | 500 | 0.543292 | 0.894178 | 0.178142 | 0.001 | 0.7 |
| 5 | 374 | 0.389607 | 0.906620 | 0.165082 | 0.010 | 0.7 |
| 6 | 39 | 0.393382 | 0.901399 | 0.174973 | 0.100 | 0.7 |
| Modelo | Máximo de nodos terminales |
|---|---|
| 1 | 6 |
| 2* | 6 |
| 3 | 6 |
| 4 | 6 |
| 5 | 6 |
| 6 | 6 |
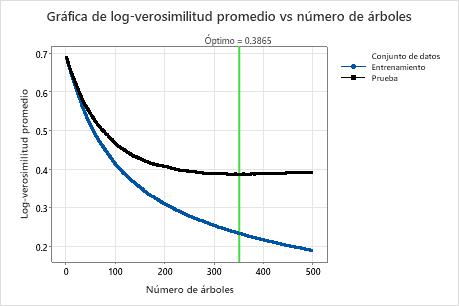
La gráfica de log-verosimilitud promedio vs número de árboles muestra toda la curva sobre el número de árboles crecidos. El valor óptimo para los datos de prueba es 0.3865 cuando el número de árboles es 351.
Resumen del modelo
| Total de predictores | 13 |
|---|---|
| Predictores importantes | 13 |
| Número de árboles cultivados | 500 |
| Número óptimo de árboles | 351 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| Logverosimilitud promedio | 0.2341 | 0.3865 |
| Área bajo la curva ROC | 0.9825 | 0.9089 |
| IC de 95% | (0.9706, 0.9945) | (0.8757, 0.9421) |
| Elevación | 2.1799 | 2.1087 |
| Tasa de clasificación errónea | 0.0759 | 0.1750 |
Resumen del modelo
| Total de predictores | 13 |
|---|---|
| Predictores importantes | 13 |
| Estadísticas | Out-of-Bag |
|---|---|
| Logverosimilitud promedio | 0.4004 |
| Área bajo la curva ROC | 0.9028 |
| IC de 95% | (0.8693, 0.9363) |
| Elevación | 2.1079 |
| Tasa de clasificación errónea | 0.1848 |
La tabla de resumen del modelo muestra que la probabilidad logarítmica negativa media cuando el número de árboles es 351 es de aproximadamente 0,23 para los datos de entrenamiento y de aproximadamente 0,39 para los datos de prueba. Estas estadísticas indican un modelo similar al que crea Minitab Random Forests®. Además, las tasas de clasificaciones erróneas son similares.
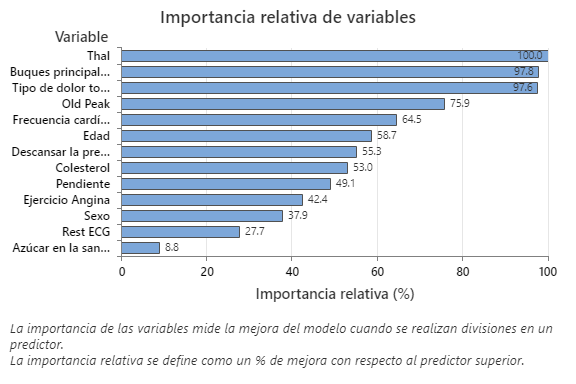
La gráfica Importancia relativa de las variables presenta los predictores en el orden de su efecto en la mejora del modelo cuando se realizan divisiones en un predictor sobre la secuencia de árboles. La variable predictora más importante es Thal. Si la contribución de la variable predictora más importante, Thal, es 100%, entonces la siguiente variable importante, Vasos principales, tiene una contribución de 97.8%. Esto significa que Vasos principales es 97.8% tan importante como Thal en este modelo de clasificación.
Matriz de confusión
| Clase de predicción (entrenamiento) | Clase de predicción (prueba) | ||||||
|---|---|---|---|---|---|---|---|
| Clase real | Conteo | Sí | No | % Correcto | Sí | No | % Correcto |
| Sí (Evento) | 139 | 124 | 15 | 89.21 | 110 | 29 | 79.14 |
| No | 164 | 8 | 156 | 95.12 | 24 | 140 | 85.37 |
| Todo | 303 | 132 | 171 | 92.41 | 134 | 169 | 82.51 |
| Estadísticas | Entrenamiento (%) | Prueba (%) |
|---|---|---|
| Tasa de positivos verdaderos (sensibilidad o potencia) | 89.21 | 79.14 |
| Tasa de positivos falsos (error tipo I) | 4.88 | 14.63 |
| Tasa de negativos falsos (error tipo II) | 10.79 | 20.86 |
| Tasa de negativos verdaderos (especificidad) | 95.12 | 85.37 |
La matriz de confusión muestra qué tan efectivo es el modelo para separar las clases correctamente. En este ejemplo, la probabilidad de que un evento sea pronosticado correctamente es 79.14%. La probabilidad de que un no evento se pronosticado correctamente es 85.37%.
Clasificación errónea
| Entrenamiento | Prueba | ||||
|---|---|---|---|---|---|
| Clasificado erróneamente | % Error | Clasificado erróneamente | % Error | ||
| Clase real | Conteo | ||||
| Sí (Evento) | 139 | 15 | 10.79 | 29 | 20.86 |
| No | 164 | 8 | 4.88 | 24 | 14.63 |
| Todo | 303 | 23 | 7.59 | 53 | 17.49 |
La tasa de clasificaciones erróneas ayuda a indicar si el modelo predecirá nuevas observaciones con exactitud. Para la predicción de eventos, el error de clasificaciones erróneas de prueba es 20.86%. Para la predicción de no eventos, el error de clasificaciones erróneas es 14.63% y, en general, el error de clasificaciones erróneas es 17.49%.
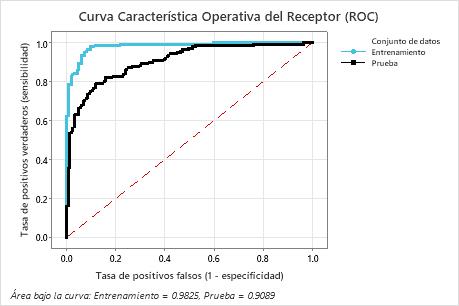
El área bajo de la curva ROC, cuando el número de árboles es 351, es aproximadamente 0.98 para los datos de entrenamiento y aproximadamente 0.91 para los datos de prueba. Esto muestra una buena mejora con respecto al Clasificación CART® modelo . El Clasificación Random Forests® modelo tiene un AUROC de prueba de 0.9028, por lo que estos 2 métodos dan resultados similares.
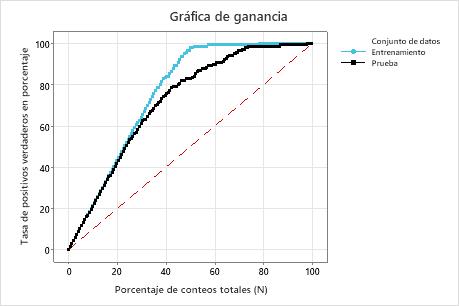
En este ejemplo, la gráfica de ganancia muestra un fuerte aumento por encima de la línea de referencia y, luego, un aplanamiento. En este caso, aproximadamente 40% de los datos representan aproximadamente 80% de los verdaderos positivos. Esta diferencia es la ganancia adicional que se obtiene al utilizar el modelo.
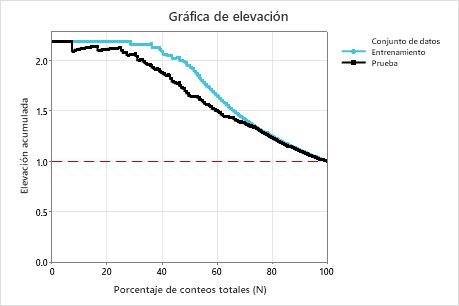
En este ejemplo, la gráfica de elevación muestra un gran aumento por encima de la línea de referencia que disminuye gradualmente.
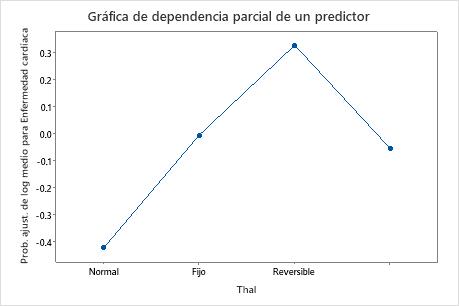
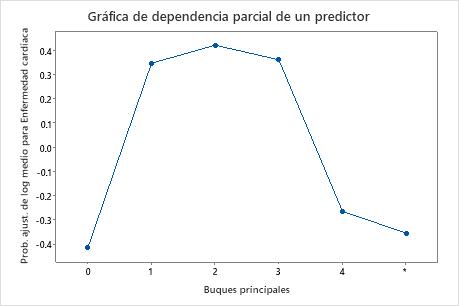
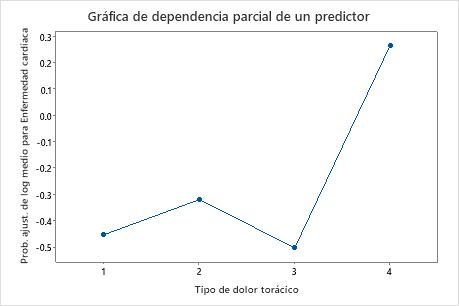
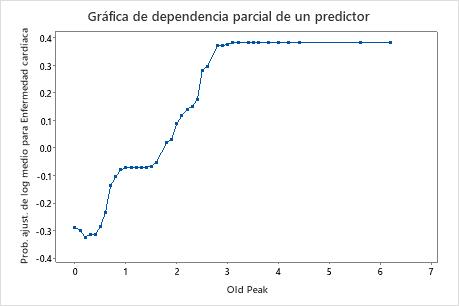
Utilice las gráficas de dependencia parcial para obtener información sobre cómo las variables o pares de variables importantes afectan los valores de respuesta ajustados. Los valores de respuesta ajustados están se encuentran en la escala semi-logarítmica. Las gráficas de dependencia parcial muestran si la relación entre la respuesta y una variable es lineal, monótona o más compleja.
Por ejemplo, en la gráfica de dependencia parcial del tipo de dolor de pecho, las probabilidades de 1/2 logaritmo varían y luego aumentan abruptamente. Cuando el tipo de dolor de pecho es 4, las probabilidades de 1/2 logaritmo de la incidencia de enfermedad cardíaca aumentan de aproximadamente −0.04 a 0.03. Seleccionar o producir gráficas para otras variables