En este tema
- Paso 1: Determinar cuáles términos tienen el mayor efecto en la respuesta
- Paso 2: Determinar cuáles términos tienen efectos estadísticamente significativos en la respuesta
- Paso 3: Entender los efectos de los predictores
- Paso 4: Determinar hasta qué punto el modelo se ajusta a los datos
- Paso 5: Determinar si el modelo no se ajusta a los datos
Paso 1: Determinar cuáles términos tienen el mayor efecto en la respuesta
Utilice un diagrama de Pareto de los efectos estandarizados para comparar la magnitud relativa y la significancia estadística de los efectos principales, cuadrados y de interacción.
Minitab grafica los efectos estandarizados colocando sus valores absolutos en orden decreciente. La línea de referencia en la gráfica indica cuáles efectos son significativos. Por opción predeterminada, Minitab utiliza un nivel de significancia de 0.05 para dibujar la línea de referencia.
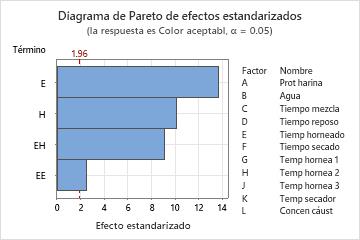
Resultados clave: Diagrama de Pareto
En estos resultados, la gráfica incluye solo términos que están en el modelo. El diagrama muestra que 2 efectos principales son estadísticamente significativos. Un término cuadrático y un efecto de interacción también son estadísticamente significativos.
Además, usted puede ver que el efecto más grande es E porque es el que más se extiende. El efecto del término cuadrático EE es el más pequeño porque es el que menos se extiende.
Paso 2: Determinar cuáles términos tienen efectos estadísticamente significativos en la respuesta
- Valor p ≤ α: La asociación es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que hay una asociación estadísticamente significativa entre la variable de respuesta y el término.
- Valor p > α: La asociación no es estadísticamente significativa
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que existe una asociación estadísticamente significativa entre la variable de respuesta y el término. Le convendría reajustar el modelo sin el término.
- Factores
- Si un coeficiente de un factor es significativo, usted puede concluir que la probabilidad del evento no es la misma para todos los niveles del factor.
- Interacciones entre factores
- Si un coeficiente de un término de interacción es significativo, la relación entre un factor y la respuesta depende del resto de los factores en el término. En este caso, usted no debe interpretar los efectos principales sin considerar el efecto de interacción.
- Términos cuadráticos
- Si un coeficiente de un término cuadrado es significativo, usted puede concluir que la relación entre el factor y la respuesta sigue una línea curva.
- Covariables
- Si el coeficiente de una covariable es estadísticamente significativo, usted puede concluir que la asociación entre la respuesta y la covariable es estadísticamente significativa.
- Bloques
- Si el coeficiente de un bloque es estadísticamente significativo, usted puede concluir que la función de enlace para el bloque es diferente del valor promedio.
Coeficientes codificados
| Término | Coef | EE del coef. | FIV |
|---|---|---|---|
| Constante | 2.394 | 0.145 | |
| Tiemp horneado | 0.7349 | 0.0538 | 1.11 |
| Temp hornea 2 | 0.5451 | 0.0541 | 1.20 |
| Tiemp horneado*Tiemp horneado | -0.384 | 0.153 | 1.04 |
| Tiemp horneado*Temp hornea 2 | -0.5106 | 0.0562 | 1.24 |
Resultados clave: Coeficientes
En estos resultados, los coeficientes de Tiemp horneado y Temp hornea 2 son números positivos. El coeficiente del término cuadrado de Tiemp horneado y el coeficiente del término de interacción entre Tiemp horneado y Temp hornea 2 son números negativos. Por lo general, los coeficientes positivos hacen que el evento sea más probable y los coeficientes negativos hacen que el evento sea menos probable a medida que el valor del término aumenta.
Análisis de Varianza
| Fuente | GL | Desv. ajust. | Media ajust. | Chi-cuadrada | Valor p |
|---|---|---|---|---|---|
| Modelo | 4 | 737.452 | 184.363 | 737.45 | 0.000 |
| Tiemp horneado | 1 | 203.236 | 203.236 | 203.24 | 0.000 |
| Temp hornea 2 | 1 | 100.432 | 100.432 | 100.43 | 0.000 |
| Tiemp horneado*Tiemp horneado | 1 | 6.770 | 6.770 | 6.77 | 0.009 |
| Tiemp horneado*Temp hornea 2 | 1 | 80.605 | 80.605 | 80.61 | 0.000 |
| Error | 45 | 32.276 | 0.717 | ||
| Total | 49 | 769.728 |
Resultados clave: Valor p
En estos resultados, los efectos principales de Tiemp horneado y Temp hornea 2 son estadísticamente significativos en el nivel 0.05. Usted puede concluir que los cambios en estas variables están asociados con los cambios en la variable de respuesta. Debido a que hay términos de orden superior en el modelo, los coeficientes de los efectos principales no describen completamente el efecto de estos factores.
El término cuadrático de Tiemp horneado es significativo. Usted puede concluir que los cambios en esta variable están asociados con los cambios en la variable de respuesta, pero la asociación no es lineal.
El efecto de interacción entre Tiemp horneado y Temp hornea 2 es significativo. Usted puede concluir que el efecto sobre el color de los cambios en Tiemp horneado depende del nivel de Temp hornea 2. De manera equivalente, puede concluir que el efecto sobre el color de los cambios en Temp hornea 2 depende del nivel de Tiemp horneado.
Paso 3: Entender los efectos de los predictores
- Relaciones de probabilidades para predictores continuos
- Las relaciones de probabilidades que son mayores que 1 indican que es más probable que el evento ocurra a medida que aumenta el predictor. Las relaciones de probabilidades que son menores que 1 indican que es menos probable que el evento ocurra a medida que aumenta el predictor.
Relaciones de probabilidades para predictores continuos
Unidad
de
cambioRelación de
probabilidadesIC de 95% Tiemp horneado 2 * (*, *) Temp hornea 2 15 2.1653 (1.9652, 2.3858) Resultado clave: Relación de probabilidades
En estos resultados, el modelo tiene 3 términos para predecir si el color de los pretzels satisface los estándares de calidad: Tiemp horneado, Temp hornea 2 y el término cuadrático de Tiemp horneado. En este ejemplo, un color aceptable es el evento.
La unidad de cambio muestra la diferencia en unidades naturales para una unidad codificada en el diseño. Por ejemplo, en unidades naturales, el nivel bajo de Temp hornea 2 es 127. El nivel alto es 157 grados. La distancia del nivel bajo al punto medio representa un cambio de 1 unidad codificada.. En este caso, esa distancia es 15 grados.
La relación de probabilidades para Temp hornea 2 es aproximadamente 2.17. Por cada 15 grados que la temperatura aumenta, las probabilidades de que el color de un pretzel sea aceptable aumenta en cerca de 2.17 veces.
La relación de probabilidades de Tiemp horneado falta porque el modelo incluye el término cuadrático de Tiemp horneado. La relación de probabilidades no tiene un valor fijo porque el valor depende del valor de Tiemp horneado.
- Relaciones de probabilidades para predictores categóricos
-
Para los predictores categóricos, la relación de probabilidades compara las probabilidades de que el evento ocurra en 2 niveles diferentes del predictor. Minitab establece la comparación colocando los niveles en 2 columnas: nivel A y nivel B. El nivel B es el nivel de referencia para el factor. Las relaciones de probabilidades que son mayores que 1 indican que el evento es más probable en el nivel A. Las relaciones de probabilidades que son menores que 1 indican que el evento es menos probable en el nivel A. Para obtener información sobre codificación de predictores categóricos, vaya a Esquemas de codificación para predictores categóricos.
Relaciones de probabilidades para predictores categóricos
Nivel A Nivel B Relación de
probabilidadesIC de 95% Mes 2 1 1.1250 (0.0600, 21.0834) 3 1 3.3750 (0.2897, 39.3165) 4 1 7.7143 (0.7461, 79.7592) 5 1 2.2500 (0.1107, 45.7172) 6 1 6.0000 (0.5322, 67.6397) 3 2 3.0000 (0.2547, 35.3325) 4 2 6.8571 (0.6556, 71.7169) 5 2 2.0000 (0.0976, 41.0019) 6 2 5.3333 (0.4679, 60.7946) 4 3 2.2857 (0.4103, 12.7323) 5 3 0.6667 (0.0514, 8.6389) 6 3 1.7778 (0.2842, 11.1200) 5 4 0.2917 (0.0252, 3.3719) 6 4 0.7778 (0.1464, 4.1326) 6 5 2.6667 (0.2124, 33.4861) Resultado clave: Relación de probabilidades
En estos resultados, el predictor categórico es el mes desde el inicio de la temporada alta de un hotel. La respuesta es si un huésped cancela o no cancela una reservación. En este ejemplo, una cancelación es el evento. La mayor relación de probabilidades es aproximadamente 7,71, cuando el nivel A es el mes 4 y el nivel B es el mes 1. Esto indica que las probabilidades de que un huésped cancele una reservación en el mes 4 son aproximadamente 8 veces mayores que las probabilidades de que un huésped cancele una reservación en el mes 1.
Paso 4: Determinar hasta qué punto el modelo se ajusta a los datos
Para determinar qué tan bien se ajusta el modelo a los datos, examine los estadísticos de bondad de ajuste en la tabla Resumen del modelo.
Nota
Muchos de los estadísticos de resumen del modelo y de bondad de ajuste se ven afectados por cómo están ordenados los datos en la hoja de trabajo y si hay una prueba por fila o múltiples pruebas por fila. La prueba de Hosmer-Lemeshow no se ve afectada por cómo están ordenados los datos y es comparable entre una prueba por fila y múltiples pruebas por fila. Para obtener más información, vaya a Cómo los formatos de datos afectan la bondad de ajuste en regresión logística binaria.
- R-cuad. de desviación
-
Mientras más alto sea el valor de R2 de desviación, mejor se ajustará el modelo a los datos. El R2 de desviación siempre se encuentra entre 0% y 100%.
El R2 de desviación siempre se incrementa cuando usted agrega términos adicionales a un modelo. Por ejemplo, el mejor modelo de cinco términos siempre tendrá un R2 de desviación que será al menos tan alto como el mejor modelo de cuatro predictores. Por lo tanto, el R2 de desviación es más útil cuando se comparan modelos del mismo tamaño.
La organización de los datos afecta el valor de R2 de desviación. El R2 de desviación suele ser más alto para datos con múltiples pruebas por fila que para datos con una sola prueba por fila. Los valores de R2 de desviación son comparables solamente entre modelos que utilizan el mismo formato de datos.
Los estadísticos de bondad de ajuste son simplemente una medida de qué tan bien se ajusta el modelo a los datos. Incluso cuando un modelo tenga un valor deseable, usted deberá revisar las gráficas de residuos y las pruebas de bondad de ajuste para evaluar qué tan bien se ajusta un modelo a los datos.
- R-cuad. (ajust.) de desviación
-
Utilice el R2 de desviación ajustado para comparar modelos que tengan diferentes números de términos. El R2 de desviación siempre se incrementa cuando usted agrega un término al modelo. El valor ajustado de R2 de desviación incorpora el número de términos en el modelo como ayuda para elegir el modelo correcto.
- AIC, AICc y BIC
- Utilice el AIC, el AICc y el BIC para comparar diferentes modelos. Para cada estadístico, se prefieren valores más pequeños. Sin embargo, el modelo con el valor más pequeño para un conjunto de predictores no necesariamente ajusta los datos adecuadamente. Utilice también las pruebas de bondad de ajuste y las gráficas de residuos para evaluar hasta qué punto un modelo se ajusta a los datos.
Resumen del modelo
| R-cuadrado de la Desviación | R-cuadrado de la Desviación (ajust) | AIC | AICc | BIC |
|---|---|---|---|---|
| 95.81% | 95.16% | 243.85 | 245.80 | 255.32 |
Resultados clave: R-cuad. de desviación, R-cuad. (ajust) de desviación, AICc, BIC
En estos resultados, el modelo explica 95.81% de la desviación total en la variable de respuesta. Para estos datos, el valor de R2 de desviación indica que el modelo proporciona un ajuste adecuado a los datos. Si ajusta otros modelos con diferentes términos, utilice el valor de R2 de desviación ajustado, el valor de AIC, el valor de AICc y el valor de BIC para comparar qué tan bien se ajusta el modelo a los datos.
Paso 5: Determinar si el modelo no se ajusta a los datos
- Función de enlace incorrecta
- Término de orden superior omitido para las variables que están en el modelo
- Predictor omitido que no está en el modelo
- Dispersión excesiva
Si la desviación es estadísticamente significativa, usted puede probar con una función de enlace diferente o cambiar los términos incluidos en el modelo.
- Desviación: El valor p para la prueba de desviación tiende a ser menor para los datos que tienen un solo ensayo por organización de fila en comparación con los datos que poseen múltiples ensayos por fila, y, por lo general, disminuye a medida que disminuyen los ensayos por fila. Para los datos con un solo ensayo por fila, los resultados en formato Hosmer-Lemeshow son más confiables.
- Pearson: La aproximación a la distribución de chi-cuadrada que la prueba de Pearson utiliza resulta inexacta cuando el número de eventos esperados por fila en los datos es pequeño. De esta forma, la prueba de Pearson de bondad de ajuste resulta inexacta cuando los datos están en formato de un solo ensayo por fila.
- Hosmer-Lemeshow: La prueba de Hosmer-Lemeshow no depende del número de ensayos por fila en los datos como las otras pruebas de bondad de ajuste.Cuando los datos tienen pocos ensayos por fila, la prueba de Hosmer-Lemeshow es un indicador más fiable sobre qué tan bien se ajusta el modelo a los datos.
Pruebas de bondad de ajuste
| Prueba | GL | Chi-cuadrada | Valor p |
|---|---|---|---|
| Desviación | 44 | 32.26 | 0.905 |
| Pearson | 44 | 31.98 | 0.911 |
| Hosmer-Lemeshow | 7 | 4.18 | 0.758 |
Resultados clave para el formato de evento/ensayo: Información de respuesta, prueba de desviación, prueba de Pearson, prueba de Hosmer-Lemeshow
En estos resultados, todas las pruebas de bondad de ajuste tienen valores p mayores que el nivel de significancia habitual de 0,05. Las pruebas no proporcionan evidencia de que las probabilidades pronosticadas se desvíen de las probabilidades observadas de una manera que la distribución binomial no predice.
