En este tema
GL
El total de grados de libertad (GL) es la cantidad de información en los datos. El análisis utiliza esa información para estimar los valores de parámetros de población desconocidos. Este valor está determinado por el número de observaciones en la muestra. Los GL de un término muestran qué tanta información usa ese término. Si incrementa el tamaño de la muestra, obtendrá más información sobre la población, con lo cual aumenta el total de GL. Al aumentar el número de términos en el modelo, se utiliza más información, con lo cual se reducen los GL disponibles para estimar la variabilidad de las estimaciones de los parámetros.
- GL para curvatura
- Si un diseño tiene puntos centrales, entonces un GL es para la prueba de curvatura. Si el término para puntos centrales está en el modelo, la fila para curvatura es parte del modelo. Si el término para puntos centrales no está en el modelo, la fila para curvatura es parte del error que se utiliza para probar los términos que están en el modelo.
- GL para error
- Si se cumplen dos condiciones, entonces Minitab particiona los GL para error que no son para curvatura. La primera condición es que debe haber términos que se pueden ajustar con los datos que no están en el modelo actual. Por ejemplo, si su diseño tiene bloques, pero los bloques no están en el modelo. El término de punto central es siempre para curvatura, por lo que el término de punto central no cuenta como un término que usted pueda ajustar con los datos que no están en el modelo actual.
SC ajust.
Las sumas ajustadas de los cuadrados son medidas de variación para los diferentes componentes del modelo. El orden de los predictores en el modelo no afecta el cálculo de las sumas ajustadas de los cuadrados. En la tabla Análisis de varianza, Minitab separa las sumas de los cuadrados en diferentes componentes que describen la variación que se debe a fuentes diferentes.
- SC ajust. para el modelo
- La suma ajustada de los cuadrados para el modelo es la diferencia entre la suma total de los cuadrados y la suma de los cuadrados del error del modelo en comparación con un modelo que solo utilice la media de la respuesta. Es la suma de todas las sumas secuenciales de los cuadrados para los términos incluidos en el modelo.
- SC ajust. para grupos de términos
- La suma ajustada de los cuadrados para un grupo de términos incluidos en el modelo es la suma de las sumas secuenciales de los cuadrados para todos los términos del grupo. Cuantifica la cantidad de variación en los datos de respuesta que es explicada por el grupo de términos.
- SC ajust. para un término
- La suma ajustada de los cuadrados de un término es el aumento en la suma de los cuadrados del modelo en comparación de un modelo que solo tenga los otros términos. Cuantifica la cantidad de variación en los datos de respuesta que explicada por cada término incluido en el modelo.
- SC ajust. para el error
- La suma ajustada de los cuadrados para el error es la suma de los residuos cuadráticos. Cuantifica la variación en los datos que los predictores no explican.
- SC ajust. para curvatura
- La suma ajustada de los cuadrados para curvatura puede ser parte de la suma de los cuadrados del modelo o parte de la suma de los cuadrados del error. Cuantifica la cantidad de variación en los datos de respuesta que es explicada por el término de punto central. Esta variación representa el efecto combinado de uno o más términos cuadráticos.
- SC ajust. para el error puro
- La suma ajustada de los cuadrados del error puro es parte de la suma de los cuadrados del error. La suma de los cuadrados del error puro existe cuando existen los grados de libertad para el error puro. Para obtener más información, vaya a la sección sobre Grados de libertad (GL). Cuantifica la variación en los datos para observaciones con los mismos valores de los factores, bloques y covariables.
- SC ajust. total
- La suma total ajustada de los cuadrados es la suma de la suma de los cuadrados del modelo y la suma de los cuadrados del error. Cuantifica la variación total en los datos.
Interpretación
Minitab utiliza las sumas ajustadas de los cuadrados para calcular los valores p en la tabla ANOVA. Minitab también utiliza las sumas de los cuadrados para calcular el estadístico de R2. Por lo general, se interpretan los valores p y el estadístico R2 ajustado en lugar de las sumas de los cuadrados.
CM Ajust.
Los cuadrados medios ajustados miden qué tanta variación explica un término o un modelo, asumiendo que todos los demás términos están en el modelo, independientemente de su orden en el modelo. A diferencia de las sumas ajustadas de los cuadrados, los cuadrados medios ajustados consideran los grados de libertad.
El cuadrado medio ajustado del error (también llamado MSE o s2) es la varianza alrededor de los valores ajustados.
Interpretación
Minitab utiliza los cuadrados medios ajustados para calcular los valores p en la tabla ANOVA. Minitab también utiliza los cuadrados medios ajustados para calcular el estadístico de R2 ajustado. Generalmente, se interpretan los valores p y el estadístico de R2 ajustado en lugar de los cuadrados medios ajustados.
SC sec.
Las sumas secuenciales de los cuadrados son medidas de variación para diferentes componentes del modelo. A diferencia de las sumas ajustadas de los cuadrados, las sumas secuenciales de los cuadrados dependen del orden en el que los términos están en el modelo. En la tabla Análisis de varianza, Minitab separa las sumas secuenciales de los cuadrados en diferentes componentes que describen la variación que se debe a diferentes fuentes.
- SC sec. para el modelo
- La suma secuencial de los cuadrados para el modelo es la diferencia entre la suma total de los cuadrados y la suma de los cuadrados del error. Es la suma de todas las sumas de los cuadrados para los términos incluidos en el modelo.
- SC sec. para grupos de términos
- La suma secuencial de los cuadrados para un grupo de términos incluidos en el modelo es la suma de las sumas de los cuadrados para todos los términos del grupo. Cuantifica la cantidad de variación en los datos de respuesta que es explicada por el grupo de términos.
- SC sec. para un término
- La suma secuencial de los cuadrados para un término es el aumento en la suma de los cuadrados del modelo en comparación con un modelo que solo contenga los términos que aparecen por encima de este en la tabla ANOVA. Cuantifica el aumento en la suma de los cuadrados del modelo cuando ese término se agrega a un modelo con los términos que aparecen por encima de este.
- SC sec. para el error
- La suma secuencial de los cuadrados del error es la suma de los residuos cuadráticos. Cuantifica la variación en los datos que los predictores no explican.
- SC sec. para curvatura
- La suma secuencial de los cuadrados para curvatura puede ser parte de la suma de los cuadrados del modelo o parte de la suma de los cuadrados del error. Cuantifica la cantidad de variación en los datos de respuesta que es explicada por el término de punto central. Esta variación representa el efecto combinado de uno o más términos cuadráticos.
- SC sec. para el error puro
- La suma secuencial de los cuadrados del error puro es parte de la suma de los cuadrados del error. La suma de los cuadrados del error puro existe cuando existen los grados de libertad para el error puro. Para obtener más información, vaya a la sección sobre Grados de libertad (GL). Cuantifica la variación en los datos para observaciones con los mismos valores de los factores, bloques y covariables.
- SC sec. total
- La suma secuencial total de los cuadrados es la suma de la suma de los cuadrados del modelo y la suma de los cuadrados del error. Cuantifica la variación total en los datos.
Interpretación
Minitab no utiliza la suma secuencial de los cuadrados para calcular los valores p cuando usted analiza un diseño, pero puede usar la suma secuencial de los cuadrados cuando usted utiliza Ajustar modelo de regresión o Ajustar modelo lineal general. Por lo general, los valores p y el estadístico R2 se interpretan con base en las sumas ajustadas de los cuadrados.
Contribución
La contribución muestra el porcentaje con el que cada fuente en la tabla Análisis de varianza contribuye a las sumas de cuadrados secuenciales totales (SC Sec.).
Interpretación
Porcentajes mayores indican que la fuente representa más de la variación en la respuesta.
Valor F
Un valor F aparece para cada prueba en la tabla Análisis de varianza.
- Valor F para el modelo
- El valor F es el estadístico de prueba que se utiliza para determinar si cualquier término incluido en el modelo está asociado con la respuesta, incluyendo covariables, bloques, términos de factores y curvatura.
- Valor F para covariables como un grupo
- El valor F es el estadístico de prueba utilizado para determinar si cualquiera de las covariables está asociada con la respuesta simultáneamente.
- Valor F para covariables individuales
- El valor F es el estadístico de prueba utilizado para determinar si una covariable individual está asociada con la respuesta.
- Valor F para bloques
- El valor F es el estadístico de prueba utilizado para determinar si condiciones diferentes entre los bloques están asociadas con la respuesta.
- Valor F para tipos de términos de factores
- El valor F es el estadístico de prueba utilizado para determinar si un grupo de términos está asociado con la respuesta. Algunos ejemplos de grupos de términos son los efectos lineales y las interacciones de 2 factores.
- Valor F para términos individuales
- El valor F es el estadístico de prueba utilizado para determinar si el término está asociado con la respuesta.
- Valor F para curvatura
- El valor F es el estadístico de prueba utilizado para determinar si cualquiera de los factores tiene una relación curva con la respuesta.
- Valor F para la prueba de falta de ajuste
- El valor F es el estadístico de prueba utilizado para determinar si faltan términos en el modelo que incluyen los factores especificados en el experimento. Si se eliminan bloques o covariables del modelo mediante un procedimiento escalonado, entonces la prueba de falta de ajuste también incluye estos términos.
Interpretación
Minitab utiliza el valor F para calcular el valor p, que se usa para tomar una decisión acerca de la significancia estadística de la prueba. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula. Un valor F lo suficientemente grande indica significancia estadística.
Si desea usar el valor F para determinar si puede rechazar la hipótesis nula, compare el valor F con su valor crítico. Puede calcular el valor crítico en Minitab o buscar el valor crítico en una tabla de la distribución F en la mayoría de los libros de estadística. Para obtener más información sobre cómo usar Minitab para calcular el valor crítico, vaya a Uso de la función de distribución acumulada inversa (ICDF) y haga clic en "Usar la ICDF para calcular los valores críticos".
Valor p – Modelo
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Para determinar si el modelo explica la variación en la respuesta, compare el valor p del modelo con el nivel de significancia para evaluar la hipótesis nula. La hipótesis nula del modelo es que el modelo no explica ninguna variación en la respuesta. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que el modelo explica la variación en la respuesta cuando no es así.
- Valor p ≤ α: El modelo explica la variación en la respuesta
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que el modelo explica la variación en la respuesta.
- Valor p > α: No hay suficiente evidencia para concluir que el modelo explica la variación en la respuesta
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que el modelo explica la variación en la respuesta. Convendría que ajuste un nuevo modelo.
Valor p – Covariables
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
En un experimento diseñado, las covariables representan variables que son medibles, pero difíciles de controlar. Por ejemplo, miembros de un equipo de control de calidad en una red de hospitales diseñan un experimento para estudiar la duración de la estadía de pacientes admitidos para cirugía de reemplazo total de rodilla. Para el experimento, el equipo puede controlar factores como el formato de las instrucciones antes de la operación. Para evitar sesgos, el equipo registra datos sobre covariables que no pueden controlar, como la edad del paciente.
Interpretación
Para determinar si la asociación entre la respuesta y una covariable es estadísticamente significativa, compare el valor p de la covariable con el nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que el coeficiente de la covariable es cero, lo que implica que no hay asociación entre la covariable y la respuesta.
Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que condiciones diferentes en la ejecución de las corridas producen un cambio en la respuesta cuando en realidad no es así.
Cuando usted evalúa la significancia estadística de los términos de un modelo con covariables, considere los factores de inflación de la varianza (FIV).
- Valor p ≤ α: La asociación es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que la asociación entre la respuesta y la covariable es estadísticamente significativa.
- Valor p > α: La asociación no es estadísticamente significativa
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que la asociación entre la respuesta y la covariable es estadísticamente significativa. Le convendría ajustar un modelo sin la covariable.
Nota
Todos los valores de FIV son 1 en la mayoría de los diseños factoriales, lo que simplifica la determinación de significancia estadística. La inclusión de covariables en el modelo y la ocurrencia de corridas divergentes durante la recolección de datos son dos formas comunes de aumentar los valores de FIV, lo cual complica la interpretación de significancia estadística. Los valores de FIV están en la tabla Coeficientes. Para obtener más información, vaya a Tabla Coeficientes para Analizar diseño factorial y haga clic en FIV.
Valor p – Bloques
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Los bloques representan las diferencias que puede ocurrir entre corridas que se realizan en diferentes condiciones. Por ejemplo, un ingeniero diseña un experimento para estudiar soldaduras y no puede recolectar todos los datos el mismo día. La calidad de la soldadura se ve afectada por varias variables que cambian día a día que el ingeniero no puede controlar, tales como la humedad relativa. Para tomar en consideración estas variables no controlables, el ingeniero agrupa las corridas realizadas cada día en bloques separados. Los bloques representan la variación de las variables no controlables, de manera que estos efectos no se confundan con los efectos de los factores que el ingeniero desea estudiar. Para obtener más información sobre cómo Minitab asigna las corridas a los bloques, vaya a ¿Qué es un bloque?.
Interpretación
Para determinar si diferentes condiciones entre corridas cambian la respuesta, compare el valor p de los bloques con su nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que diferentes condiciones no cambian la respuesta.
Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que condiciones diferentes en la ejecución de las corridas producen un cambio en la respuesta cuando en realidad no es así.
- Valor p ≤ α: Diferentes condiciones cambian la respuesta
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que diferentes condiciones cambian la respuesta.
- Valor p > α: No hay suficiente evidencia para concluir que diferentes condiciones cambian la respuesta
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que diferentes condiciones cambian la respuesta. Le convendría ajustar un modelo sin bloques.
Valor p – Factores, interacciones y grupos de términos
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
- Si una covariable es significativa, usted puede concluir que el coeficiente de la covariable no es igual a cero.
- Si un factor categórico es significativo, usted puede concluir que no todas las medias de nivel son iguales.
- Si un término de interacción es significativo, usted puede concluir que la relación entre un factor y la respuesta depende del resto de los factores en el término.
Pruebas de grupos de términos
Si un grupo de términos es estadísticamente significativo, entonces usted puede concluir que por lo menos uno de los términos en el grupo tiene un efecto en la respuesta. Cuando utiliza significancia estadística para decidir cuáles términos mantener en un modelo, generalmente no elimina grupos completos de términos al mismo tiempo. La significancia estadística de términos individuales puede cambiar debido a los términos en el modelo.
Análisis de Varianza
| Fuente | GL | SC Ajust. | MC Ajust. | Valor F | Valor p |
|---|---|---|---|---|---|
| Modelo | 10 | 447.766 | 44.777 | 17.61 | 0.003 |
| Lineal | 4 | 428.937 | 107.234 | 42.18 | 0.000 |
| Material | 1 | 181.151 | 181.151 | 71.25 | 0.000 |
| PresIny | 1 | 112.648 | 112.648 | 44.31 | 0.001 |
| TempIny | 1 | 73.725 | 73.725 | 29.00 | 0.003 |
| TempEnfr | 1 | 61.412 | 61.412 | 24.15 | 0.004 |
| Interacciones de 2 términos | 6 | 18.828 | 3.138 | 1.23 | 0.418 |
| Material*PresIny | 1 | 0.342 | 0.342 | 0.13 | 0.729 |
| Material*TempIny | 1 | 0.778 | 0.778 | 0.31 | 0.604 |
| Material*TempEnfr | 1 | 4.565 | 4.565 | 1.80 | 0.238 |
| PresIny*TempIny | 1 | 0.002 | 0.002 | 0.00 | 0.978 |
| PresIny*TempEnfr | 1 | 0.039 | 0.039 | 0.02 | 0.906 |
| TempIny*TempEnfr | 1 | 13.101 | 13.101 | 5.15 | 0.072 |
| Error | 5 | 12.712 | 2.542 | ||
| Total | 15 | 460.478 |
En este modelo, la prueba para las interacciones de dos factores no es estadísticamente significativa en el nivel 0.05. Además, las pruebas para todas las interacciones de 2 factores no son estadísticamente significativas.
Análisis de Varianza
| Fuente | GL | SC Ajust. | MC Ajust. | Valor F | Valor p |
|---|---|---|---|---|---|
| Modelo | 5 | 442.04 | 88.408 | 47.95 | 0.000 |
| Lineal | 4 | 428.94 | 107.234 | 58.16 | 0.000 |
| Material | 1 | 181.15 | 181.151 | 98.24 | 0.000 |
| PresIny | 1 | 112.65 | 112.648 | 61.09 | 0.000 |
| TempIny | 1 | 73.73 | 73.725 | 39.98 | 0.000 |
| TempEnfr | 1 | 61.41 | 61.412 | 33.31 | 0.000 |
| Interacciones de 2 términos | 1 | 13.10 | 13.101 | 7.11 | 0.024 |
| TempIny*TempEnfr | 1 | 13.10 | 13.101 | 7.11 | 0.024 |
| Error | 10 | 18.44 | 1.844 | ||
| Total | 15 | 460.48 |
Si usted reduce el modelo un término por vez, comenzando con la interacción de 2 factores con el valor p más alto, entonces la última interacción de 2 factores es estadísticamente significativa en el nivel de 0.05.
Valor p – Curvatura
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Minitab evalúa la curvatura cuando el diseño tiene puntos centrales. La prueba observa la media ajustada de la respuesta en los puntos centrales con relación a la media esperada si las relaciones entre los términos del modelo y la media son lineales. Para visualizar la curvatura, utilice gráficas factoriales.
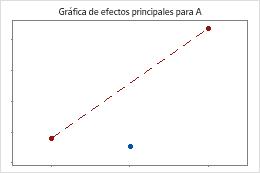
Los puntos centrales están alejados de la línea que une las medias de los puntos de vértice, lo cual sugiere una relación curva. Utilice el valor p para verificar que la curvatura es estadísticamente significativa.
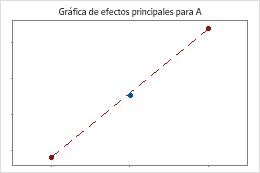
Los puntos centrales están cerca de la línea que une las medias de los puntos de vértice. La curvatura probablemente no sea estadísticamente significativa.
Interpretación
Para determinar si por lo menos uno de los factores tiene una relación curva con la respuesta, compare el valor p de la curvatura con su nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que todas las relaciones entre los factores y la respuesta son lineales.
Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que condiciones diferentes en la ejecución de las corridas producen un cambio en la respuesta cuando en realidad no es así.
- Valor p ≤ α: Por lo menos un factor tiene una relación curva con la respuesta
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que por lo menos uno de los factores tiene una relación curva con la respuesta. Se recomienda agregar puntos axiales al diseño, de forma que usted pueda modelar la curvatura.
- Valor p > α: No hay suficiente evidencia para concluir que algún factor tiene una relación curva con la respuesta
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que alguno de los factores tiene una relación curva con la respuesta. Si la curvatura es parte del modelo, se recomienda que vuelva a ajustar el modelo sin un término para puntos centrales, de forma que la curvatura sea parte del error.
Nota
Generalmente, si la curvatura no es estadísticamente significativa, usted elimina el término de punto central. Si deja los puntos centrales en el modelo, Minitab presupone que el modelo contiene curvatura que el diseño factorial no puede ajustar. Debido al ajuste inadecuado, Gráfica de contorno, Gráfica de superficie y Gráfica superpuesta de contornos no están disponibles. Además, Minitab no hace una interpolación entre los niveles de factores en el diseño con el Optimizador de respuestas. Para obtener más información sobre formas de utilizar el modelo, vaya a Revisión general del modelo almacenado.
Valor p – Falta de ajuste
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
- Valor p ≤ α: La falta de ajuste es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que el modelo no especifica correctamente la relación. Para mejorar el modelo, es posible que tenga que agregar términos o transformar los datos.
- Valor p > α: La falta de ajuste no es estadísticamente significativa
-
Si el valor p es mayor que el nivel de significancia, la prueba no detecta ninguna falta de ajuste.
