En este tema
GL
El total de grados de libertad (GL) es la cantidad de información en los datos. El análisis utiliza esa información para estimar los valores de los coeficientes. El total de GL es 1 menos que el número de filas en los datos. Los GL de un término muestran cuántos coeficientes usa ese término. Aumentar el número de términos en el modelo agrega más coeficientes al modelo, lo que reduce los GL para el error. Los GL para el error son los grados de libertad restantes que no se usan en el modelo.
Nota
Para un diseño factorial de 2 niveles o un diseño de Plackett-Burman, si un diseño tiene puntos centrales, entonces un GL es para la prueba de curvatura. Si el término para puntos centrales está en el modelo, la fila para curvatura es parte del modelo. Si el término para puntos centrales no está en el modelo, la fila para curvatura es parte del error que se utiliza para probar los términos que están en el modelo. En los diseños de superficie de respuesta y de cribado definitivo, usted puede estimar los términos cuadráticos, por lo que la prueba de curvatura no es necesaria.
Desv. sec.
- Modelo
- La desviación secuencial para el modelo de regresión cuantifica qué cantidad de la desviación total explica el modelo.
- Término
- La desviación secuencial para un término cuantifica la diferencia entre un modelo hasta e incluyendo un término particular, con el término y sin el término.
- Error
- La desviación secuencial para el error cuantifica la desviación que el modelo no explica.
- Total
- La desviación secuencial total es la suma de la desviación secuencial para el modelo y la desviación secuencial para el error. La desviación secuencial total cuantifica la desviación total en los datos.
Interpretación
Cuando usted especifica el uso de la desviación secuencial para las pruebas, Minitab utiliza la desviación secuencial para calcular los valores p para el modelo de regresión y los términos individuales. Por lo general, usted interpreta los valores p en lugar de la desviaicón secuencial.
Contribución
La contribución muestra el porcentaje que cada fuente incluida en la tabla ANOVA aporta a la desviación secuencial total.
Interpretación
Los porcentajes más altos indican que la fuente representa una mayor parte de la desviación en la variable de respuesta. La contribución porcentual para el modelo de regresión es igual al R2 de desviación.
Desv. ajust.
Las desviaciones ajustadas son medidas de la variación para los diferentes componentes del modelo. El orden de los predictores en el modelo no afecta el cálculo de las desviaciones ajustadas. En la tabla Desviación, Minitab separa la desviación en diferentes componentes que describen la desviación que explican las diferentes fuentes.
- Modelo
- La desviación ajustada para el modelo de regresión cuantifica la diferencia entre el modelo actual y el modelo de las constantes.
- Término
- La desviación ajustada para un término cuantifica la diferencia entre un modelo con el término y sin el término.
- Error
- La desviación ajustada para el error cuantifica la desviación que el modelo no explica.
- Total
- La desviación ajustada total es la suma de la desviación ajustada para el modelo y la desviación ajustada para el error. La desviación ajustada total cuantifica la desviación total en los datos.
Interpretación
Minitab utiliza las desviaciones ajustadas para calcular el valor p de un término. Minitab también utiliza las desviaciones ajustadas para calcular el estadístico R2 de desviación. Por lo general, usted interpreta los valores p y el estadístico R2 en lugar de las desviaciones.
Media ajust.
La desviación media ajustada mide la cantidad de desviación que un término o modelo explica por cada grado de libertad. El cálculo de la desviación media ajustada para cada término presupone que todos los demás términos están en el modelo.
Interpretación
Minitab utiliza el valor de chi-cuadrada para calcular el valor p de un término. Por lo general, usted interpreta los valores p en lugar de los mínimos cuadrados ajustados.
Chi-cuadrada
Cada término de la tabla ANOVA tiene un valor de chi-cuadrada. El valor de chi-cuadrada es el estadístico de prueba que determina si un término o modelo tiene asociación con la respuesta.
Interpretación
Minitab utiliza el estadístico de chi-cuadrada para calcular el valor p, que se usa para tomar una decisión acerca de la significancia estadística de los términos y el modelo. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula. Un estadístico de chi-cuadrada lo suficientemente grande da como resultado un valor p pequeño, lo que indica que el término o el modelo es estadísticamente significativo.
Valor p – Modelo
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
- Valor p ≤ α: Por lo menos un coeficiente es diferente de 0
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que por lo menos un coeficiente es diferente de 0.
- Valor p > α: No existe suficiente evidencia para concluir que por lo menos un coeficiente es diferente de 0.
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que por lo menos un coeficiente es diferente de 0. Convendría que ajuste un nuevo modelo.
Las pruebas en la tabla Desviación son pruebas de relación de probabilidad. La prueba en la muestra expandida de la tabla Coeficientes son pruebas de aproximación de Wald. Las pruebas de relación de probabilidad son más exactas para las muestras pequeñas que las pruebas de aproximación de Wald.
Valor p – Término
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
- Valor p ≤ α: La asociación es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que hay una asociación estadísticamente significativa entre la variable de respuesta y el término.
- Valor p > α: La asociación no es estadísticamente significativa
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que existe una asociación estadísticamente significativa entre la variable de respuesta y el término. Le convendría reajustar el modelo sin el término.
- Si un factor continuo es significativo, usted puede concluir que el coeficiente del factor es diferente de cero.
- Si un factor categórico es significativo, usted puede concluir que la probabilidad del evento no es la misma para todos los niveles del factor.
- Si un término de interacción es significativo, usted puede concluir que la relación entre un factor y la probabilidad del evento depende del resto de los factores en el término.
- Si un término cuadrático es significativo, usted puede concluir que la superficie de respuesta presenta una curvatura.
Las pruebas incluidas en la tabla Análisis de varianza son pruebas de relación de verosimilitud. La prueba en la muestra expandida de la tabla Coeficientes son pruebas de aproximación de Wald. Las pruebas de relación de probabilidad son más exactas para las muestras pequeñas que las pruebas de aproximación de Wald.
Valor p – Curvatura
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Minitab evalúa la curvatura cuando el diseño tiene puntos centrales. La prueba observa la media ajustada de la respuesta en los puntos centrales con relación a la media esperada si las relaciones entre los términos del modelo y la media son lineales. Para visualizar la curvatura, utilice gráficas factoriales.
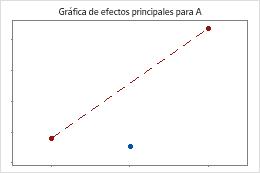
Los puntos centrales están alejados de la línea que une las medias de los puntos de vértice, lo cual sugiere una relación curva. Utilice el valor p para verificar que la curvatura es estadísticamente significativa.
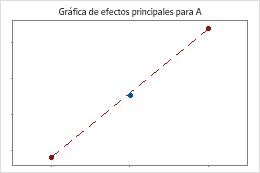
Los puntos centrales están cerca de la línea que une las medias de los puntos de vértice. La curvatura probablemente no sea estadísticamente significativa.
Interpretación
Para determinar si por lo menos uno de los factores tiene una relación curva con la respuesta, compare el valor p de la curvatura con su nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que todas las relaciones entre los factores y la respuesta son lineales.
Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que condiciones diferentes en la ejecución de las corridas producen un cambio en la respuesta cuando en realidad no es así.
- Valor p ≤ α: Por lo menos un factor tiene una relación curva con la respuesta
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que por lo menos uno de los factores tiene una relación curva con la respuesta. Se recomienda agregar puntos axiales al diseño, de forma que usted pueda modelar la curvatura.
- Valor p > α: No hay suficiente evidencia para concluir que algún factor tiene una relación curva con la respuesta
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que alguno de los factores tiene una relación curva con la respuesta. Si la curvatura es parte del modelo, se recomienda que vuelva a ajustar el modelo sin un término para puntos centrales, de forma que la curvatura sea parte del error.
Nota
Generalmente, si la curvatura no es estadísticamente significativa, usted elimina el término de punto central. Si deja los puntos centrales en el modelo, Minitab presupone que el modelo contiene curvatura que el diseño factorial no puede ajustar. Debido al ajuste inadecuado, Gráfica de contorno, Gráfica de superficie y Gráfica superpuesta de contornos no están disponibles. Además, Minitab no hace una interpolación entre los niveles de factores en el diseño con el Optimizador de respuestas. Para obtener más información sobre formas de utilizar el modelo, vaya a Revisión general del modelo almacenado.
