En este tema
Prueba de comparaciones múltiples
Intervalos de comparaciones múltiples para muestras k > 2
Sea 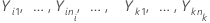 supongamos que k > 2 son muestras independientes, donde cada muestra es independiente y está distribuida idénticamente con la media
supongamos que k > 2 son muestras independientes, donde cada muestra es independiente y está distribuida idénticamente con la media 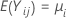 y varianza
y varianza  . Y supongamos que las muestras provienen de poblaciones que tienen una curtosis común.
. Y supongamos que las muestras provienen de poblaciones que tienen una curtosis común. 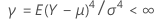
Y sea 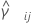 sea un estimador de curtosis agrupada para el par de muestras ( i, j) determinado como:
sea un estimador de curtosis agrupada para el par de muestras ( i, j) determinado como:
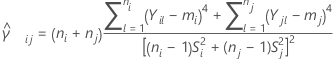
Sea 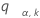 sea el superior un punto del rango de las variables k que son independientes y distribuidas idénticamente en una distribución aleatoria normal estándar. Es decir,
sea el superior un punto del rango de las variables k que son independientes y distribuidas idénticamente en una distribución aleatoria normal estándar. Es decir, 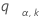 satisface lo siguiente:
satisface lo siguiente:
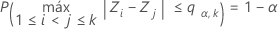
donde Z1, ..., Zk son variables aleatorias normales estándar independientes y distribuidas idénticamente. Barnard (1978) proporciona un algoritmo numérico simple basado en una cuadratura gaussiana de 16 puntos para calcular la función de distribución del rango normal.
El procedimiento de comparaciones múltiples rechaza la hipótesis nula de igualdad de varianzas (también denominada homogeneidad de varianzas) si, y únicamente si, al menos un par de los intervalos siguientes no se sobrepone:
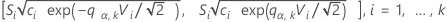
donde
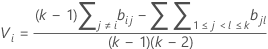
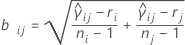
donde ri = (ni - 3) / ni.
Nos referimos a los intervalos arriba mencionados como intervalos de comparaciones múltiples o Intervalos de CM. Los intervalos de CM de cada muestra no se deben interpretar como intervalos de confianza para las desviaciones estándar de las poblaciones parentales. Hochberg et al. (1982) hacen referencia a intervalos similares para comparar medias como "intervalos de incertidumbre". Los intervalos de CM dados aquí solo son útiles para comparar las desviaciones estándar o varianzas de los diseños de múltiples muestras. Cuando la prueba general de comparaciones múltiples es significativa, las desviaciones estándar que corresponden a los intervalos que no se solapan son estadísticamente diferentes. (Para la derivación detallada de estos intervalos, vaya al artículo técnico sobre Métodos de comparaciones múltiples.)
Intervalos de comparaciones múltiples para muestras k = 2
Donde hay únicamente dos muestras, los intervalos de comparaciones múltiples son determinados por:

donde zα / 2 es el punto percentil α / 2 superior de la distribución normal estándar, ci = ni / ni - zα / 2 y Vi es determinado por la siguiente fórmula:
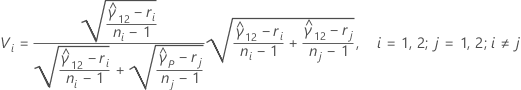
Valor p para la prueba
Si hay 2 muestras en el diseño, entonces Minitab calcula el valor p para la prueba de comparaciones múltiples utilizando el método de Bonett para una prueba de 2 varianzas y una relación hipotética, Po, de 1.
Si hay muestras k > 2 en el diseño, entonces sea Pi j siendo el valor p de la prueba para cualquier par (i, j ) de muestras. El valor p del procedimiento de comparaciones múltiples como una prueba general de igualdad de varianzas es determinado por lo siguiente:

Para obtener más información, incluyendo las simulaciones y los algoritmos detallados para calcular Pi j , consulte el Método de Bonett, que es un artículo técnico que tiene simulaciones y otras informaciones sobre el Método de Bonett.
Notación
| Término | Description |
|---|---|
| ni | el número de observaciones en la muestra i |
| Y i l | la Iésima observación en la muestra i |
| mi | la media recortada de la muestra i con proporciones de recorte de  |
| k | el número de muestras |
| Si | la desviación estándar de la muestra i |
| α | el nivel de significancia para la prueba = 1 - (el nivel de confianza / 100) |
| Ci | 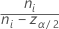 |
| Zα / 2 | el punto percentil α / 2 superior de la distribución normal estándar |
| ri |  |
Estadístico de prueba de Levene
Minitab muestra un estadístico de prueba y un valor p para la prueba de Levene. La hipótesis nula es que las varianzas son iguales y la hipótesis alternativa es que las varianzas no son iguales. Utilice la prueba de Levene cuando los datos provengan de distribuciones continuas, pero no necesariamente distribuciones normales.
El método de cálculo de la prueba de Levene es una modificación del procedimiento de Levene (Levene, 1960) desarrollado por Brown y Forsythe (1974). Este método considera las distancias de las observaciones con respecto a la mediana de la muestra en lugar de la media de la muestra. Al usar la mediana de la muestra en vez de la media de la muestra, esto hace que la prueba sea más sólida para las muestras más pequeñas y hace el procedimiento asintóticamente libre de distribución. Si el valor p es menor que el nivel ɑ, se rechaza la hipótesis nula de que las varianzas son iguales.
Fórmula

- H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
- M. B. Brown y A. B. Forsythe (1974). “Robust tests for the equality of variance," Journal of the American Statistical Association, 69, 364-367.
Notación
| Término | Description |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
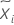 | mediana |
Estadístico de prueba de Bartlett
Minitab muestra un estadístico de prueba y un valor p para la prueba de Bartlett. Cuando únicamente hay dos niveles, Minitab realiza una prueba F en lugar de la prueba de Bartlett. Para estas pruebas, la hipótesis nula es que las varianzas son iguales y la hipótesis alternativa es que las varianzas no son iguales. Utilice la prueba de Bartlett cuando los datos provengan de distribuciones normales; la prueba de Bartlett no es sólida cuando los datos se apartan de la normalidad.
El estadístico de prueba de Bartlett calcula el promedio aritmético ponderado y el promedio geométrico ponderado de cada varianza de muestra basada en los grados de libertad. Mientras mayor sea la diferencia en los promedios, es más probable que las varianzas de las muestras no sean iguales. B sigue una distribución χ2 con k – 1 grados de libertad. Si el valor p es menor que el nivel ɑ, se rechaza la hipótesis nula de que las varianzas son iguales.
Fórmula
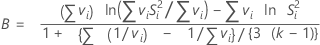
Notación
| Término | Description |
|---|---|
| si2 |  |
| k | número de muestras |
| vi | ni - 1 |
| ni | número de observaciones al iésimo nivel del factor |
Estadístico de prueba F
Cuando únicamente hay dos niveles, Minitab realiza una prueba F en lugar de la prueba de Bartlett. La hipótesis nula es que las varianzas son iguales y la hipótesis alternativa es que las varianzas no son iguales. Utilice el estadístico F cuando los datos provengan de distribuciones normales.
Si el valor p es menor que el nivel ɑ, se rechaza la hipótesis nula de que las varianzas son iguales.
Fórmula
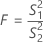
Fórmula para el valor p
- Para una prueba unilateral con una hipótesis alternativa del tipo "menor que", el valor p es igual a la probabilidad de obtener un estadístico F que sea igual a o menor que el valor observado a partir de una distribución F con grados de libertad GL1 y GL2.
- Para una prueba bilateral donde la relación es menor que 1, el valor p es igual a dos veces el área por debajo de la curva F menor que el valor observado a partir de una distribución F con grados de libertad GL1 y GL2.
- Para una prueba bilateral donde la relación es mayor que 1, el valor p es igual a dos veces el área por debajo de la curva F mayor que el valor observado a partir de una distribución F con grados de libertad GL1 y GL2.
- Para una prueba unilateral con una hipótesis alternativa del tipo "mayor que", el valor p es igual a la probabilidad de obtener un estadístico F que sea igual a o mayor que el valor observado a partir de una distribución F con grados de libertad GL1 y GL2.
Notación
| Término | Description |
|---|---|
| S12 | varianza de la muestra 1 |
| S22 | varianza de la muestra 2 |
| n1 - 1 | grados de libertad para el numerador |
| n2 - 1 | grados de libertad para el denominador |
Desviación estándar (Desv.Est.)
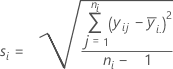
Notación
| Término | Description |
|---|---|
| yij | observaciones al i ésimo nivel del factor |
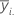 | media de observaciones al i ésimo nivel factor del factor |
| ni | número de observaciones al i ésimo nivel del factor |
Intervalos de confianza de Bonferroni
Minitab calcula los intervalos de confianza para las desviaciones estándar utilizando el método de Bonferroni. Un intervalo de confianza es un rango de valores que probablemente incluya algunos parámetros de población, en este caso, contiene la desviación estándar.
Los intervalos de confianza estándar se calculan utilizando un nivel de confianza 1 – α / 2. El método de Bonferroni utiliza el nivel de confianza 1 – α / 2p para cada intervalo de confianza individual, donde p es el número de factor y las combinaciones de nivel. El método garantiza que el conjunto de intervalos de confianza tengan un nivel de confianza de al menos 1 – α. El método de Bonferroni proporciona intervalos de confianza (más amplios) más conservadores, lo que reduce la probabilidad de error de tipo 1.
