En este tema
Gráfica de probabilidad
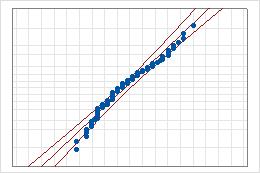
- Línea intermedia
- El percentil esperado de la distribución con base en estimaciones del parámetro de probabilidad máxima.
- Líneas de bordes de confianza
- Una línea izquierda curva indica los bordes inferiores de los intervalos de confianza para los percentiles. Una línea derecha curva indica los bordes superiores de los intervalos de confianza para los percentiles.
Interpretación
Utilice la gráfica de probabilidad para evaluar en qué grado sus datos siguen cada distribución.
Si la distribución provee un ajuste adecuado para los datos, los puntos deben ubicarse cerca de la línea de distribución ajustada, a lo largo de la misma. Alejamientos de la línea recta indican que el ajuste es inaceptable.
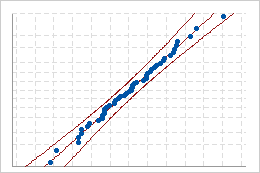
Ajuste adecuado
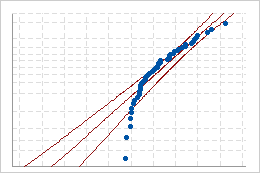
Ajuste deficiente
Además de la gráfica de probabilidad, utilice las medidas de bondad de ajuste, tales como los valores p para AD y los valores p para LRT, para evaluar el ajuste de distribución.
- Elija la distribución que se utiliza más frecuentemente en su industria o aplicación.
- Elija la distribución que proporciona los resultados más conservadores. Por ejemplo, si usted realiza un análisis de capacidad, puede realizar el análisis utilizando diferentes distribuciones y luego elegir la distribución que produzca los índices de capacidad más conservadores. Para obtener más información, vaya a Percentiles de distribución para Identificación de distribución individual y haga clic en "Porcentajes y percentiles".
- Elija la distribución más simple que se ajuste adecuadamente a sus datos. Por ejemplo, si tanto una distribución de 2 parámetros como otra de 3 parámetros proporcionan un buen ajuste, usted podría elegir la distribución más simple de 2 parámetros.
AD
El estadístico de bondad de ajuste de Anderson-Darling (AD) es una medida de las desviaciones entre la línea ajustada (con base en la distribución seleccionada) y la función de paso no paramétrica (con base en los puntos de datos). El estadístico de Anderson-Darling es una distancia elevada al cuadrado que tiene mayor ponderación en las colas de la distribución.
Interpretación
Minitab utiliza el estadístico de Anderson-Darling para calcular el valor p. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula de que los datos siguen la distribución.
Generalmente, valores substancialmente menores del estadístico de Anderson-Darling indican que los datos siguen una distribución más de cerca. Sin embargo, evite comparar directamente los valores AD en diferentes distribuciones cuando los valores AD son cercanos, porque los estadísticos AD se distribuyen de manera diferente para distintas distribuciones. Para comparar mejor el ajuste de diferentes distribuciones, utilice criterios adicionales, tales como las gráficas de probabilidades, los valores p y su conocimiento del proceso.
P
Nota
Ningún valor p para la prueba de AD está disponible para las distribuciones de 3 parámetros, excepto por la distribución de Weibull.
Interpretación
Utilice el valor p para evaluar el ajuste de la distribución.
- P ≤ α: Los datos no siguen la distribución (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que sus datos no siguen la distribución.
- P > α: No puede concluir que los datos no siguen la distribución (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. No existe suficiente evidencia para concluir que los datos no siguen la distribución. Usted puede presuponer que los datos siguen la distribución.
- Elija la distribución que se utiliza más frecuentemente en su industria o aplicación.
- Elija la distribución que proporcione los resultados más conservadores. Por ejemplo, si usted realiza un análisis de capacidad, puede realizar el análisis utilizando diferentes distribuciones y luego elegir la distribución que produzca los índices de capacidad más conservadores. Para obtener más información, vaya a Percentiles de distribución para Identificación de distribución individual y haga clic en "Porcentajes y percentiles".
- Elija la distribución más simple que se ajuste adecuadamente a sus datos. Por ejemplo, si tanto una distribución de 2 parámetros como otra de 3 parámetros proporcionan un buen ajuste, usted podría elegir la distribución más simple de 2 parámetros.
Important
Interprete los resultados de una muestra muy pequeña o muy grande con precaución. Si tiene una muestra muy pequeña, una prueba de bondad de ajuste pudiera no tener suficiente potencia para detectar alejamientos significativos de la distribución. Si tiene una muestra muy grande, la prueba pudiera tener tanta potencia que detecte alejamientos incluso pequeños de la distribución que no tengan significancia práctica. Utilice las gráficas de probabilidad, además de los valores p, para evaluar el ajuste de distribución.
Prueba de bondad del ajuste
| Distribución | AD | P | LRT P |
|---|---|---|---|
| Normal | 0.754 | 0.046 | |
| Transformación Box-Cox | 0.414 | 0.324 | |
| Lognormal | 0.650 | 0.085 | |
| Lognormal de 3 parámetros | 0.341 | * | 0.017 |
| Exponencial | 20.614 | <0.003 | |
| Exponencial de 2 parámetros | 1.684 | 0.014 | 0.000 |
| Weibull | 1.442 | <0.010 | |
| Weibull de 3 parámetros | 0.230 | >0.500 | 0.000 |
| Valor extremo más pequeño | 1.656 | <0.010 | |
| Valor extremo por máximos | 0.394 | >0.250 | |
| Gamma | 0.702 | 0.071 | |
| Gamma de 3 parámetros | 0.268 | * | 0.006 |
| Logística | 0.726 | 0.034 | |
| Loglogística | 0.659 | 0.050 | |
| Loglogística de 3 parámetros | 0.432 | * | 0.027 |
| Transformación de Johnson | 0.124 | 0.986 |
En estos resultados, varias distribuciones tienen un valor p mayor que 0.05. La distribución de Weibull de 3 parámetros (P > 0.500) y la distribución de valor extremo más grande (P > 0.250) tienen los mayores valores p y parecen ajustarse a los datos de la muestra mejor que las demás distribuciones. Además, la transformación de Box-Cox (P = 0.324) y la transformación de Johnson (P = 0.986) son efectivas al transformar los datos para que sigan una distribución normal.
Nota
Para varias distribuciones, Minitab también muestra los resultados de la distribución con un parámetro adicional. Por ejemplo, para la distribución lognormal, Minitab muestra los resultados de las versiones tanto de 2 parámetros como de 3 parámetros de la distribución. Para distribuciones que tienen parámetros adicionales, utilice el valor p para la prueba de relación de verosimilitud (LRT P) a fin de determinar si agregar otro parámetro mejora significativamente el ajuste de la distribución. Un valor p para LRT menor que 0.05 sugiere que la mejora en el ajuste es significativa. Para obtener más información, véase la sección sobre LRT P.
LRT P
Para varias distribuciones, Minitab también muestra los resultados de la distribución con un parámetro adicional. Para cada versión de una distribución con un parámetro adicional, Minitab indica un valor p para la prueba de relación de verosimilitud (LRT P). Un valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Para la prueba de relación de verosimilitud en identificación de distribución individual, la hipótesis nula es que los datos siguen la distribución más pequeña (parámetro más bajo). Por lo tanto, valores p para LRT más bajos proporcionan fuerte evidencia de que el ajuste de distribución mejora significativamente al utilizar un parámetro adicional.
Interpretación
Utilice el valor p para LRT para determinar si la adición del parámetro extra mejora significativamente el ajuste respecto a la distribución sin el parámetro extra.
- P ≤ α: La distribución más grande (parámetro más alto) proporciona un ajuste significativamente mejor. (Rechazar H0)
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula y concluye que el ajuste de distribución mejoró significativamente al usar un parámetro adicional.
- P > α: No puede concluir que la distribución más grande (parámetro más alto) proporciona un ajuste significativamente mejor (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula. No hay suficiente evidencia para concluir que el ajuste de distribución mejoró significativamente al utilizar un parámetro adicional.
El valor p para LRT también es útil para distribuciones de 3 parámetros para las cuales no existe un método establecido para calcular el valor p. En estos casos, examine primero el valor p de la distribución de 2 parámetros correspondiente. Luego examine el valor p para LRT de la distribución de 3 parámetros para determinar si la distribución de 3 parámetros es significativamente mejor que la distribución de 2 parámetros.
En estos resultados, los valores p para LRT para las distribuciones lognormal de 3 parámetros (0.017), Weibull de 3 parámetros (0.000), gamma de 3 parámetros (0.006) y loglogística de 3 parámetros (0.027) sugieren que estas distribuciones mejoran significativamente el ajuste en comparación con sus contrapartes de 2 parámetros.
Prueba de bondad del ajuste
| Distribución | AD | P | LRT P |
|---|---|---|---|
| Normal | 0.754 | 0.046 | |
| Transformación Box-Cox | 0.414 | 0.324 | |
| Lognormal | 0.650 | 0.085 | |
| Lognormal de 3 parámetros | 0.341 | * | 0.017 |
| Exponencial | 20.614 | <0.003 | |
| Exponencial de 2 parámetros | 1.684 | 0.014 | 0.000 |
| Weibull | 1.442 | <0.010 | |
| Weibull de 3 parámetros | 0.230 | >0.500 | 0.000 |
| Valor extremo más pequeño | 1.656 | <0.010 | |
| Valor extremo por máximos | 0.394 | >0.250 | |
| Gamma | 0.702 | 0.071 | |
| Gamma de 3 parámetros | 0.268 | * | 0.006 |
| Logística | 0.726 | 0.034 | |
| Loglogística | 0.659 | 0.050 | |
| Loglogística de 3 parámetros | 0.432 | * | 0.027 |
| Transformación de Johnson | 0.124 | 0.986 |
