Métodos y fórmulas para la Gráfica de observaciones individuales

Puntos graficados

Cada uno de los puntos de los datos, x_i, es una observación.

Línea central

La línea central representa la media del proceso, μ. Si usted no especifica un valor histórico para la media del proceso, Minitab utiliza la media de las observaciones.

Límites de control

Si usted no especifica un valor histórico para la desviación estándar del proceso, σ, entonces Minitab estima σ a partir de los datos utilizando el método especificado.

Límite de control inferior (LCI)

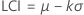
Límite de control superior (LCS)

Notación

Término	Description
μ	media del proceso
k	parámetro para la Prueba 1. El valor predeterminado es 3.

Límites de control extendidos: Enfoque entre/dentro

Utiliza el enfoque entre/dentro para calcular límites de control extendidos a partir de la variación estándar entre subgrupos y subgrupos internos.

Tamaño del subgrupo= 1

Donde u_I y_{u O} son cuantiles de la distribución normal estandarizada.

Para el cuadrado medio esperado, calcular σ̂_O de la siguiente manera:

Notación para el enfoque entre/dentro

Término	Description
μ̂	estimación de la media del proceso
σ̂_I	Estimación de la desviación estándar dentro del subgrupo
σ̂_O	Estimación de la desviación estándar entre subgrupos. Si solo hay 1 subgrupo, entonces σ̂_O = 0.
n	longitud del rango móvil cuando el tamaño del subgrupo es 1
α_I	Probabilidad de falsa alarma para la desviación estándar dentro del subgrupo
Φ^-1	la función de distribución acumulada inversa de la distribución normal estándar
α_O	Probabilidad de falsa alarma para desviación estándar entre subgrupos
MS_S	el cuadrado medio asociado a la variación de subgrupo a subgrupo
MSE	cuadrado medio del error. El cuadrado medio dentro del subgrupo se restó al cuadrado medio del subgrupo antes de estimar el componente de desviación estándar entre subgrupos.
C	coeficiente para el cuadrado medio esperado para subgrupos como factor aleatorio. Para los cálculos de cuadrados medios esperados y para información sobre modelos desequilibrados o más complejos, véase Montgomery¹ y Neter². D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons. J. Neter, W. Wasserman y M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Límites de control extendidos: Aproximación mínima/máxima media

Utiliza el enfoque de la media mínima/máxima para calcular límites de control extendidos a partir de las medias mínima y máxima de grupo.

Tamaño del subgrupo= 1

Donde u_I es el cuantil de la distribución normal estandarizada.

Para el m subgrupo más grande significa:

Para el m subgrupo más pequeño significa:

Notación para el enfoque mínimo/máximo

Término	Description
μ̂	estimación de la media del proceso
μ̂_max	estimación de la media máxima del proceso. Usando la longitud del rango móvil como tamaño del subgrupo, esta estimación es el promedio ponderado de las `m` medias del subgrupo más grande. Si el análisis especifica usar más subgrupos de los que hay en los datos, `m` es el número de subgrupos.
μ̂_min	estimación de la media mínima del proceso. Usando la longitud del rango móvil como tamaño del subgrupo, esta estimación es la media ponderada de las `m` medias del subgrupo más pequeño. Si el análisis especifica usar más subgrupos de los que hay en los datos, `m` es el número de subgrupos.
m	Número de medias de subgrupos para promediar
σ̂_I	Estimación de la desviación estándar dentro del subgrupo
n	longitud del rango móvil cuando el tamaño del subgrupo es 1
Φ^-1	la función de distribución acumulada inversa de la distribución normal estándar
α_I	Probabilidad de falsa alarma para la desviación estándar dentro del subgrupo

Desviación estándar para límites extendidos

Cuando se seleccionan límites extendidos, utiliza la siguiente desviación estándar para valores de variación almacenados y límites sigma adicionales.

Método del promedio de rango móvil

El promedio de rango móvil, , de longitud w viene dado por la siguiente fórmula:

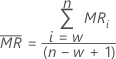
donde MR_i es el rango móvil de la observación i, que se calcula de la siguiente manera:

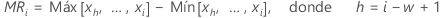
Minitab utiliza para calcular S_mr, que es una estimación sin sesgo de σ:

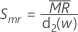
Notación

Término	Description
n	número de observaciones
w	longitud del rango móvil. El valor predeterminado es 2.
d₂()	valor de la constante de eliminación de sesgo d₂, que corresponde al valor especificado entre paréntesis.

Estimación de Nelson

Utilice la estimación de Nelson para corregir valores de rangos móviles extrañamente grandes en el cálculo de los límites de control. El procedimiento es similar al propuesto por Nelson¹ Minitab elimina cualquier valor de rango móvil que sea más de 3 σ mayor que el rango móvil promedio, luego vuelve a calcular el promedio de rango móvil y los límites de control.

Método de la mediana de rango móvil

La mediana de rango móvil, , de longitud w viene dada por la siguiente fórmula:

donde MR_i es el rango móvil de la observación i, que se calcula de la siguiente manera:

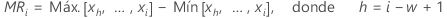
Minitab utiliza para calcular S_mr, que es una estimación sin sesgo de σ:

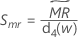
Notación

Término	Description
n	número de observaciones
w	longitud del rango móvil. El valor predeterminado es 2.
d₄()	valor de la constante de eliminación de sesgo d₄, que corresponde al valor especificado entre paréntesis.

Método de la raíz cuadrada de MSSD

MSSD significa media de las diferencias sucesivas cuadráticas. La raíz cuadrada de la MSSD (SRMSSD) se calcula de la siguiente manera:

Con constante de eliminación de sesgo

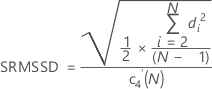
Sin constante de eliminación de sesgo

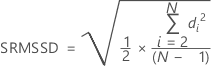
Notación

Término	Description
d_i	diferencia entre el valor de observación i y el valor de observación i – 1
N	número de observaciones
c₄'(N)	constante de eliminación de sesgo tomada de una tabla

Constantes de eliminación de sesgo d2(), d3() y d4()

d₂(N) es el valor esperado del rango de N observaciones de una población normal con desviación estándar = 1. Por lo tanto, si r es el rango de una muestra de N observaciones de una distribución normal con desviación estándar = σ, entonces E(r) = d₂(N)σ.

d₃(N) es la desviación estándar del rango de N observaciones de una población normal con σ = 1. Por lo tanto, si r es el rango de una muestra de N observaciones de una distribución normal con una desviación estándar = σ, entonces desv.est.(r) = d₃(N)σ.

Utilice la siguiente tabla para hallar una constante de eliminación de sesgo para un valor dado, N. (Para determinar el valor de N, consulte la fórmula del estadístico de interés.)

Para valores de N de 51 a 100, utilice la siguiente aproximación para d₂(N):

Para valores de N de 26 a 100, utilice las siguientes aproximaciones para d₃(N) y d₄(N):

Para obtener más información sobre estas constantes, consulte lo siguiente:

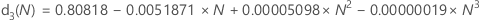
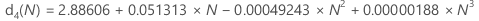
D. J. Wheeler y D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.

Table 1. Tabla de valores
N	d₂(N)	d₃(N)	d₄(N)
2	1.128	0.8525	0.954
3	1.693	0.8884	1.588
4	2.059	0.8798	1.978
5	2.326	0.8641	2.257
6	2.534	0.8480	2.472
7	2.704	0.8332	2.645
8	2.847	0.8198	2.791
9	2.970	0.8078	2.915
10	3.078	0.7971	3.024
11	3.173	0.7873	3.121
12	3.258	0.7785	3.207
13	3.336	0.7704	3.285
14	3.407	0.7630	3.356
15	3.472	0.7562	3.422
16	3.532	0.7499	3.482
17	3.588	0.7441	3.538
18	3.640	0.7386	3.591
19	3.689	0.7335	3.640
20	3.735	0.7287	3.686
21	3.778	0.7242	3.730
22	3.819	0.7199	3.771
23	3.858	0.7159	3.811
24	3.895	0.7121	3.847
25	3.931	0.7084	3.883

N	d₂(N)
26	3.964
27	3.997
28	4.027
29	4.057
30	4.086
31	4.113
32	4.139
33	4.165
34	4.189
35	4.213
36	4.236
37	4.259
38	4.280
39	4.301
40	4.322
41	4.341
42	4.361
43	4.379
44	4.398
45	4.415
46	4.433
47	4.450
48	4.466
49	4.482
50	4.498

Constante de eliminación de sesgo c4'()

Utilice las siguientes tablas para hallar valores para la constante de eliminación de sesgo, c₄'(), que se usa en las fórmulas para la raíz cuadrada del método MSSD para estimar sigma.

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
2	0.797850	41	0.990797	80	0.995215
3	0.871530	42	0.991013	81	0.995272
4	0.905763	43	0.991218	82	0.995328
5	0.925222	44	0.991415	83	0.995383
6	0.937892	45	0.991602	84	0.995436
7	0.946837	46	0.991782	85	0.995489
8	0.953503	47	0.991953	86	0.995539
9	0.958669	48	0.992118	87	0.995589
10	0.962793	49	0.992276	88	0.995638
11	0.966163	50	0.992427	89	0.995685
12	0.968968	51	0.992573	90	0.995732
13	0.971341	52	0.992713	91	0.995777
14	0.973375	53	0.992848	92	0.995822
15	0.975137	54	0.992978	93	0.995865
16	0.976679	55	0.993103	94	0.995908
17	0.978039	56	0.993224	95	0.995949
18	0.979249	57	0.993340	96	0.995990
19	0.980331	58	0.993452	97	0.996030
20	0.981305	59	0.993561	98	0.996069
21	0.982187	60	0.993666	99	0.996108
22	0.982988	61	0.993767	100	0.996145
23	0.983720	62	0.993866	101	0.996182
24	0.984391	63	0.993961	102	0.996218
25	0.985009	64	0.994053	103	0.996253
26	0.985579	65	0.994142	104	0.996288
27	0.986107	66	0.994229	105	0.996322
28	0.986597	67	0.994313	106	0.996356
29	0.987054	68	0.994395	107	0.996389
30	0.987480	69	0.994474	108	0.996421
31	0.987878	70	0.994551	109	0.996452
32	0.988252	71	0.994626	110	0.996483
33	0.988603	72	0.994699	111	0.996514
34	0.988934	73	0.994769	112	0.996544
35	0.989246	74	0.994838	113	0.996573
36	0.989540	75	0.994905	114	0.996602
37	0.989819	76	0.994970	115	0.996631
38	0.990083	77	0.995034	116	0.996658
39	0.990333	78	0.995096	117	0.996686
40	0.990571	79	0.995156	118	0.996713

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
119	0.996739	160	0.997541	201	0.998016
120	0.996765	161	0.997555	202	0.998025
121	0.996791	162	0.997570	203	0.998034
122	0.996816	163	0.997584	204	0.998043
123	0.996841	164	0.997598	205	0.998052
124	0.996865	165	0.997612	206	0.998061
125	0.996889	166	0.997625	207	0.998070
126	0.996913	167	0.997639	208	0.998078
127	0.996936	168	0.997652	209	0.998087
128	0.996959	169	0.997665	210	0.998095
129	0.996982	170	0.997678	211	0.998104
130	0.997004	171	0.997691	212	0.998112
131	0.997026	172	0.997703	213	0.998120
132	0.997047	173	0.997716	214	0.998128
133	0.997069	174	0.997728	215	0.998137
134	0.997089	175	0.997741	216	0.998145
135	0.997110	176	0.997753	217	0.998152
136	0.997130	177	0.997765	218	0.998160
137	0.997150	178	0.997776	219	0.998168
138	0.997170	179	0.997788	220	0.998176
139	0.997189	180	0.997800	221	0.998184
140	0.997209	181	0.997811	222	0.998191
141	0.997227	182	0.997822	223	0.998199
142	0.997246	183	0.997834	224	0.998206
143	0.997264	184	0.997845	225	0.998214
144	0.997282	185	0.997856	226	0.998221
145	0.997300	186	0.997866	227	0.998228
146	0.997318	187	0.997877	228	0.998235
147	0.997335	188	0.997888	229	0.998242
148	0.997352	189	0.997898	230	0.998250
149	0.997369	190	0.997909	231	0.998257
150	0.997386	191	0.997919	232	0.998263
151	0.997402	192	0.997929	233	0.998270
152	0.997419	193	0.997939	234	0.998277
153	0.997435	194	0.997949	235	0.998284
154	0.997450	195	0.997959	236	0.998291
155	0.997466	196	0.997969	237	0.998297
156	0.997481	197	0.997978	238	0.998304
157	0.997497	198	0.997988	239	0.998311
158	0.997512	199	0.997997	240	0.998317
159	0.997526	200	0.998007	241	0.998323

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
242	0.998330	283	0.998553	324	0.998720
243	0.998336	284	0.998558	325	0.998723
244	0.998342	285	0.998562	326	0.998727
245	0.998349	286	0.998567	327	0.998730
246	0.998355	287	0.998571	328	0.998734
247	0.998361	288	0.998576	329	0.998737
248	0.998367	289	0.998580	330	0.998740
249	0.998373	290	0.998585	331	0.998744
250	0.998379	291	0.998589	332	0.998747
251	0.998385	292	0.998593	333	0.998751
252	0.998391	293	0.998598	334	0.998754
253	0.998397	294	0.998602	335	0.998757
254	0.998403	295	0.998606	336	0.998761
255	0.998408	296	0.998611	337	0.998764
256	0.998414	297	0.998615	338	0.998767
257	0.998420	298	0.998619	339	0.998770
258	0.998425	299	0.998623	340	0.998774
259	0.998431	300	0.998627	341	0.998777
260	0.998436	301	0.998632	342	0.998780
261	0.998442	302	0.998636	343	0.998783
262	0.998447	303	0.998640	344	0.998786
263	0.998453	304	0.998644	345	0.998790
264	0.998458	305	0.998648	346	0.998793
265	0.998463	306	0.998652	347	0.998796
266	0.998469	307	0.998656	348	0.998799
267	0.998474	308	0.998660	349	0.998802
268	0.998479	309	0.998664	350	0.998805
269	0.998484	310	0.998668	351	0.998808
270	0.998489	311	0.998671	352	0.998811
271	0.998495	312	0.998675	353	0.998814
272	0.998500	313	0.998679	354	0.998817
273	0.998505	314	0.998683	355	0.998820
274	0.998510	315	0.998687	356	0.998823
275	0.998515	316	0.998690	357	0.998826
276	0.998519	317	0.998694	358	0.998829
277	0.998524	318	0.998698	359	0.998832
278	0.998529	319	0.998701	360	0.998835
279	0.998534	320	0.998705	361	0.998837
280	0.998539	321	0.998709	362	0.998840
281	0.998544	322	0.998712	363	0.998843
282	0.998548	323	0.998716	364	0.998846

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
365	0.998849	411	0.998963	457	0.999054
366	0.998851	412	0.998965	458	0.999056
367	0.998854	413	0.998967	459	0.999058
368	0.998857	414	0.998970	460	0.999060
369	0.998860	415	0.998972	461	0.999061
370	0.998862	416	0.998974	462	0.999063
371	0.998865	417	0.998976	463	0.999065
372	0.998868	418	0.998978	464	0.999067
373	0.998871	419	0.998980	465	0.999068
374	0.998873	420	0.998982	466	0.999070
375	0.998876	421	0.998985	467	0.999072
376	0.998879	422	0.998987	468	0.999073
377	0.998881	423	0.998989	469	0.999075
378	0.998884	424	0.998991	470	0.999077
379	0.998886	425	0.998993	471	0.999078
380	0.998889	426	0.998995	472	0.999080
381	0.998892	427	0.998997	473	0.999082
382	0.998894	428	0.998999	474	0.999084
383	0.998897	429	0.999001	475	0.999085
384	0.998899	430	0.999003	476	0.999087
385	0.998902	431	0.999005	477	0.999088
386	0.998904	432	0.999007	478	0.999090
387	0.998907	433	0.999009	479	0.999092
388	0.998909	434	0.999011	480	0.999093
389	0.998912	435	0.999013	481	0.999095
390	0.998914	436	0.999015	482	0.999097
391	0.998917	437	0.999017	483	0.999098
392	0.998919	438	0.999019	484	0.999100
393	0.998921	439	0.999021	485	0.999101
394	0.998924	440	0.999023	486	0.999103
395	0.998926	441	0.999025	487	0.999104
396	0.998929	442	0.999027	488	0.999106
397	0.998931	443	0.999028	489	0.999108
398	0.998933	444	0.999030	490	0.999109
399	0.998936	445	0.999032	491	0.999111
400	0.998938	446	0.999034	492	0.999112
401	0.998940	447	0.999036	493	0.999114
402	0.998943	448	0.999038	494	0.999115
403	0.998945	449	0.999040	495	0.999117
404	0.998947	450	0.999042	496	0.999118
405	0.998950	451	0.999043	497	0.999120
406	0.998952	452	0.999045	498	0.999121
407	0.998954	453	0.999047	499	0.999123
408	0.998956	454	0.999049	500	0.999124
409	0.998959	455	0.999051
410	0.998961	456	0.999052

Box-Cox

Fórmula de Box-Cox

Si se utiliza una transformación de Box-Cox, Minitab transforma los valores originales de los datos (Y_i) según la siguiente fórmula:

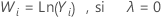
donde λ es el parámetro de la transformación. Minitab crea entonces un gráfico de control con los valores de datos transformados (W_i). Para saber cómo Minitab elige el valor óptimo para λ, ve a Métodos y fórmulas para Transformación de Box-Cox.

Valores comunes de λ

La siguiente tabla muestra algunos valores de λ utilizados comúnmente y sus transformaciones.

λ	Transformación
2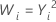
0.5
0
-0.5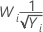
-1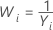

Métodos y fórmulas para la Gráfica de observaciones individuales

En este tema

Puntos graficados

Línea central

Límites de control

Límite de control inferior (LCI)

Límite de control superior (LCS)

Notación

Límites de control extendidos: Enfoque entre/dentro

Notación para el enfoque entre/dentro

Límites de control extendidos: Aproximación mínima/máxima media

Notación para el enfoque mínimo/máximo

Desviación estándar para límites extendidos

Método del promedio de rango móvil

Notación

Estimación de Nelson

Método de la mediana de rango móvil

Notación

Método de la raíz cuadrada de MSSD

Con constante de eliminación de sesgo

Sin constante de eliminación de sesgo

Notación

Constantes de eliminación de sesgo d2(), d3() y d4()

Constante de eliminación de sesgo c4'()

Box-Cox

Fórmula de Box-Cox

Valores comunes de λ