Seleccione el método o la fórmula de su preferencia.
En este tema
Puntos graficados
Datos en subgrupos
Cuando los datos están en subgrupos, T2 se calcula de la siguiente manera:
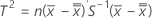
donde:
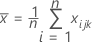
 es el vector medio de
es el vector medio de 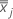 (media de xjk valores), que se calcula de la siguiente manera:
(media de xjk valores), que se calcula de la siguiente manera:
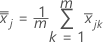
S = matriz de covarianzas de la muestra
La matriz de covarianzas de la muestra, S, se calcula de la siguiente manera:

donde:
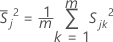
donde:
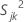 , la varianza muestral para la característica jésima en la késima muestra, se calcula como sigue:
, la varianza muestral para la característica jésima en la késima muestra, se calcula como sigue:
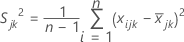
donde:
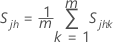
donde:
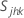 , la covarianza, =
, la covarianza, =
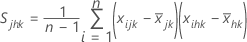
El promedio de las matrices S es una estimación sin sesgo de la varianza cuando el proceso está bajo control. n debe ser mayor que p y no debe haber correlaciones fuertes entre las variables, de forma que la matriz de covarianzas de la muestra no sea singular.
Cuando los datos están en subgrupos, el gráfico muestra un valor faltante para cualquier subgrupo que sea una observación individual.
Observaciones individuales
Cuando los datos son observaciones individuales, T2 se calcula de la siguiente manera:
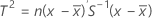
donde:
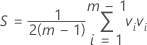
donde:

Notación
| Término | Description |
|---|---|
| n | tamaño de la muestra |
 | vector medio de la muestra |
| Xijk | La i-ésima observación sobre la característica j-ésima en la k-ésima muestra |
| m | número de muestras |
Ejemplo de cómo calcular T2
Minitab grafica el estadístico T2 en una gráfica de control. Si un punto graficado excede los límites de control, el proceso está fuera de control en ese punto. Véase la tabla y ecuaciones de la muestra como referencia en los cálculos de Minitab.
Los siguientes datos provienen de un proceso de desarrollo de una solución de limpieza. Las cantidades de citrato de sodio y glicerina afectan la potencia de la solución.
| Medias de subgrupo | Varianzas y covarianzas | Estadístico T2 | ||||
| Subgrupo | Citrato de sodio (X1) | Glicerina (X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| Promedios | 7875 | 2333 | 7931 | 9318 | 3003 | |
- Calcule las medias de los subgrupos para cada variable, X1 y X2. En este caso, cada subgrupo tenía cuatro muestras.
- Si usted tiene observaciones individuales, Minitab las utiliza en lugar de las medias de los subgrupos en todos los cálculos.
- Calcule las varianzas de los subgrupos S1 2 y S2 2.
- Calcule las covarianzas de los subgrupos S1 2 k.
- Calcule las medias de las medias de los subgrupos, las medias de las varianzas de los subgrupos y la media de las covarianzas.
- Designe la matriz S de covarianza de la muestra y el vector medio.
- Calcule T2, que viene dada por:
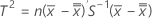
Minitab grafica T2 en la gráfica T2 y la compara con los límites de control para determinar si los puntos individuales están fuera de control.
Línea central
La línea central de la gráfica T2 es KX. El cálculo de K y X depende del máximo tamaño de las muestras y de si Minitab estima la matriz de covarianzas a partir de los datos.
Datos en subgrupos
Cuando los datos están en subgrupos, KX se calcula de la siguiente manera:
- Dada la matriz de covarianzas
-


- Matriz de covarianzas estimada
-


Observaciones individuales
Cuando los datos son observaciones individuales, KX se calcula de la siguiente manera:
- Dada la matriz de covarianzas
-
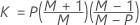
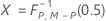
- Matriz de covarianzas estimada
-
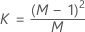
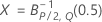
donde:
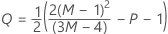
Notación
| Término | Description |
|---|---|
| P | número de variables |
| M | número de subgrupos |
| N | tamaño de la muestra |
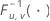 | la distribución F acumulada inversa con u grados de libertad del numerador y v grados de libertad del denominador |
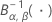 | la distribución beta acumulada inversa con el primer parámetro de forma α y el segundo parámetro de forma β |
Límite de control
Datos en subgrupos
El límite de control superior si usted no especifica parámetros es:
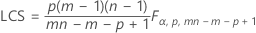
El límite de control superior si usted especifica parámetros es:
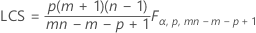
Observaciones individuales
El límite de control superior si usted no especifica parámetros es:
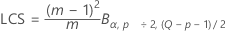
donde:
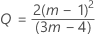
Véase Woodall et al.1 para obtener más información.
El límite de control superior si usted especifica parámetros es:
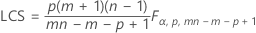
Notación
| Término | Description |
|---|---|
| α | valor fijo de 0.00134989803156746 |
| p | número de características |
| m |
Para datos en subgrupos, si usted no especifica las estimaciones de los parámetros, entonces m es el número de muestras. Si proporciona las estimaciones de los parámetros, entonces m es el número de muestras utilizadas para crear la matriz de covarianza. Para datos individuales, m es el número de observaciones. |
| n | tamaño de cada muestra |
| F | indica que se utiliza la distribución F |
| B | indica que se utiliza la distribución beta |
Estadístico de T2 descompuesta
Estadístico de T2 descompuesta:
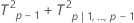
donde:

donde:
xi(p − 1)es el vector medio descompuesto
Sxx es la submatriz principal (p – 1) × (p – 1) de S
T2p|1,..., p−1 es una aproximación que difiere por fases y si usted tiene subgrupos u observaciones individuales:
Fase 1 para datos en subgrupos:
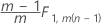
Fase 2 para datos en subgrupos:
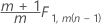
Fase 1 para observaciones individuales:
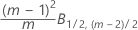
Fase 2 para observaciones individuales:
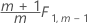
Minitab calcula los límites de control de la fase 1 cuando usted no especifica las estimaciones de los parámetros y los límites de control de la fase 2 cuando sí los especifica.
Véase Mason et al.2 para obtener más información sobre el estadístico de T2 descompuesta.
Notación
| Término | Description |
|---|---|
| m | número de muestras |
| F | indica que se utiliza la distribución F |
| B | indica que se utiliza la distribución beta |
Métodos y fórmulas para Box-Cox
Fórmula de Box-Cox
Si usted utiliza una transformación de Box-Cox, Minitab transforma los valores de los datos originales (Yi) de acuerdo con la siguiente fórmula:

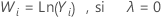
donde λ es el parámetro de la transformación. Luego Minitab crea una gráfica de control con los valores de los datos transformados (Wi). Para enterarse de cómo Minitab elige el valor óptimo para λ, vaya a Métodos y fórmulas para Transformación de Box-Cox.
Valores comunes de λ
| λ | Transformación |
|---|---|
| 2 | 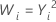 |
| 0.5 |  |
| 0 |  |
| −0.5 | 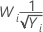 |
| −1 | 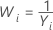 |
