Métodos y fórmulas para la Gráfica de varianza generalizada

|S_i|, que es el determinante de la matriz de covarianza muestral para la muestra i.

Si no hay subgrupos, no se pueden calcular todas las fórmulas de la gráfica de varianza generalizada. En este caso, Minitab estandariza todos los valores restando la media de la columna adecuada y luego dividiendo entre la raíz cuadrada de la varianza adecuada de la matriz de covarianzas de todos los datos.

Cuando los datos están en subgrupos, el gráfico muestra un valor faltante para cualquier subgrupo que sea una observación individual. El gráfico también muestra un valor que falta si el tamaño de un subgrupo es menor o igual que el número de variables del gráfico.

Ver Montgomery¹ para obtener más información sobre las gráficas de varianza generalizada.

Límite de control inferior (LCI)

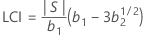
donde:

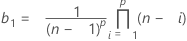
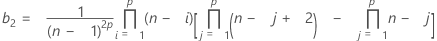
El valor mínimo del LCI es 0.

Límite de control superior (LCS)

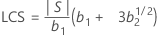
Notación

Fórmula de Box-Cox

Si usted utiliza una transformación de Box-Cox, Minitab transforma los valores de los datos originales (Y_i) de acuerdo con la siguiente fórmula:

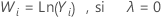
donde λ es el parámetro de la transformación. Luego Minitab crea una gráfica de control con los valores de los datos transformados (W_i). Para enterarse de cómo Minitab elige el valor óptimo para λ, vaya a Métodos y fórmulas para Transformación de Box-Cox.

Valores comunes de λ

La siguiente tabla muestra algunos valores de λ utilizados comúnmente y sus transformaciones.

λ	Transformación
2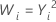
0.5
0
−0.5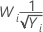
−1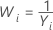