En este tema
Gráfica Xbarra
La gráfica Xbarra representa el promedio de las mediciones dentro de cada subgrupo. La línea central es el promedio de todos los promedios de los subgrupos. Los límites de control, que se establecen a una distancia de 3 desviaciones estándar por encima y por debajo de la línea central, muestran la cantidad de variación esperada en los promedios de los subgrupos.
Minitab muestra una gráfica Xbarra cuando el tamaño del subgrupo es mayor que 1.
Interpretación
Utilice una gráfica Xbarra para monitorear la media de un proceso y determinar si es lo suficientemente estable como para realizar un análisis de capacidad.
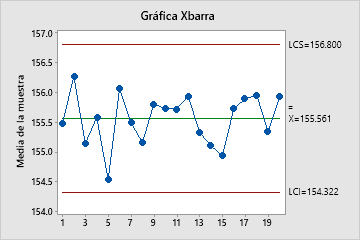
En estos resultados, los puntos varían de manera aleatoria alrededor de la línea central y se encuentran dentro de los límites de control. No se observan tendencias ni patrones. El centro del proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Gráfica I
La gráfica I representa las observaciones individuales. La línea central es una estimación del promedio del proceso. Los límites de control, que se establecen a una distancia de 3 desviaciones estándar por encima y por debajo de la línea central, muestran la cantidad de variación esperada en los valores individuales de la muestra.
Minitab muestra una gráfica I cuando el tamaño del subgrupo es 1.
Interpretación
Utilice una gráfica I para evaluar si las mediciones individuales están bajo control y determinar si el proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Los puntos rojos indican observaciones que no pasan al menos una de las pruebas para detectar causas especiales y no están bajo control. Los puntos fuera de control indican que el proceso pudiera no ser estable y que los resultados de un análisis de capacidad podrían no ser fiables. Usted debe identificar la causa de los puntos fuera de control y eliminar cualquier variación por causas especiales antes de analizar la capacidad del proceso.
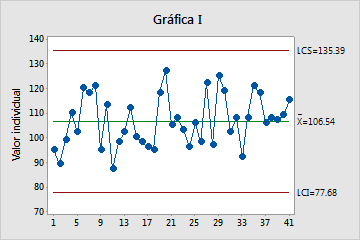
En esta gráfica, los puntos varían de manera aleatoria alrededor de la línea central y se encuentran dentro de los límites de control. No se observan tendencias ni patrones. El centro del proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Gráfica R
La gráfica R representa los rangos de los subgrupos. Si el tamaño de los subgrupos es constante, entonces la línea central es el promedio de todos los rangos de subgrupos. Si los tamaños de los subgrupos difieren, entonces el valor de la línea central depende del tamaño del subgrupo, porque subgrupos más grandes tienden a tener rangos más grandes. Los límites de control, que se encuentran a una distancia de 3 desviaciones estándar por encima y por debajo de la línea central, muestran la cantidad de variación esperada en los rangos de los subgrupos.
Minitab muestra una gráfica R para monitorear la variación si el tamaño del subgrupo es mayor que 2, pero menor que 9.
Interpretación
Utilice una gráfica R para monitorear la variación de un proceso y determinar si es lo suficientemente estable como para realizar un análisis de capacidad. La gráfica R indica si la variación entre los subgrupos está bajo control.
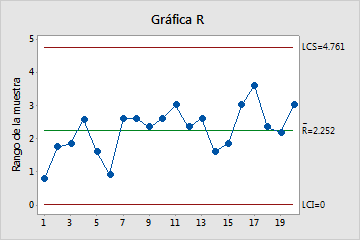
En estos resultados, los puntos varían de manera aleatoria alrededor de la línea central y se encuentran dentro de los límites de control. No se observan tendencias ni patrones. La variación del proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Gráfica S
La gráfica S representa las desviaciones estándar de los subgrupos. La línea central es el promedio de todas las desviaciones estándar de los subgrupos. Los límites de control, que se establecen a una distancia de 3 desviaciones estándar por encima y por debajo de la línea central, muestran la cantidad de variación esperada en las desviaciones estándar de los subgrupos.
Minitab muestra una gráfica S para monitorear la variación si el tamaño del subgrupo es mayor que o igual a 9.
Interpretación
Utilice una gráfica S para monitorear la variación (desviación estándar) del proceso y determinar si es lo suficientemente estable como para realizar un análisis de capacidad. La gráfica S indica si la variación entre los subgrupos está bajo control.
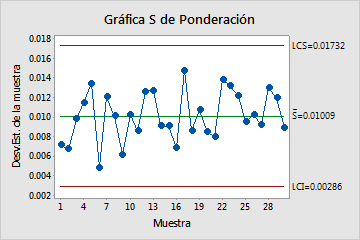
En estos resultados, los puntos varían de manera aleatoria alrededor de la línea central y se encuentran dentro de los límites de control. No se observan tendencias ni patrones. La variación del proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Gráfica de rangos móviles (MR)
La gráfica MR representa los rangos móviles de observaciones consecutivas. La línea central es el promedio de todos los rangos móviles. Los límites de control, que se encuentran a una distancia de 3 desviaciones estándar por encima y por debajo de la línea central, muestran la cantidad de variación esperada en los rangos móviles.
Minitab muestra una gráfica MR si el tamaño del subgrupo es 1.
Interpretación
Utilice una gráfica MR para monitorear la variación (rango móvil) del proceso y para determinar si es lo suficientemente estable como para realizar un análisis de capacidad. La gráfica MR indica si la variación entre las observaciones está bajo control.
Los puntos rojos indican observaciones que no pasan al menos una de las pruebas para detectar causas especiales y no están bajo control. Los puntos fuera de control indican que el proceso pudiera no ser estable y que los resultados de un análisis de capacidad podrían no ser fiables. Usted debe identificar la causa de los puntos fuera de control y eliminar cualquier variación por causas especiales antes de analizar la capacidad del proceso.
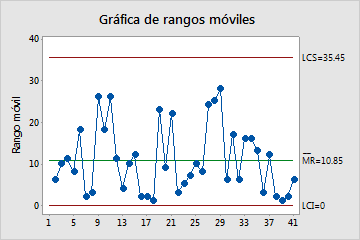
En estos resultados, los puntos varían de manera aleatoria alrededor de la línea central y se encuentran dentro de los límites de control. No se observan tendencias ni patrones. La variación del proceso es lo suficientemente estable como para realizar un análisis de capacidad.
Pruebas para detectar causas especiales
Las pruebas para detectar causas especiales evalúan si los puntos graficados en cada gráfica de control están distribuidos aleatoriamente dentro de los límites de control.
Interpretación
Utilice las pruebas para detectar causas especiales para determinar qué observaciones puede tener que investigar y para identificar patrones y tendencias en los datos. Cada una de estas pruebas para detectar causas especiales detecta un patrón o una tendencia específicos en los datos, lo que revela un aspecto diferente de la inestabilidad del proceso.
- Un punto más de 3 desviaciones estándar desde la línea central
- La Prueba 1 identifica subgrupos que son poco comunes en comparación con otros subgrupos. La prueba 1 se reconoce universalmente como una prueba necesaria para detectar situaciones fuera de control. Si pequeños cambios en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
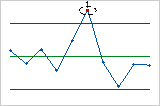
- Nueve puntos consecutivos en el mismo lado de la línea central
- La prueba 2 identifica cambios rápidos en el centrado o variación del proceso. Si pequeños cambios en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
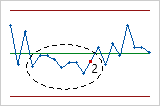
- Seis puntos consecutivos, en orden creciente o decreciente
- La Prueba 3 detecta tendencias. Esta prueba busca series largas de puntos consecutivos que de manera constante aumentan o disminuyen de valor.
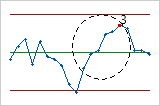
- Catorce puntos consecutivos, alternándolos arriba y abajo
- La Prueba 4 detecta variación sistemática. Usted desea que el patrón de variación en un proceso sea aleatorio, pero un punto que no pasa la Prueba 4 podría indicar que el patrón de variación es predecible.
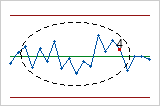
- Dos de tres puntos más de 2 desviaciones estándar desde la línea central (mismo lado)
- La Prueba 5 detecta pequeños cambios rápidos en el proceso.
- Cuatro de cinco puntos se encuentran a más de 1 desviación estándar desde la línea central (mismo lado)
- La Prueba 6 detecta pequeños cambios rápidos en el proceso.
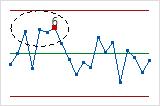
- Quince puntos consecutivos dentro de 1 desviación estándar desde la línea central (cualquier lado)
- La Prueba 7 detecta un patrón de variación que a veces se interpreta equivocadamente como evidencia de control adecuado. Esta prueba detecta límites de control que son demasiado amplios. Los límites de control que son demasiado amplios generalmente se deben a datos estratificados, lo que ocurre cuando una fuente de variación sistemática está presente dentro de cada subgrupo.
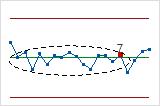
- Ocho puntos en una fila más que 1 desviación estándar desde la línea central (cualquier lado)
- La Prueba 8 detecta un patrón de mezcla. En un patrón de mezcla, los puntos tienden a ubicarse lejos de la línea central y cerca de los límites de control.
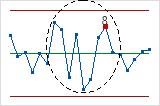
Gráfica de los últimos 25 subgrupos
La gráfica de los últimos 25 subgrupos muestra los puntos de datos de cada uno de los últimos 25 subgrupos y una línea para la media general del proceso.
Interpretación
Utilice la gráfica de los últimos 25 subgrupos para evaluar si la distribución de las observaciones dentro de los subgrupos cumple los requisitos de su análisis de capacidad.
- Un subgrupo que contenga valores atípicos
- Datos que no estén simétricamente distribuidos alrededor de la media del proceso
- Cambios en la distribución en los subgrupos
Si la gráfica muestra evidencia de problemas o cambios en los subgrupos, los resultados de capacidad pudieran no ser válidos. Investigue su proceso para determinar por qué los valores de los datos no están distribuidos aleatoriamente en los subgrupos.
En esta gráfica, los puntos parecen estar distribuidos de forma aleatoria y simétrica alrededor de la media del proceso.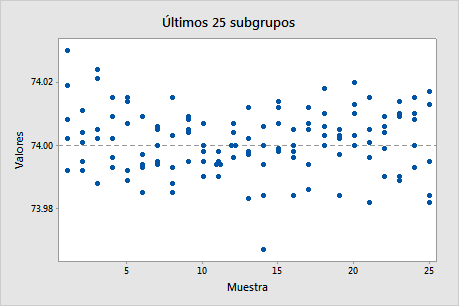
Nota
Si el tamaño de subgrupo es 1, Minitab muestra una gráfica de las últimas 25 observaciones, que se interpreta de manera similar.
Histograma de capacidad
El histograma de capacidad muestra la distribución de los datos de muestra. Cada barra del histograma representa la frecuencia de los datos dentro de un intervalo.
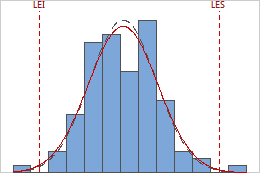Las curvas de corto plazo y general en el histograma son curvas de distribución normal que se generan utilizando la media del proceso y diferentes estimaciones de la variación del proceso. La curva de corto plazo con línea discontinua utiliza la desviación estándar dentro de los subgrupos. La curva general con línea continua utiliza la desviación estándar general. Interpretación
Utilice el histograma de capacidad para visualizar los datos de su muestra en relación con el ajuste de distribución y los límites de especificación.
Para evaluar visualmente el ajuste de distribución, compare las barras en el histograma con la línea de ajuste curva. La forma de los datos en el histograma debería coincidir aproximadamente con la curva. Para afirmar si los datos siguen la distribución, utilice los resultados en la gráfica de probabilidad.
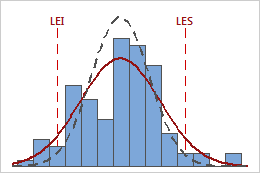
En estos resultados, los datos del proceso parecen estar bastante centrados entre los límites de especificación. Sin embargo, la dispersión del proceso es mayor que la dispersión de especificación, lo que sugiere una capacidad deficiente. Aunque la mayoría de los datos se encuentra dentro de los límites de especificación, hay partes no conformes por debajo del límite de especificación inferior (LEI) y por encima del límite de especificación superior (LES).
Nota
Para determinar el número de elementos no conformes en el proceso, utilice el resultado de PPM general.
Gráfica de probabilidad normal
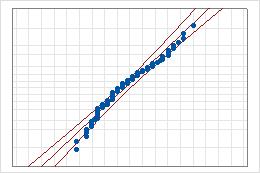
- Línea intermedia
- El percentil esperado de la distribución con base en estimaciones del parámetro de probabilidad máxima.
- Líneas de bordes de confianza
- La línea izquierda curva indica los bordes inferiores de los intervalos de confianza para los percentiles. La línea derecha curva indica los bordes superiores de los intervalos de confianza para los percentiles.
- Estadístico de la prueba de Anderson-Darling y valor p
- Los resultados de una prueba para determinar si sus datos siguen la distribución.
Interpretación
Utilice la gráfica de probabilidad normal para evaluar el requisito de que sus datos sigan una distribución normal.
Si la distribución normal provee un ajuste adecuado para los datos, los puntos forman una línea aproximadamente recta y se ubican a lo largo de la línea ajustada que se encuentra entre los bordes de confianza. Alejamientos de esta línea recta indican alejamientos de la normalidad. Si el valor p es mayor que 0.05, usted puede presuponer que los datos siguen la distribución normal. Puede evaluar la capacidad de su proceso utilizando una distribución normal.
Si el valor p es menor que 0.05, sus datos no son normales y los resultados del análisis de capacidad podrían no ser exactos. Utilice Identificación de distribución individual para determinar si debe transformar los datos o ajustar una distribución no normal para realizar el análisis de capacidad.
Gráfica de capacidad
La gráfica de capacidad se encuentra en la esquina inferior derecha del Informe de análisis de capacidad Seis en uno normal.
La gráfica de capacidad consta de tres intervalos:
- El intervalo a corto plazo representa la tolerancia potencial del proceso y se calcula multiplicando por seis la desviación estándar dentro de los subgrupos.
- El intervalo general representa la tolerancia real del proceso y se calcula multiplicando por seis la desviación estándar general.
- El intervalo de especificación representa el intervalo entre los límites de especificación inferior y superior (LEI y LES).
El centro del proceso es indicado por la marca de verificación dentro de los intervalos general y a corto plazo de la dispersión del proceso. El objetivo, si usted tiene uno, es indicado por la marca de verificación dentro de la dispersión de especificación (Espec.).
Interpretación
Utilice la gráfica de capacidad para evaluar visualmente la capacidad de su proceso.
Para evaluar la capacidad potencial de su proceso, compare la dispersión dentro del proceso con la dispersión de especificación. Para evaluar la capacidad general del proceso, compare la dispersión general del proceso con la dispersión de especificación. Si la dispersión del proceso es superior a la dispersión de especificación, su proceso necesita una mejora.
Compare el centro del proceso con el objetivo, si tiene uno. Si el proceso está centrado (sobre el objetivo), las marcas intermedias de las especificaciones y de la dispersión del proceso están alineadas verticalmente. Si el proceso no está centrado, investigue los motivos.
Si la dispersión dentro del proceso y la dispersión general del proceso difieren considerablemente, su proceso pudiera no ser estable. Revise las gráficas de control para asegurar que su proceso está bajo control.
