In This Topic
Step 1: Determine which terms contribute the most to the variability in the response
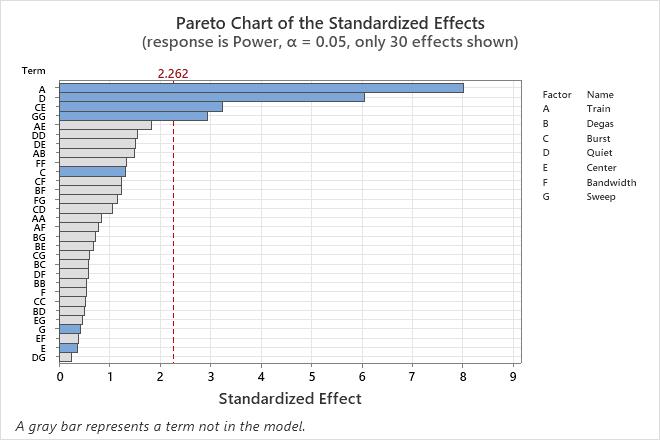
Use a Pareto chart of the standardized effects to compare the relative magnitude and the statistical significance of the effects.
Minitab plots the standardized effects in the decreasing order of their absolute values. The reference line on the chart indicates which effects are statistically significant.
Key Results: Pareto Chart
In these results, terms that are in the model have blue bars. Terms that are not in the model have gray bars. The plot shows that 2 main effects are statistically significant at the α = 0.05 significance level. A quadratic term and an interaction effect are also significant. The main effects that are parts of the interaction and the quadratic term are in the model, even though these effects are not statistically significant.
In addition, you can see that the largest effect is A because it extends the farthest. The effect for the EE quadratic term is the smallest effect on the chart.
Step 2: Determine which terms have statistically significant effects on the response
- P-value ≤ α: The association is statistically significant
- If the p-value is less than or equal to the significance level, you can conclude that there is a statistically significant association between the response variable and the term.
- P-value > α: The association is not statistically significant
- If the p-value is greater than the significance level, you cannot conclude that there is a statistically significant association between the response variable and the term. You may want to refit the model without the term.
- Factors
- If the coefficient for a factor is statistically significant, you can conclude that the coefficient for the factor does not equal 0.
- Interactions among factors
- If the coefficient for an interaction is statistically significant, you can conclude that the relationship between a factor and the response depends on the other factors in the term.
- Quadratic terms
- If the coefficient for a quadratic term is statistically significant, you can conclude that the response surface contain curvature.
- Covariates
- If the coefficient for a covariate is statistically significant, you can conclude that the association between the response and the covariate is statistically significant.
- Blocks
- If the coefficient for a block is statistically significant, you can conclude that the mean of the response values in that block is different from the overall mean of the response.
Coded Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 617.1 | 15.0 | 41.16 | 0.000 | |
| Train | 52.41 | 6.53 | 8.02 | 0.000 | 1.00 |
| Burst | 8.62 | 6.53 | 1.32 | 0.220 | 1.00 |
| Quiet | -39.59 | 6.53 | -6.06 | 0.000 | 1.00 |
| Center | -2.36 | 6.53 | -0.36 | 0.727 | 1.00 |
| Sweep | 2.84 | 6.53 | 0.44 | 0.674 | 1.00 |
| Sweep*Sweep | 49.4 | 16.7 | 2.95 | 0.016 | 1.16 |
| Burst*Center | 24.63 | 7.59 | 3.25 | 0.010 | 1.16 |
Key Results: P-Value, Coefficients
In these results, the main effects for Train and Quiet are statistically significant at the 0.05 level. You can conclude that changes in these variables are associated with changes in the response variable.
The main effect for Sweep is not statistically significant but the quadratic effect is. You can conclude that changes in this variable are associated with changes in the response variable, but the association is not linear.
The main effects for Burst and Center are not statistically significant, but the interaction effect is. You can conclude that changes in these variables are associated with changes in the response variable, but the effects depend on the other factor.
Step 3: Determine how well the model fits your data
To determine how well the model fits your data, examine the goodness-of-fit statistics in the Model Summary table.
- S
-
Use S to assess how well the model describes the response.
S is measured in the units of the response variable and represents how far the data values fall from the fitted values. The lower the value of S, the better the model describes the response. However, a low S value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
- R-sq
-
The higher the R2 value, the better the model fits your data. R2 is always between 0% and 100%.
R2 always increases when you add additional predictors to a model. For example, the best five-predictor model will always have an R2 that is at least as high as the best four-predictor model. Therefore, R2 is most useful when you compare models of the same size.
- R-sq (adj)
-
Use adjusted R2 when you want to compare models that have different numbers of predictors. R2 always increases when you add a predictor to the model, even when there is no real improvement to the model. The adjusted R2 value incorporates the number of predictors in the model to help you choose the correct model.
- R-sq (pred)
-
Use predicted R2 to determine how well your model predicts the response for new observations. Models that have larger predicted R2 values have better predictive ability.
A predicted R2 that is substantially less than R2 may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the sample data and, therefore, may not be useful for making predictions about the population.
Predicted R2 can also be more useful than adjusted R2 for comparing models because it is calculated with observations that are not included in the model calculation.
- AICc and BIC
- When you show the details for each step of a stepwise method or when you show the expanded results of the analysis, Minitab shows two more statistics. These statistics are the corrected Akaike’s Information Criterion (AICc) and the Bayesian Information Criterion (BIC). Use these statistics to compare different models. For each statistic, smaller values are desirable.
- Small samples do not provide a precise estimate of the strength of the relationship between the response and predictors. For example, f you need R2 to be more precise, you should use a larger sample (typically, 40 or more).
- Goodness-of-fit statistics are just one measure of how well the model fits the data. Even when a model has a desirable value, you should check the residual plots to verify that the model meets the model assumptions.
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 24.4482 | 93.68% | 88.77% | 76.78% |
Key Results: S, R-sq, R-sq (adj), R-sq (pred)
In these results, the model explains 93.68% of the variation. For these data, the R2 value indicates the model provides a good fit to the data. If additional models are fit with different terms, use the adjusted R2 values and the predicted R2 values to compare how well the models fit the data.
Step 4: Determine whether your model meets the assumptions of the analysis
Use the residual plots to help you determine whether the model is adequate and meets the assumptions of the analysis. If the assumptions are not met, the model may not fit the data well and you should use caution when you interpret the results.
For more information on how to handle patterns in residual plots, go to Residual plots for Analyze Definitive Screening Design and click the name of the residual plot in the list at the top of the page.
Residuals versus fits plot
The patterns in the following table may indicate that the model does not meet the model assumptions.| Pattern | What the pattern may indicate |
|---|---|
| Fanning or uneven spreading of residuals across fitted values | Nonconstant variance |
| Curvilinear | A missing higher-order term |
| A point that is far away from zero | An outlier |
| A point that is far away from the other points in the x-direction | An influential point |
Use the residuals versus fits plot to verify the assumption that the residuals are randomly distributed and have constant variance. Ideally, the points should fall randomly on both sides of 0, with no recognizable patterns in the points.
Residuals versus order plot
Trend
Shift
Cycle
Normal probability plot of the residuals
Use the normal probability plot of the residuals to verify the assumption that the residuals are normally distributed. The normal probability plot of the residuals should approximately follow a straight line.
The patterns in the following table may indicate that the model does not meet the model assumptions.
| Pattern | What the pattern may indicate |
|---|---|
| Not a straight line | Nonnormality |
| A point that is far away from the line | An outlier |
| Changing slope | An unidentified variable |
