Lag
Der Lag ist die Anzahl der Zeiträume, um die Zeitreihen miteinander versetzt sind. Die Standardanzahl der Lags reicht von (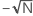
+ 10) bis (
+ 10).
Kreuzkorrelationsfunktion (CCF)
Bei der Kreuzkorrelationsfunktion handelt es sich um die Korrelation zwischen den um k Zeiteinheiten auseinander liegenden Beobachtungen von zwei Zeitreihen xt und yt (die Korrelation zwischen yt+k und xt).
Interpretation
Ermitteln Sie mit Hilfe der Kreuzkorrelationsfunktion, ob eine Beziehung zwischen zwei Zeitreihen vorliegt. Um zu ermitteln, ob eine Beziehung zwischen den beiden Zeitreihen vorliegt, suchen Sie nach einer großen Korrelation, bei der die Korrelationen auf beiden Seiten schnell in den nicht signifikanten Bereich abfallen. Eine Korrelation ist in der Regel signifikant, wenn der Absolutwert größer ist als 
, wobei n die Anzahl der Beobachtungen und k den Lag darstellt. Bei dieser Berechnung handelt es sich um ein „Faustregel“-Verfahren auf der Grundlage der approximierten Normalverteilung einer großen Stichprobe. Wenn die Kreuzkorrelation der Grundgesamtheit von Lag k für k=1, 2 ... null ist, dann ist rxy(k) für relativ große Werte von n annähernd normalverteilt mit einem Mittelwert (μ) von null und einer Standardabweichung (σ) von 1/
. Da sich ungefähr 95 % einer normalverteilten Grundgesamtheit innerhalb von 2 Standardabweichungen vom Mittelwert befinden, weist ein Test, der die Hypothese widerlegt, dass die Kreuzkorrelation der Grundgesamtheit von Lag k null entspricht, wenn | rxy(k) | größer als 2/
ist, ein Signifikanzniveau (α) von ungefähr 5 % auf.
Hinweis
Die Interpretation der Kreuzkorrelationsfunktion basiert auf der Annahme, dass keine Autokorrelation vorliegt. Weitere Informationen finden Sie unter Suchen nach Anzeichen für Autokorrelation.
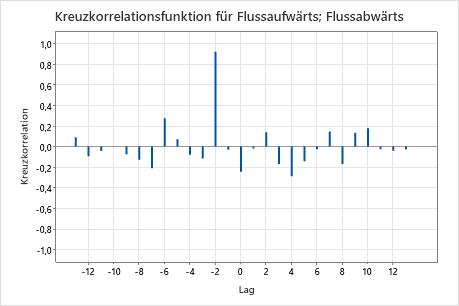
In diesem Diagramm beträgt die Korrelation bei Lag -2 ungefähr 0,92. Da 0,92 > 0,5547 = 
ist, ist die Korrelation signifikant. Sie können schlussfolgern, dass das Wasser zwei Tage benötigt, um vom flussaufwärts gelegenen Ort zum flussabwärts gelegenen Ort zu gelangen.
