In diesem Thema
Schritt 1: Bestimmen, ob die Regressionslinie an Ihre Daten angepasst ist
Wenn das nichtlineare Modell einen Prädiktor enthält, zeigt Minitab die Darstellung der Anpassungslinie an, in der die Beziehung zwischen der Antwortvariablen und den Prädiktordaten veranschaulicht wird. Die Darstellung enthält die Regressionslinie, die die Regressionsgleichung abbildet. Sie können auch angeben, dass in der Darstellung das 95%-Konfidenzintervall und das 95%-Prognoseintervall angezeigt werden sollen.
- Die Stichprobe enthält eine angemessene Anzahl von Beobachtungen über die gesamte Spannweite aller Prädiktorwerte.
- Das Modell ist an die Krümmung in den Daten angepasst. Um das beste Modell zu ermitteln, untersuchen Sie das Diagramm, den Standardfehler der Regression (S) sowie den Test auf fehlende Anpassung, wenn die Daten Replikationen enthalten.
- Suchen Sie nach Ausreißern, die einen starken Einfluss auf die Ergebnisse ausüben können. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen zum Erkennen von Ausreißern finden Sie unter Ungewöhnliche Beobachtungen.
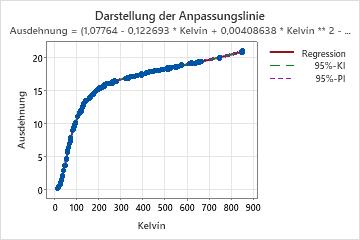
Schritt 2: Untersuchen der Beziehung zwischen den Prädiktoren und der Antwortvariablen
Verwenden Sie die Regressionsgleichung, um die Beziehung zwischen der Antwortvariablen und den Termen im Modell zu beschreiben. Die Regressionsgleichung ist eine algebraische Darstellung der Regressionslinie. Geben Sie den Wert jedes Prädiktors in die Gleichung ein, um den Mittelwert der Antwortvariablen zu berechnen. Im Gegensatz zur linearen Regression kann eine Gleichung für die nichtlineare Regression viele verschiedene Formen annehmen.
Bei nichtlinearen Gleichungen ist es häufig weniger intuitiv als bei linearen Gleichungen, die Effekte der einzelnen Prädiktoren auf die Antwortvariable zu ermitteln. Anders als bei den Parameterschätzwerten in linearen Modellen gibt es für Parameterschätzwerte in nichtlinearen Modellen keine einheitliche Interpretation. Die korrekte Interpretation für jeden Parameter hängt von der Modellfunktion und der Position des Parameters in der Formel ab. Wenn das nichtlineare Modell nur einen Prädiktor enthält, untersuchen Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen dem Prädiktor und der Antwortvariablen zu erkennen.
Wenn Sie ermitteln müssen, ob ein Parameterschätzwert statistisch signifikant ist, verwenden Sie die Konfidenzintervalle für die Parameter. Der Parameter ist statistisch signifikant, wenn die Spannweite nicht den Wert der Nullhypothese enthält. Minitab kann keine p-Werte für die Parameter in der nichtlinearen Regression berechnen. Bei der linearen Regression ist der Wert der Nullhypothese für jeden Parameter null (kein Effekt), und der p-Wert basiert auf diesem Wert. Bei der nichtlinearen Regression hängt der richtige Wert der Nullhypothese jedoch von der Modellfunktion und der Position des Parameters in der Formel ab.
Bei einigen Datensätzen, Modellfunktionen und Konfidenzintervallen ist möglicherweise nur eine oder gar keine Konfidenzgrenze vorhanden. Minitab zeigt das Fehlen von Ergebnissen durch ein Sternchen an. Wenn dem Konfidenzintervall eine der Grenzen fehlt, führt ein niedrigeres Konfidenzniveau möglicherweise zu einem beidseitigem Intervall.
Die Konvergenz gegen eine Lösung bedeutet nicht notwendigerweise eine optimale Anpassung des Modells oder eine minimale Summe der quadrierten Fehler (SSE). Aufgrund eines lokalen SSE-Minimums oder einer inkorrekten Modellfunktion kann der Algorithmus bei falschen Parameterwerten konvergieren. Daher ist es unerlässlich, die Parameterwerte, die Darstellung der Anpassungslinie und die Residuendiagramme zu untersuchen, um zu ermitteln, ob die Modellanpassung und die Parameterschätzwerte angemessen sind.
Gleichung
** 3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
Wichtigstes Ergebnis: Gleichung
In diesen Ergebnissen sind ein Prädiktor und sieben Parameterschätzwerte vorhanden. Die Antwortvariable ist „Ausdehnung“, während die Prädiktorvariable die Temperatur auf der Kelvin-Skala ist. Die umfangreiche Gleichung beschreibt die Beziehung zwischen der Antwortvariablen und den Prädiktoren. Der Effekt, den eine Erhöhung um 1 Grad Kelvin auf die Ausdehnung des Kupfers hat, hängt in hohem Maße vom der Ausgangstemperatur ab. Der Effekt der Temperaturänderungen auf die Kupferausdehnung kann nicht auf einfache Weise zusammengefasst werden. Untersuchen Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen dem Prädiktor und der Antwortvariablen zu erkennen.
Wenn Sie einen Wert für die Temperatur in Kelvin in die Gleichung einsetzen, ist das Ergebnis der angepasste Wert für die Kupferausdehnung.
Schritt 3: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken in der Tabelle „Zusammenfassung des Modells“ und in der Tabelle „Fehlende Anpassung“.
- S
-
Verwenden Sie S, um zu ermitteln, wie genau das Modell die Antwortvariable beschreibt.
S wird in der Maßeinheit der Antwortvariablen ausgedrückt und stellt den Abstand der Datenwerte von den angepassten Werten dar. Je niedriger der Wert von S, desto genauer beschreibt das Modell die Antwortvariable. Ein niedriger Wert von S allein bedeutet jedoch nicht zwangsläufig, dass das Modell die Modellannahmen erfüllt. Prüfen Sie die Annahmen anhand der Residuendiagramme.
- Fehlende Anpassung
-
Minitab zeigt die Tabelle „Fehlende Anpassung“ automatisch an, wenn die Daten Replikationen enthalten. Replikationen sind mehrere Beobachtungen mit identischen Prädiktorwerten. Wenn in den Daten keine Replikationen enthalten sind, kann der für diesen Test erforderliche reine Fehler nicht berechnet werden. Unterschiedliche Werte der Antwortvariablen für Replikationen stellen reine Fehler dar, da Unterschiede zwischen den beobachteten Werten der Antwortvariablen nur durch zufällige Streuung verursacht werden können.
Um zu bestimmen, ob das Modell die Beziehung zwischen der Antwortvariablen und den Prädiktoren richtig wiedergibt, vergleichen Sie den p-Wert für den Test auf fehlende Anpassung mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese für den Test auf fehlende Anpassung besagt, dass das Modell die Beziehung zwischen der Antwortvariablen und den Prädiktoren richtig darstellt. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass das Modell die Beziehung zwischen der Antwortvariablen und den Prädiktoren nicht richtig darstellt, während die Beziehung tatsächlich richtig angegeben wird, von 5 %.- p-Wert ≤ α: Die fehlende Anpassung ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass das Modell die Beziehung nicht richtig widerspiegelt. Zum Verbessern des Modells müssen Sie möglicherweise Terme hinzufügen oder die Daten transformieren.
- p-Wert > α: Die fehlende Anpassung ist statistisch nicht signifikant
-
Wenn der p-Wert größer als das Signifikanzniveau ist, wird mit dem Test keine fehlende Anpassung erkannt.
Fehlende Anpassung
| Quelle | DF | SS | MS | F | p |
|---|---|---|---|---|---|
| Fehler | 229 | 1,53244 | 0,0066919 | ||
| Fehlende Anpassung | 228 | 1,52583 | 0,0066922 | 1,01 | 0,679 |
| Reiner Fehler | 1 | 0,00661 | 0,0066125 |
Zusammenfassung
| Iterationen | 15 |
|---|---|
| Endgültige SSE | 1,53244 |
| DFE | 229 |
| MSE | 0,0066919 |
| S | 0,0818039 |
Wichtigste Ergebnisse: S, fehlende Anpassung
In diesen Ergebnissen gibt S an, dass die Standardabweichung der Distanz zwischen den Datenwerten und den angepassten Werten ungefähr 0,08 Einheiten beträgt. Der p-Wert für den Test auf fehlende Anpassung ist 0,679, und somit gibt es keine Anzeichen dafür, dass das Modell schlecht an die Daten angepasst ist.
Schritt 4: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.
Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Residuendiagramme für Nichtlineare Regression; klicken Sie dort auf den Namen des Residuendiagramms in der Liste am oberen Rand der Seite.
Diagramm der Residuen im Vergleich zu den Anpassungen
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |
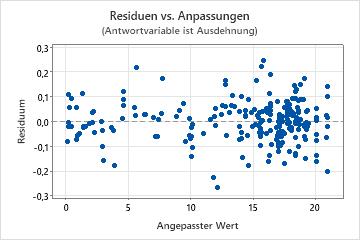
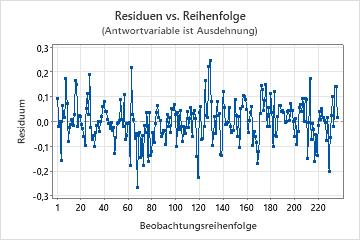
Diagramm der Residuen im Vergleich zur Reihenfolge
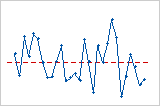
Trend
Shift
Zyklus
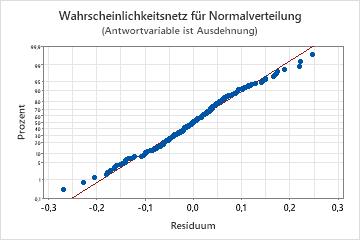
Wahrscheinlichkeitsnetz (Normal) für Residuen
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Keine Gerade | Nicht-Normalverteilung |
| Ein Punkt weit entfernt von der Linie | Ein Ausreißer |
| Unbeständige Steigung | Eine nicht identifizierte Variable |