Pareto-Diagramm
Minitab stellt ein Pareto-Diagramm der Effekte bereit, um die Ergebnisse aus der Koeffizienten- und der ANOVA-Tabelle zu veranschaulichen. Für die Terme im Modell können Sie anhand dieser Grafik die relative Größe der Effekte vergleichen und deren statistische Signifikanz beurteilen. Minitab zeichnet ein Pareto-Diagramm, wenn das Modell mindestens einen Freiheitsgrad für Fehler übrig lässt.
Der Schwellenwert für die statistische Signifikanz hängt vom Signifikanzniveau (angegeben durch α oder Alpha) ab. Wenn Sie keine schrittweise Auswahlmethode verwenden, ist das Signifikanzniveau gleich 1 minus dem Konfidenzniveau für die Analyse. Weitere Informationen zum Ändern des Konfidenzniveaus finden Sie unter Wählen Sie die Optionen für Regressionsmodell anpassen und Lineare Regression. Wenn Sie die Rückwärtsauswahl oder schrittweise Auswahl verwenden, entspricht das Signifikanzniveau dem Signifikanzniveau, bei dem Minitab einen Term aus dem Modell entfernt; dieses wird als Alpha für Ausschluss bezeichnet. Wenn Sie die Vorwärtsauswahl verwenden, entspricht das Signifikanzniveau dem Signifikanzniveau, bei dem Minitab dem Modell einen Term hinzufügt; dieses wird als Alpha für Aufnahme bezeichnet. Weitere Informationen zu Optionen für die schrittweisen Methoden finden Sie unter Führen Sie eine schrittweise Regression für Regressionsmodell anpassen und Lineare Regression durch.
Residuendiagramme
- Residuen für Diagramme
- Geben Sie den Typ der Residuen an, die in den Residuendiagrammen dargestellt werden sollen. Weitere Informationen finden Sie unter Welche Typen von Residuen sind in Minitab enthalten?.
- Regulär: Die regulären Rohresiduen werden dargestellt.
- Standardisiert: Die standardisierten Residuen werden dargestellt.
- Entfernt: Die studentisierten entfernten Residuen werden dargestellt.
- Residuendiagramme
- Verwenden Sie Residuendiagramme, um zu untersuchen, ob das Modell die Annahmen der Analyse erfüllt. Weitere Informationen finden Sie unter Residuendiagramme in Minitab.
- Einzelne Diagramme: Wählen Sie die Residuendiagramme aus, die angezeigt werden sollen.
- Histogramm der Residuen
- Ein Histogramm der Residuen wird angezeigt.
- Wahrscheinlichkeitsnetz (Normal) für Residuen
- Ein Wahrscheinlichkeitsnetz (Normal) für die Residuen wird angezeigt.
- Residuen vs. Anpassungen
- Ein Diagramm der Residuen im Vergleich zu den angepassten Werten wird angezeigt.
- Residuen vs. Reihenfolge
- Ein Diagramm der Residuen im Vergleich zur Reihenfolge der Daten wird angezeigt. Die Zeilennummer für jeden Datenpunkt wird auf der x-Achse abgetragen.
- Vier-in-eins: Alle vier Residuendiagramme werden zusammen in einer Grafik angezeigt.
- Einzelne Diagramme: Wählen Sie die Residuendiagramme aus, die angezeigt werden sollen.
- Residuen vs. Variablen
- Geben Sie eine oder mehrere Variablen ein, die im Vergleich zu den Residuen grafisch dargestellt werden sollen. Sie können die folgenden Typen von Variablen darstellen:
- Variablen, die bereits im aktuellen Modell enthalten sind, um nach einer Krümmung in den Residuen zu suchen.
- Wichtige Variablen, die im aktuellen Modell nicht enthalten sind, um festzustellen, ob sie in einer Beziehung zur Antwortvariablen stehen.
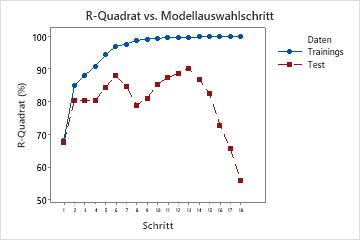
R-Quadrat vs. Modellauswahlschritt
Wenn Sie die Vorwärtsauswahl mit Validierung als schrittweises Verfahren verwenden, erzeugt Minitab ein Diagramm des R2 für den Trainingsdatensatz und entweder des R2 für den Test oder das R2 für K Faltungen mit schrittweiser Methode für jeden Schritt im Modellauswahlverfahren. Es hängt davon ab, ob Sie einen Testdatensatz oder die Kreuzvalidierung mit K Faltungen verwenden, ab das R2 für den Test oder das R2 für K Faltungen mit schrittweiser Methode angezeigt wird.
Interpretation
Verwenden Sie das Diagramm, um die verschiedenen R2-Werte in den einzelnen Schritten zu vergleichen. In der Regel zeigt das Modell eine gute Leistung, wenn beide R2-Werte groß sind. Minitab zeigt Regressionstatistiken für das Modell aus dem Schritt an, der entweder das R2 für den Test oder das R 2 für K Faltungen mit schrittweiser Methode maximiert. Das Diagramm zeigt, ob einfachere Modelle hinreichend passend sind, sodass auch sie gute potenzielle Modelle sein können.
Bei einer übermäßigen Anpassung eines Modells nimmt das R2 für den Test oder das R2 für K Faltungen mit schrittweiser Methode bei der Aufnahme von Termen in das Modell ab. Eine solche Abnahme erfolgt, während das entsprechende R2 für das Training oder das R2 für alle Daten weiterhin zunimmt. Ein Modell ist übermäßig angepasst, wenn Sie Terme für Effekte hinzufügen, die in der Grundgesamtheit nicht wichtig sind. Ein übermäßig angepasstes Modell eignet sich möglicherweise nicht, um Prognosen zur Grundgesamtheit vorzunehmen. Wenn ein Modell übermäßig angepasst ist, können Sie Modelle aus früheren Schritten untersuchen.
Im folgenden Diagramm wird als Beispiel das R2 für den Test angezeigt. Anfangs liegen beide R2-Werte nahe bei 70 %. In den ersten Schritte nehmen beide R2-Werte bei der Aufnahme von Termen in das Modell tendenziell zu. In Schritt 6 beträgt das R2 für den Test etwa 88 %. Der Maximalwert des R2 für den Test liegt in Schritt 14 vor, mit einem Wert von beinahe 90 %. Sie können überlegen, ob die Verbesserung der Anpassung die zusätzliche Komplexität durch die Aufnahme weiterer Terme in das Modell rechtfertigt.
Nach Schritt 14 nimmt das R2 weiterhin zu, das R2 für den Test hingegen nicht mehr. Die Abnahme des R2 für den Test nach Schritt 14 deutet auf eine übermäßige Anpassung des Modells hin.