In diesem Thema
Schritt 1: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Test R-Qd
- Je höher das R2, desto besser ist das Modell für Ihre Daten passend. R2 liegt immer zwischen 0% und 100%. Ausreißer haben eine größere Auswirkung auf das R2 als auf die MAD.
- Test Root Mean Squared Error (RMSE)
- Kleinere Werte weisen auf eine bessere Anpassung hin. Ausreißer wirken sich stärker auf RMSE aus als auf MAD.
- Mittlerer quadratischer Fehler (MSE)
- Kleinere Werte weisen auf eine bessere Anpassung hin. Ausreißer wirken sich stärker auf MSE aus als auf MAD.
- Mittlere absolute Abweichung des Tests (MAD)
- Kleinere Werte weisen auf eine bessere Anpassung hin. Die mittlere absolute Abweichung (MAD) drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann. Ausreißer haben eine geringere Auswirkung auf die MAD als auf das R2, die RMSE und den MSE.
Zusammenfassung des Modells
| Prädiktoren gesamt | 77 |
|---|---|
| Wichtige Prädiktoren | 10 |
| Maximale Anzahl von Basisfunktionen | 30 |
| Optimale Anzahl von Basisfunktionen | 13 |
| Statistiken | Trainings | Test |
|---|---|---|
| R-Quadrat | 89,61% | 87,61% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 25836,5197 | 27855,6550 |
| Mittlerer quadrierter Fehler (MSE) | 667525749,7185 | 775937512,8264 |
| Mittlere abs. Abweichung (MAD) | 17506,0038 | 17783,5549 |
Wichtigste Ergebnisse: Test R-Quadrat, Test Wurzel des mittleren quadrierten Fehlers (RMSE), Test Mittlerer quadrierter Fehler (MSE), Test Mittlere abs. Abweichung (MAD)
In diesen Ergebnissen beträgt der Test R-Quadrat etwa 88%. Der mittlere quadratische Fehler der Testwurzel beträgt etwa 27.856. Der mittlere quadratische Fehler des Tests beträgt etwa 775.937.513. Die mittlere absolute Abweichung des Tests beträgt etwa 17.784.
Schritt 2: Bestimmen, welche Variablen für das Modell am wichtigsten sind
Verwenden Sie das Diagramm zur relativen Variablenwichtigkeit, um zu sehen, welche Prädiktoren die wichtigsten Variablen für das Modell sind.
Wichtige Variablen befinden sich in mindestens 1 Basisfunktion im Modell. Die Variable mit dem höchsten Verbesserungswert wird als wichtigste Variable festgelegt, die übrigen Variablen folgen in entsprechender Reihenfolge. Bei der relativen Variablenwichtigkeit werden die Wichtigkeitswerte standardisiert, sodass sie leichter interpretiert werden können. Die relative Wichtigkeit ist als die prozentuale Verbesserung in Bezug auf den wichtigsten Prädiktor definiert.
Die Werte für die relative variable Wichtigkeit reichen von 0 % bis 100 %. Die wichtigste Variable hat immer eine relative Bedeutung von 100%. Wenn sich eine Variable nicht in einer Basisfunktion befindet, ist diese Variable nicht wichtig.
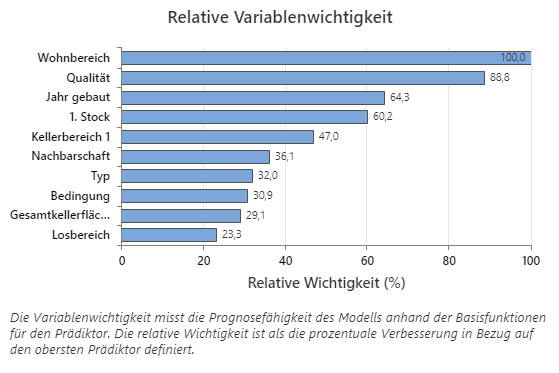
Wichtigstes Ergebnis: Relative Variablenwichtigkeit
- Qualität ist etwa 89% so wichtig wie Wohnbereich.
- Jahr gebaut ist etwa 64% so wichtig wie Wohnbereich.
- 1. Stock ist etwa 60% so wichtig wie Wohnbereich.
Obwohl diese Ergebnisse 10 Variablen mit positiver Wichtigkeit umfassen, liefert die relative Rangfolge Informationen darüber, wie viele Variablen für eine bestimmte Anwendung kontrolliert oder überwacht werden müssen. Ein steiler Abfall der relativen Wichtigkeit von einer Variablen zur nächsten Variablen können Ihnen die Entscheidung darüber erleichtern, welche Variablen zu kontrollieren oder zu überwachen sind. Zum Beispiel haben in diesen Daten die 2 wichtigsten Variablen Wichtigkeitswerte, die relativ nahe beieinander liegen, bevor die relative Wichtigkeit zur nächsten Variablen um über 20% abfällt. In ähnlicher Weise haben 2 Variablen ähnliche Wichtigkeitswerte über 60%. Sie können Variablen aus verschiedenen Gruppen entfernen und die Analyse wiederholen, um auszuwerten, wie Variablen in verschiedenen Gruppen die Prognosegenauigkeit in der Tabelle mit der Zusammenfassung des Modells beeinflussen.
Schritt 3: Untersuchen der Auswirkungen der Prädiktoren
Verwenden Sie die partiellen Abhängigkeitsdiagramme, die Basisfunktionen und die Koeffizienten in der Regressionsgleichung, um die Wirkung der Prädiktoren zu bestimmen. Die Auswirkungen der Prädiktoren erklären die Beziehung zwischen den Prädiktoren und der Antwortvariablen. Betrachten Sie alle Basisfunktionen für einen Prädiktor, um die Auswirkungen des Prädiktors auf die Antwortvariable zu verstehen.
Berücksichtigen Sie außerdem die Verwendung der wichtigen Prädiktoren und die Formen ihrer Beziehungen, wenn Sie andere Modelle erstellen. Wenn das MARS®-Regressionsmodell beispielsweise Interaktionen enthält, überlegen Sie, ob diese Interaktionen in ein Regressionsmodell der kleinsten Quadrate einbezogen werden sollen, um die Leistung der beiden Modelltypen zu vergleichen. In Anwendungen, in denen Sie die Prädiktoren steuern, bieten die Effekte eine natürliche Möglichkeit, die Einstellungen zu optimieren, um ein Ziel für die Antwortvariable zu erreichen.
In einem additiven Modell zeigen Ein-Prädiktor-, partielle Abhängigkeitsdiagramme, wie sich die wichtigen kontinuierlichen Prädiktoren auf die vorhergesagte Antwort auswirken. Das Diagramm der partiellen Abhängigkeit bei einem Prädiktor gibt an, wie sich die Antwort variablen Änderungen bei den Prädiktorebenen voraussichtlich ändert. Für MARS®-Regressionstammen die Werte im Diagramm aus den Basisfunktionen für den Prädiktor auf der x-Achse. Der Beitrag auf der y-Achse ist standardisiert, so dass der Mindestwert auf dem Diagramm 0 ist.
Wichtigstes Ergebnis: Diagramm der partiellen Abhängigkeit
Dieses Diagramm veranschaulicht, dass dies zunimmt, Verkaufspreis wenn die Wohnbereich minimale Quadratmeterzahl im Datensatz auf etwa 3.000 Quadratfuß steigt. Nach Wohnbereich dem Erreichen von 3.000 Quadratfuß wird der Beitrag Verkaufspreis bei etwa 152.000 US-Dollar flach.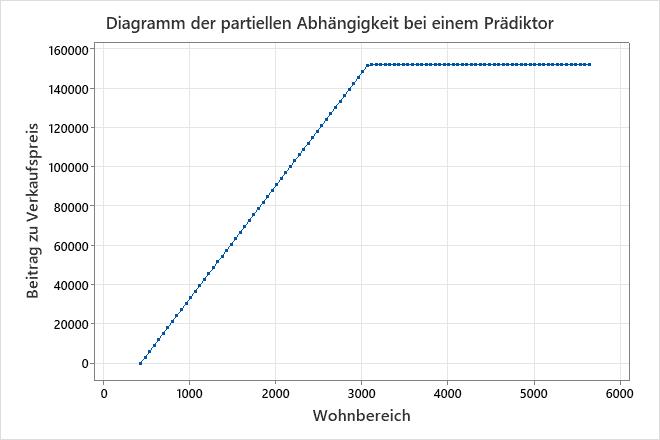
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Wichtigstes Ergebnis: Regressionsgleichung
In diesen Ergebnissen hat BF2 einen negativen Koeffizienten in der Regressionsgleichung. Der Koeffizient für die Basisfunktion ist −57,6167. Die Anordnung der Basisfunktion ist max(0, c − X). In dieser Anordnung nimmt der Wert der Basisfunktion ab, wenn der Prädiktor zunimmt. Die Kombination dieser Anordnung und des negativen Koeffizienten erzeugt eine positive Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen. Die Steigung von ist 57.6167 von Wohnbereich 438 bis 3,078.
Weitere Beispiele für allgemeine Basisfunktionen finden Sie unter Regressionsgleichung für MARS®-Regression.
