Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Suche nach dem besten Modelltyp
Ein Forscherteam erfasst und veröffentlicht detaillierte Informationen zu Faktoren, die Herzerkrankungen beeinflussen. Variablen sind Alter, Geschlecht, Cholesterinspiegel, Maximalpuls und viele weitere. Dieses Beispiel basiert auf einem öffentlichen Datensatz, der detaillierte Informationen über Herzerkrankungen liefert. Die Originaldaten stammen von der Website archive.ics.uci.edu.
Die Forscher wollen ein Modell finden, das möglichst genaue Vorhersagen trifft. Die Forscher verwenden Bestes Modell ermitteln (binäre Antwort) um die Vorhersageleistung von 4 Arten von Modellen zu vergleichen: binäre logistische Regression, TreeNet®, Random Forests® und CART®. Die Forscher planen, den Modelltyp mit der besten Vorhersageleistung weiter zu untersuchen.
- Öffnen Sie die Beispieldaten HerzKrankheitBinarBestesModell.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort die Spalte 'Herzkrankheiten' ein.
- Geben Sie in Stetige Prädiktoren, 'Rest Blutdruck', Cholesterin, 'Max Herzfrequenz' und ' Old Peak‚ Alter ein.
- Geben Kategoriale PrädiktorenSie Sexin , ' Brust Schmerz Typ', '', 'Fasten Blutzucker', 'Rest-EKG', '', Steigung,Übung Angina'Hauptblutgefäße' und Thal ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
In der Tabelle Modellauswahl wird die Leistung der verschiedenen Modelltypen verglichen. Das Modell "Random Forests"® hat den Minimalwert der durchschnittlichen –log-Wahrscheinlichkeit. Die folgenden Ergebnisse beziehen sich auf das beste Random Forests®-Modell.
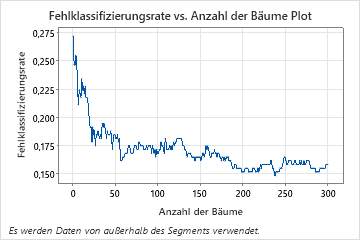
Das Diagramm der Fehlklassifizierungsrate vs. Anzahl der Bäume zeigt die gesamte Kurve über die Anzahl der aufgebauten Bäume. Die Fehlklassifizierungsrate liegt bei ca. 0,16.
Die Modellzusammenfassungstabelle zeigt, dass die durchschnittliche negative Logwahrscheinlichkeit etwa 0,39 beträgt.
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable ist „THAL“. Wenn der Beitrag der obersten Prädiktorvariablen, „THAL“, 100 % beträgt, hat die nächst wichtige Variable, „Hauptgefäße“, einen Beitrag von 98,9%. Das heißt, dass „Hauptgefäße“ in diesem Klassifikationsmodell 98,9% so wichtig wie „THAL“ ist.
Die Konfusionsmatrix zeigt, wie gut das Modell die Klassen korrekt trennt. In diesem Beispiel beträgt die Wahrscheinlichkeit, dass ein Ereignis richtig vorhergesagt wird, etwa 87 %. Die Wahrscheinlichkeit, dass ein Nicht-Ereignis richtig vorhergesagt wird, beträgt ca. 81 %.
Die Fehlklassifizierungsrate gibt an, ob das Modell neue Beobachtungen genau vorhersagen kann. Für die Vorhersage von Ereignissen beträgt der Fehler bei der Fehlklassifizierung außerhalb des Beutels ca. 13 %. Für die Vorhersage von Nichtereignissen beträgt der Fehlklassifizierungsfehler ca. 19 %. Insgesamt beträgt der Fehlklassifizierungsfehler für die Testdaten etwa 16 %.
Die Fläche unter der ROC-Kurve für das Random Forests®-Modell beträgt ungefähr 0,90 für die Out-of-Bag-Daten.
Methode
| Ein Modell der schrittweisen logistischen Regression mit linearen Termen und Termen 2. Ordnung anpassen. |
|---|
| 6 TreeNet®-Klassifikationsmodell(e) anpassen. |
| 3 Random Forests®-Klassifikationsmodell(e) mit Bootstrap-Stichprobenumfang gleich dem Trainingsdatenumfang von 303 anpassen. |
| Ein optimales CART®-Klassifikationsmodell anpassen. |
| Das Modell mit der maximalen Log-Likelihood aus der Kreuzvalidierung mit 5 Faltungen auswählen. |
| Gesamtzahl der Zeilen: 303 |
| Für Modell der logistischen Regression verwendete Zeilen: 303 |
| Für baumbasierte Modelle verwendete Zeilen: 303 |
Informationen zur binären Antwort
| Variable | Klasse | Anzahl | % |
|---|---|---|---|
| Herzkrankheiten | 1 (Ereignis) | 165 | 54,46 |
| 0 | 138 | 45,54 | |
| Alle | 303 | 100,00 |
| Bestes Modell innerhalb des Typs | Durchschnitt -Log-Likelihood | Fläche unter der ROC-Kurve | Fehlklassifizierungsrate |
|---|---|---|---|
| Random Forests®* | 0,3904 | 0,9048 | 0,1584 |
| TreeNet® | 0,3907 | 0,9032 | 0,1520 |
| Logistische Regression | 0,4671 | 0,9142 | 0,1518 |
| CART® | 1,8072 | 0,7991 | 0,2080 |
Hyperparameter für bestes Random Forests®-Modell
| Anzahl der Bootstrap-Stichproben | 300 |
|---|---|
| Stichprobenumfang | Entspricht Umfang der Trainingsdaten von 303 |
| Anzahl der für die Knotenteilung ausgewählten Prädiktoren | Quadratwurzel der Gesamtanzahl der Prädiktoren = 3 |
| Minimale interne Knotengröße | 8 |
Zusammenfassung des Modells
| Prädiktoren gesamt | 13 |
|---|---|
| Wichtige Prädiktoren | 13 |
| Statistiken | Außerhalb des Segments |
|---|---|
| Durchschnittliche -Log-Likelihood | 0,3904 |
| Fläche unter der ROC-Kurve | 0,9048 |
| 95%-KI | (0,8706; 0,9389) |
| Lift | 1,7758 |
| Fehlklassifizierungsrate | 0,1584 |
Konfusionsmatrix
| Prognostizierte Klasse (außerhalb des Segments) | ||||
|---|---|---|---|---|
| Tatsächliche Klasse | ||||
| Anzahl | 1 | 0 | % Richtig | |
| 1 (Ereignis) | 165 | 143 | 22 | 86,67 |
| 0 | 138 | 26 | 112 | 81,16 |
| Alle | 303 | 169 | 134 | 84,16 |
| Statistiken | Außerhalb des Segments (%) |
|---|---|
| Richtig-Positiv-Rate (Empfindlichkeit oder Trennschärfe) | 86,67 |
| Falsch-Positiv-Rate (Fehler 1. Art) | 18,84 |
| Falsch-Negativ-Rate (Fehler 2. Art) | 13,33 |
| Richtig-Negativ-Rate (Spezifität) | 81,16 |
Fehlklassifikation
| Tatsächliche Klasse | Außerhalb des Segments | ||
|---|---|---|---|
| Anzahl | Fehlklassifiziert | % Fehler | |
| 1 (Ereignis) | 165 | 22 | 13,33 |
| 0 | 138 | 26 | 18,84 |
| Alle | 303 | 48 | 15,84 |
Auswählen eines alternativen Modells
Die Forscher können sich Ergebnisse für andere Modelle aus der Suche nach dem besten Modell ansehen. Für ein TreeNet® -Modell können Sie aus einem Modell auswählen, das Teil der Suche war, oder Hyperparameter für ein anderes Modell angeben.
- Wählen Sie Alternatives Modell auswählen aus.
- Wählen Sie im Feld Modelltyp die Option TreeNet® aus.
- Wählen Sie in Vorhandenes Modell auswählen das dritte Modell aus, das den besten Wert für die minimale durchschnittliche Loglikelihood aufweist.
- Klicken Sie auf Anzeigen der Ergebnisse.
Interpretieren der Ergebnisse
Diese Analyse wächst 300 Bäume und die optimale Anzahl von Bäumen ist 46. Das Modell verwendet eine Lernrate von 0,1 und einen Teilstichprobenanteil von 0,5. Die maximale Anzahl von Endknoten pro Baum beträgt 6.
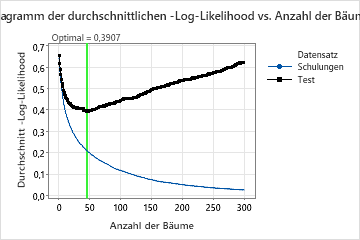
Das Diagramm der durchschnittlichen –Log-Likelihood vs. Anzahl der Bäume zeigt die gesamte Kurve über die Anzahl der aufgebauten Bäume. Der optimale Wert für die Testdaten ist 0,3907, wenn die Anzahl der Bäume 46 beträgt.
Zusammenfassung des Modells
| Prädiktoren gesamt | 13 |
|---|---|
| Wichtige Prädiktoren | 13 |
| Anzahl der aufgebauten Bäume | 300 |
| Optimale Anzahl von Bäumen | 46 |
| Statistiken | Trainings | Test |
|---|---|---|
| Durchschnittliche -Log-Likelihood | 0,2088 | 0,3907 |
| Fläche unter der ROC-Kurve | 0,9842 | 0,9032 |
| 95%-KI | (0,9721; 0,9964) | (0,8683; 0,9381) |
| Lift | 1,8364 | 1,7744 |
| Fehlklassifizierungsrate | 0,0726 | 0,1520 |
Wenn die Anzahl der Bäume 46 beträgt, gibt die Modellzusammenfassungstabelle an, dass die durchschnittliche negative Logwahrscheinlichkeit für die Trainingsdaten ungefähr 0,21 und für die Testdaten ungefähr 0,39 beträgt.
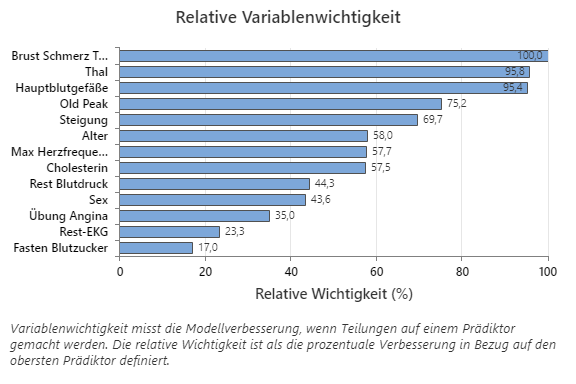
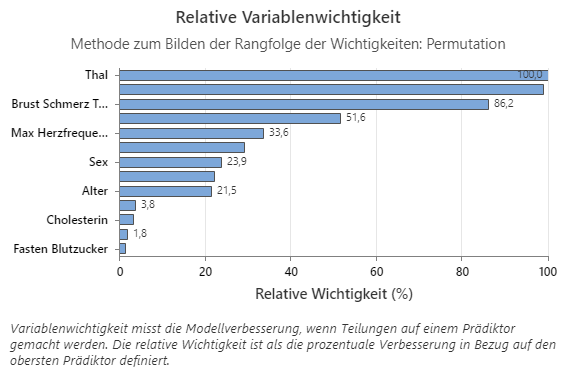
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable ist „Brustschmerztyp“. Wenn der Beitrag der obersten Prädiktorvariablen, des Brustschmerztyps, 100 % beträgt, dann hat die nächste wichtige Variable, Thal, einen Beitrag von 95,8 %. Das bedeutet, dass Thal in diesem Klassifikationsmodell zu 95,8 % so wichtig ist wie der Brustschmerztyp.
Konfusionsmatrix
| Prognostizierte Klasse (Trainings) | Prognostizierte Klasse (Test) | ||||||
|---|---|---|---|---|---|---|---|
| Tatsächliche Klasse | |||||||
| Anzahl | 1 | 0 | % Richtig | 1 | 0 | % Richtig | |
| 1 (Ereignis) | 165 | 156 | 9 | 94,55 | 147 | 18 | 89,09 |
| 0 | 138 | 13 | 125 | 90,58 | 28 | 110 | 79,71 |
| Alle | 303 | 169 | 134 | 92,74 | 175 | 128 | 84,82 |
| Statistiken | Trainings (%) | Test (%) |
|---|---|---|
| Richtig-Positiv-Rate (Empfindlichkeit oder Trennschärfe) | 94,55 | 89,09 |
| Falsch-Positiv-Rate (Fehler 1. Art) | 9,42 | 20,29 |
| Falsch-Negativ-Rate (Fehler 2. Art) | 5,45 | 10,91 |
| Richtig-Negativ-Rate (Spezifität) | 90,58 | 79,71 |
Die Konfusionsmatrix zeigt, wie gut das Modell die Klassen korrekt trennt. In diesem Beispiel beträgt die Wahrscheinlichkeit, dass ein Ereignis richtig vorhergesagt wird, etwa 89%. Die Wahrscheinlichkeit, dass ein Nicht-Ereignis richtig vorhergesagt wird, beträgt ca. 80%.
Fehlklassifikation
| Tatsächliche Klasse | Trainings | Test | |||
|---|---|---|---|---|---|
| Anzahl | Fehlklassifiziert | % Fehler | Fehlklassifiziert | % Fehler | |
| 1 (Ereignis) | 165 | 9 | 5,45 | 18 | 10,91 |
| 0 | 138 | 13 | 9,42 | 28 | 20,29 |
| Alle | 303 | 22 | 7,26 | 46 | 15,18 |
Die Fehlklassifizierungsrate hilft dabei, anzuzeigen, ob das Modell neue Beobachtungen genau vorhersagen kann. Für die Vorhersage von Ereignissen beträgt der Fehler bei der Fehlklassifizierung des Tests ca. 11 %. Für die Vorhersage von Nichtereignissen beträgt der Fehlklassifizierungsfehler ca. 20%. Insgesamt beträgt der Fehlklassifizierungsfehler für die Testdaten etwa 15%.
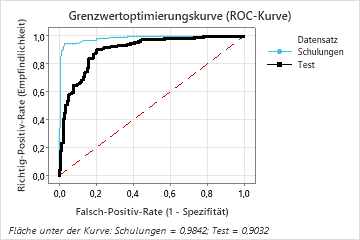
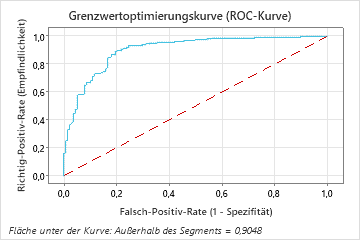
Die Fläche unter der ROC-Kurve bei einer Baumanzahl von 46 beträgt für die Trainingsdaten etwa 0,98 und für die Testdaten etwa 0,90.
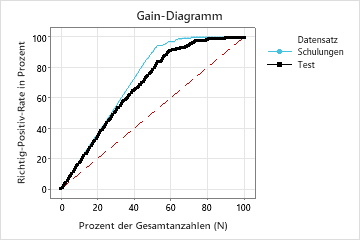
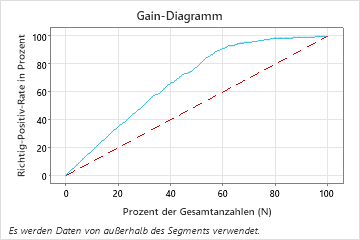
In diesem Beispiel zeigt das Gain-Diagramm einen starken Anstieg über die Referenzlinie und flacht dann ab. In diesem Fall machen ca. 60% der Daten ca. 90% der True Positives aus. Diese Differenz entspricht dem zusätzlichen Gain, der aus der Verwendung des Modells resultiert.
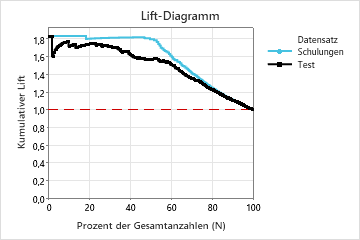
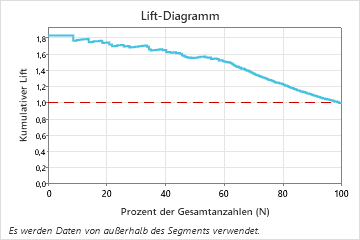
In diesem Beispiel zeigt das Lift-Diagramm einen starken Anstieg über der Referenzlinie, der nach etwa 50 % der Gesamtanzahl schneller abnimmt.
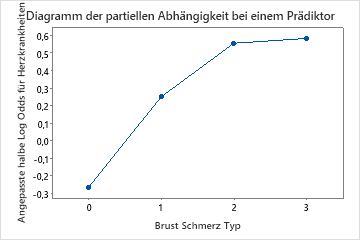
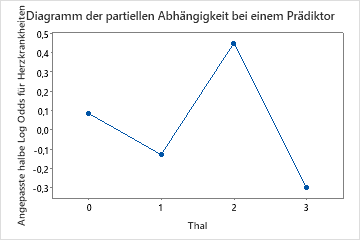

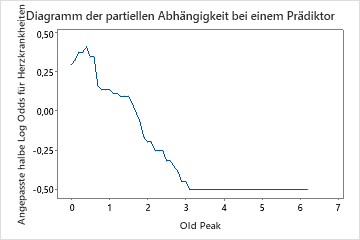
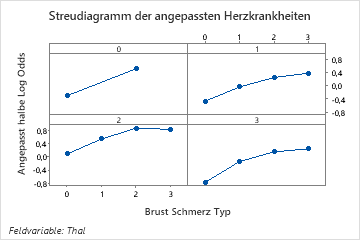
Verwenden Sie die partiellen Abhängigkeitsdiagramme, um einen Einblick in die Auswirkungen der wichtigen Variablen oder Variablenpaare auf die angepassten Antwortwerte zu erhalten. Die angepassten Antwortwerte liegen auf der 1/2 Log-Skala. Die Diagramme der partiellen Abhängigkeit zeigen, ob die Beziehung zwischen der Antwortvariablen und einer Variablen linear, monoton oder komplexer ist.
Im partiellen Abhängigkeitsdiagramm des Brustschmerztyps ist beispielsweise die Wahrscheinlichkeit von 1/2 log mit dem Wert 3 am höchsten. Auswählen oder Erstellen von Diagrammen für andere Variablen