Support für Minitab® 

Beispiel für Anpassen des Modells mit TreeNet®-Klassifikation

Weitere Informationen zu Minitab
Hinweis

Dieser Befehl ist mit dem Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.

Ein Forscherteam erfasst und veröffentlicht detaillierte Informationen zu Faktoren, die Herzerkrankungen beeinflussen. Variablen sind Alter, Geschlecht, Cholesterinspiegel, Maximalpuls und viele weitere. Dieses Beispiel basiert auf einem öffentlichen Datensatz, der detaillierte Informationen über Herzerkrankungen liefert. Die Originaldaten stammen von der Website archive.ics.uci.edu.

Nach der ersten Untersuchung mit CART® Klassifikation zur Identifizierung der wichtigen Prädiktoren verwenden die Forscher sowohl TreeNet®-Klassifikation als auch Random Forests®-Klassifikation, um intensivere Modelle aus demselben Datensatz zu erstellen. Die Forscher vergleichen die Tabelle mit der Zusammenfassung des Modells und das ROC-Diagramm aus den Ergebnissen, um zu bewerten, welches Modell ein besseres Prognoseergebnis liefert. Ergebnisse aus den anderen Analysen finden Sie unter Beispiel für CART® Klassifikation und Beispiel für Random Forests®-Klassifikation.

  1. Öffnen Sie die Beispieldaten Herz-Kreislauf-ErkrankungenBinar.MTW.
  2. Wählen Sie Predictive Analytics-Modul > TreeNet® Klassifikation > Modell anpassen aus.
  3. Wählen Sie in der Dropdown-Liste die Option Binäre Antwort aus.
  4. Geben Sie im Feld Antwort die Spalte Herzkrankheiten ein.
  5. Wählen Sie in Antwortereignis den Wert „1“ aus, um anzugeben, dass beim Patienten eine Herzerkrankung festgestellt wurde.
  6. Geben Sie im Feld Stetige Prädiktoren die Spalten Alter, Rest Blutdruck, Cholesterin, Max Herzfrequenz und Old Peak ein.
  7. Geben Sie im Feld Kategoriale Prädiktoren die Spalten Sex, Brust Schmerz Typ, Fasten Blutzucker, Rest-EKG, Übung Angina, Steigung, Hauptblutgefäße und Thal ein.
  8. Klicken Sie auf OK.

Interpretieren der Ergebnisse

Für diese Analyse baut Minitab 300 Bäume auf, und die optimale Anzahl von Bäumen beträgt 298. Da die optimale Anzahl von Bäumen nahe an der maximalen Anzahl von Bäumen liegt, die das Modell aufbaut, wiederholen die Forscher die Analyse mit mehr Bäumen.

TreeNet®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; Cholesterin; ...

Zusammenfassung des Modells Prädiktoren gesamt 13 Wichtige Prädiktoren 13 Anzahl der aufgebauten Bäume 300 Optimale Anzahl von Bäumen 298 Statistiken Schulungen Test Durchschnittliche -Log-Likelihood 0,2556 0,3881 Fläche unter der ROC-Kurve 0,9796 0,9089 95%-KI (0,9664; 0,9929) (0,8759; 0,9419) Lift 2,1799 2,1087 Fehlklassifizierungsrate 0,0891 0,1617

Beispiel mit 500 Bäumen

  1. Klicken Sie nach der Tabelle mit der Zusammenfassung des Modells auf Anpassen von Hyperparametern zum Identifizieren eines besseren Modells.
  2. Geben Sie im Feld Anzahl der Bäume den Wert 500 ein.
  3. Klicken Sie auf Anzeigen der Ergebnisse.

Interpretieren der Ergebnisse

Für diese Analyse wurden 500 Bäume aufgebaut, und die optimale Anzahl von Bäumen beträgt 351. Das beste Modell verwendet eine Trainingsrate von 0,01, verwendet eine Teilstichproben-Fraktion von 0,5 und 6 als maximale Anzahl von Endknoten.

TreeNet®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; Cholesterin; ...

Methode Kriterium für Auswahl der optimalen Anzahl von Bäumen Maximale Log-Likelihood Modellvalidierung Kreuzvalidierung mit 5 Faltungen Trainingsrate 0,01 Auswahlmethode für Teilstichprobe Vollständig zufällig Teilstichbruchfraktionschefin 0,5 Maximale Anzahl von Endknoten pro Baum 6 Minimale Endknotengröße 3 Anzahl der für die Knotenteilung ausgewählten Prädiktoren Gesamtanzahl der Prädiktoren = 13 Verwendete Zeilen 303
Informationen zur binären Antwort Variable Klasse Anzahl % Herzkrankheiten 1 (Ereignis) 139 45,87 0 164 54,13 Alle 303 100,00

TreeNet®-Klassifikation mit Hyperparameteranpassung: Herzkrankhei vs. Alter; Rest Blutdru; ...

Methode Kriterium für Auswahl der optimalen Anzahl von Bäumen Maximale Log-Likelihood Modellvalidierung Kreuzvalidierung mit 5 Faltungen Trainingsrate 0,001; 0,01; 0,1 Teilstichbruchfraktionschefin 0,5; 0,7 Maximale Anzahl von Endknoten pro Baum 6 Minimale Endknotengröße 3 Anzahl der für die Knotenteilung ausgewählten Prädiktoren Gesamtanzahl der Prädiktoren = 13 Verwendete Zeilen 303
Informationen zur binären Antwort Variable Klasse Anzahl % Herzkrankheiten 1 (Ereignis) 139 45,87 0 164 54,13 Alle 303 100,00
Optimierung der Hyperparameter Test Optimale Anzahl von Durchschnitt Fläche unter Modell Bäumen -Log-Likelihood der ROC-Kurve Fehlklassifizierungsrate 1 500 0,542902 0,902956 0,171749 2* 351 0,386536 0,908920 0,175027 3 33 0,396555 0,900782 0,161694 4 500 0,543292 0,894178 0,178142 5 374 0,389607 0,906620 0,165082 6 39 0,393382 0,901399 0,174973 Maximale Anzahl von Modell Trainingsrate Teilstichbruchfraktionschefin Endknoten 1 0,001 0,5 6 2* 0,010 0,5 6 3 0,100 0,5 6 4 0,001 0,7 6 5 0,010 0,7 6 6 0,100 0,7 6 * Das optimale Modell weist die minimale durchschnittliche –Log-Likelihood auf. Die Ausgabe für das optimale Modell folgt.

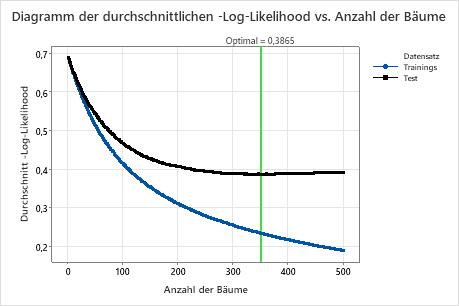
Das Diagramm der durchschnittlichen –Log-Likelihood vs. Anzahl der Bäume zeigt die gesamte Kurve über die Anzahl der aufgebauten Bäume. Der optimale Wert für die Testdaten ist 0,3865, wenn die Anzahl der Bäume 351 beträgt.

TreeNet®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; Cholesterin; ...

Zusammenfassung des Modells Prädiktoren gesamt 13 Wichtige Prädiktoren 13 Anzahl der aufgebauten Bäume 500 Optimale Anzahl von Bäumen 351 Statistiken Schulungen Test Durchschnittliche -Log-Likelihood 0,2341 0,3865 Fläche unter der ROC-Kurve 0,9825 0,9089 95%-KI (0,9706; 0,9945) (0,8757; 0,9421) Lift 2,1799 2,1087 Fehlklassifizierungsrate 0,0759 0,1750

Random Forests®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; ...

Zusammenfassung des Modells Prädiktoren gesamt 13 Wichtige Prädiktoren 13 Außerhalb des Statistiken Segments Durchschnittliche -Log-Likelihood 0,4004 Fläche unter der ROC-Kurve 0,9028 95%-KI (0,8693; 0,9363) Lift 2,1079 Fehlklassifizierungsrate 0,1848

Die Tabelle mit der Zusammenfassung des Modells zeigt, dass die durchschnittliche negative Log-Likelihood, wenn die Anzahl der Bäume 351 beträgt, für die Trainingsdaten ungefähr 0,23 und für die Testdaten ungefähr 0,39 beträgt. Diese Statistiken zeigen ein ähnliches Modell, wie es von Minitab Random Forests® erstellt wird. Auch die Fehlklassifizierungsraten sind ähnlich.

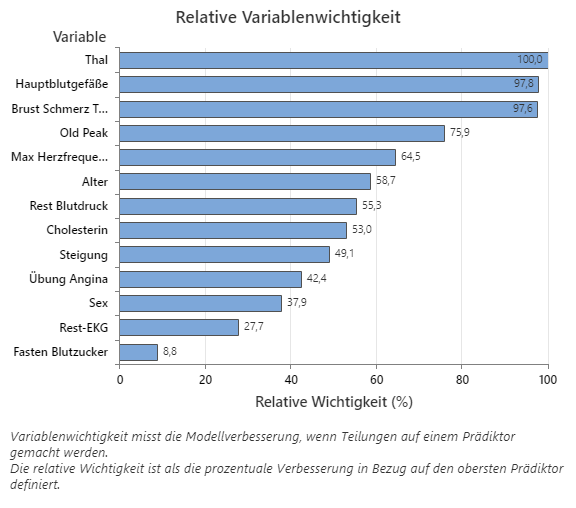
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable ist „THAL“. Wenn der Beitrag der obersten Prädiktorvariablen, „THAL“, 100 % beträgt, hat die nächst wichtige Variable, „Hauptgefäße“, einen Beitrag von 97,8 %. Das heißt, dass „Hauptgefäße“ in diesem Klassifikationsmodell 97,8 % so wichtig wie „THAL“ ist.

TreeNet®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; Cholesterin; ...

Konfusionsmatrix Prognostizierte Klasse Prognostizierte Klasse Tatsächliche (Schulungen) (Test) Klasse Anzahl 1 0 % Richtig 1 0 % Richtig 1 (Ereignis) 139 124 15 89,21 110 29 79,14 0 164 8 156 95,12 24 140 85,37 Alle 303 132 171 92,41 134 169 82,51 Die Zeile wird einer Ereignisklasse zugewiesen, wenn die Ereigniswahrscheinlichkeit für die Zeile 0,5 überschreitet.
Schulungen Statistiken (%) Test (%) Richtig-Positiv-Rate (Empfindlichkeit oder Trennschärfe) 89,21 79,14 Falsch-Positiv-Rate (Fehler 1. Art) 4,88 14,63 Falsch-Negativ-Rate (Fehler 2. Art) 10,79 20,86 Richtig-Negativ-Rate (Spezifität) 95,12 85,37

Die Konfusionsmatrix veranschaulicht, wie gut das Modell die Klassen korrekt trennt. In diesem Beispiel liegt die Wahrscheinlichkeit, dass ein Ereignis korrekt prognostiziert wird, bei 79,14 %. Die Wahrscheinlichkeit, dass ein Nicht-Ereignis korrekt prognostiziert wird, beträgt 85,37 %.

TreeNet®-Klassifikation: Herzkrankhei vs Alter; Rest Blutdru; Cholesterin; ...

Fehlklassifikation Tatsächliche Schulungen Test Klasse Anzahl Fehlklassifiziert % Fehler Fehlklassifiziert % Fehler 1 (Ereignis) 139 15 10,79 29 20,86 0 164 8 4,88 24 14,63 Alle 303 23 7,59 53 17,49 Die Zeile wird einer Ereignisklasse zugewiesen, wenn die Ereigniswahrscheinlichkeit für die Zeile 0,5 überschreitet.

Die Fehlklassifizierungsrate gibt an, ob das Modell neue Beobachtungen genau prognostizieren wird. Bei der Prognose von Ereignissen beträgt der Fehler bei der Fehlklassifikation im Test 20,86%. Bei der Prognose von Nicht-Ereignissen beträgt der Fehler bei der Fehlklassifikation 14,63% und insgesamt 17,49%.

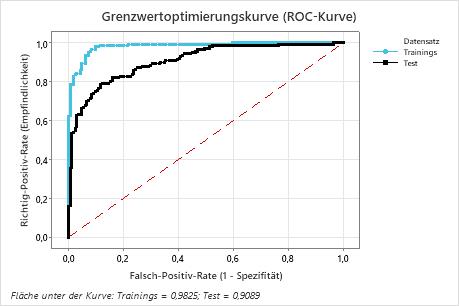
Die Fläche unter der ROC-Kurve bei einer Baumanzahl von 351 beträgt für die Trainingsdaten etwa 0,98 und für die Testdaten etwa 0,91. Dies zeigt eine gute Verbesserung gegenüber dem Modell aus CART® Klassifikation. Das Random Forests®-Klassifikation-Modell hat eine Test-AUROC von 0.9028, so dass diese 2 Methoden ähnliche Ergebnisse liefern.

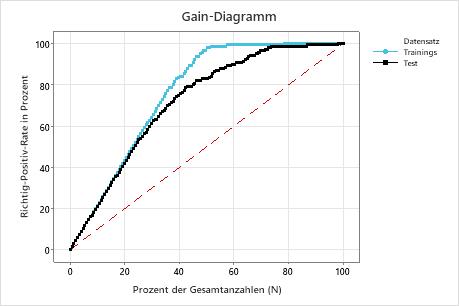
In diesem Beispiel zeigt das Gain-Diagramm einen starken Anstieg über die Referenzlinie und flacht dann ab. In diesem Fall sind rund 40 % der Daten für rund 80 % der Richtig-Positiven verantwortlich. Diese Differenz entspricht dem zusätzlichen Gain, der aus der Verwendung des Modells resultiert.

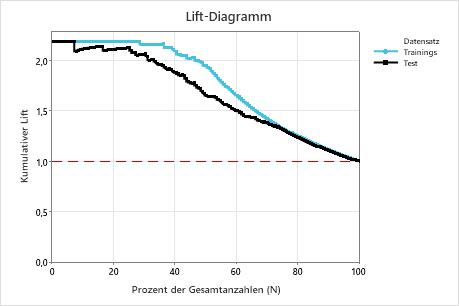
In diesem Beispiel zeigt das Lift-Diagramm einen starken Anstieg über die Referenzlinie und fällt dann ab.

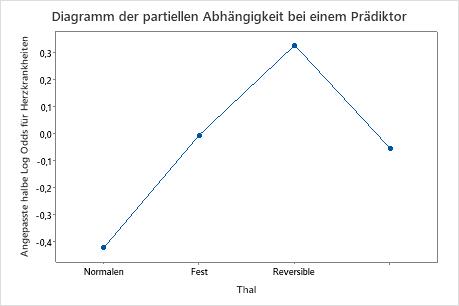
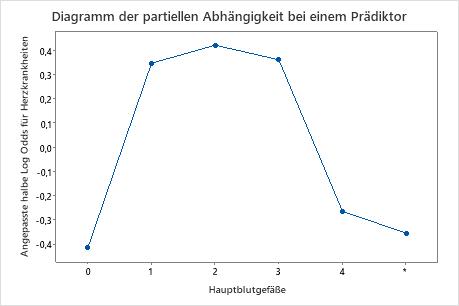
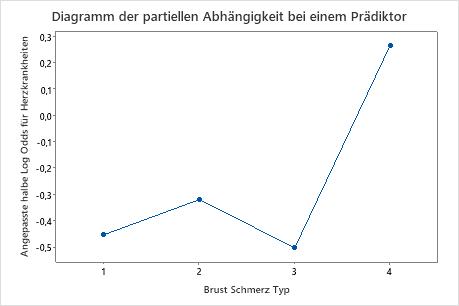
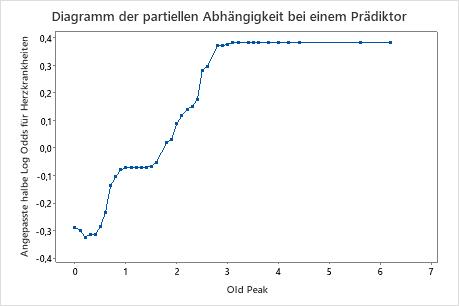
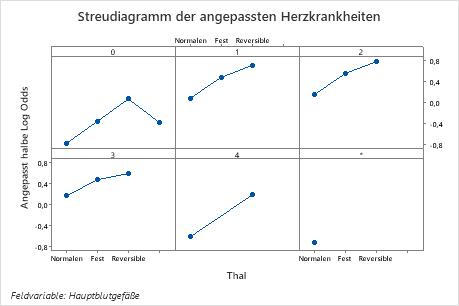
Verwenden Sie die Diagramme der partiellen Abhängigkeit, um zu erfahren, wie sich die wichtigen Variablen oder Variablenpaare auf den prognostizierten Wert der Antwortvariablen auswirken. Die Werte der Antwortvariablen auf der 1/2 Log-Skala sind die Prognosen aus dem Modell. Die Diagramme der partiellen Abhängigkeit zeigen, ob die Beziehung zwischen der Antwortvariablen und einer Variablen linear, monoton oder komplexer ist.

Im Diagramm der partiellen Abhängigkeit für den Brustschmerztyp variieren beispielsweise die 1/2 logarithmierten Chancen und steigen dann steil an. Wenn der Brustschmerztyp 4 ist, erhöht sich die 1/2 logarithmierte Chance des Auftretens einer Herzerkrankung von etwa –0,04 auf 0,03. Klicken Sie auf Auswählen weiterer Prädiktoren zur Darstellung, um Diagramme für andere Variablen zu erstellen.

Copyright © 2024 Minitab, LLC. All rights Reserved.