In diesem Thema
DF
Die Gesamt-Freiheitsgrade (DF) entsprechen der Menge an Informationen in Ihren Daten. In der Analyse werden diese Informationen verwendet, um die Werte von unbekannten Parametern der Grundgesamtheit zu schätzen. Die Gesamt-Freiheitsgrade werden durch die Anzahl der Beobachtungen in der Stichprobe bestimmt. Die DF für einen Term geben an, wie viele Informationen von dem betreffenden Term genutzt werden. Wenn Sie die Stichprobe vergrößern, stehen Ihnen mehr Informationen über die Grundgesamtheit und somit auch mehr Gesamt-Freiheitsgrade zur Verfügung. Durch Vergrößern der Anzahl von Termen im Modell werden mehr Informationen genutzt, wodurch die verfügbaren DF zum Schätzen der Streuung der Parameterschätzwerte abnehmen.
- DF für Krümmung
- Wenn ein Versuchsplan Zentralpunkte aufweist, ist ein Freiheitsgrad für den Test auf Krümmung vorgesehen. Wenn der Term für Zentralpunkte im Modell enthalten ist, stellt die Zeile für Krümmung einen Bestandteil des Modells dar. Wenn der Term für Zentralpunkte nicht im Modell enthalten ist, ist die Zeile für Krümmung Bestandteil des Fehlers, mit dem die Terme im Modell getestet werden.
- DF für Fehler
- Wenn zwei Bedingungen erfüllt sind, trennt Minitab die DF für Fehler ab, die nicht für die Krümmung vorgesehen sind. Die erste Bedingung ist, dass Terme vorhanden sein müssen, die für die Anpassung an die Daten verwendet werden können, jedoch im aktuellen Modell nicht enthalten sind. Dies ist beispielsweise der Fall, wenn der Versuchsplan Blöcke enthält, die Blöcke jedoch nicht im Modell enthalten sind. Der Zentralpunktterm ist immer für die Krümmung bestimmt, und daher zählt der Zentralpunktterm nicht als Term, der für die Anpassung an die Daten verwendet werden kann, aber nicht im aktuellen Modell enthalten ist.
Kor SS
Die korrigierte Summe der Quadrate ist ein Maß für die Streuung verschiedener Komponenten im Modell. Die Reihenfolge der Prädiktoren im Modell wirkt sich nicht auf die Berechnung der korrigierten Summe der Quadrate aus. In der Tabelle der Varianzanalyse verteilt Minitab die Summe der Quadrate auf verschiedene Komponenten, die die auf unterschiedliche Quellen zurückzuführende Streuung beschreiben.
- Kor SS für das Modell
- Die korrigierte Summe der Quadrate für das Modell entspricht der Differenz zwischen der Gesamtsumme der Quadrate und der Summe der Fehlerquadrate für das Modell im Vergleich mit einem Modell, in dem lediglich der Mittelwert der Antwortvariablen verwendet wird. Es handelt sich um die Summe aller sequenziellen Summen der Quadrate für die Terme im Modell.
- Kor SS für Gruppen von Termen
- Die korrigierte Summe der Quadrate für eine Gruppe von Termen entspricht der Summe der sequenziellen Summen der Quadrate für alle Terme in der betreffenden Gruppe. Sie ist ein Maß der Streuung in den Daten der Antwortvariablen, die durch die Gruppe von Termen erklärt wird.
- Kor SS für einen Term
- Die korrigierte Summe der Quadrate für einen Term ist die Zunahme der Summe der Quadrate für das Modell im Vergleich mit einem Modell, das lediglich die anderen Terme enthält. Dieser Wert ist ein Maß für den Anteil der Streuung in den Daten der Antwortvariablen, die durch die einzelnen Terme im Modell erklärt wird.
- Kor SS für Fehler
- Die korrigierte Summe der Fehlerquadrate ist die Summe der quadrierten Residuen. Dieser Wert ist ein Maß für die Streuung in den Daten, die durch die Prädiktoren nicht erklärt wird.
- Kor SS für Krümmung
- Die korrigierte Summe der Quadrate für die Krümmung kann Teil der Summe der Quadrate für das Modell oder Teil der Summe der Fehlerquadrate sein. Dieser Wert ist ein Maß für den Anteil der Streuung in den Daten der Antwortvariablen, die durch den Zentralpunktterm erklärt wird. Diese Streuung stellt den kombinierten Effekt eines oder mehrerer quadratischer Terme dar.
- Kor SS für reine Fehler
- Die korrigierte Summe der Quadrate für reine Fehler ist Teil der Summe der Fehlerquadrate. Die Summe der Quadrate für reine Fehler ist vorhanden, wenn Freiheitsgrade für reine Fehler vorliegen. Weitere Informationen finden Sie im Abschnitt zu Freiheitsgraden (DF). Dieser Wert ist ein Maß für die Streuung in den Daten für Beobachtungen, die dieselben Werte für die Faktoren, Blöcke und Kovariaten aufweisen.
- Kor SS Gesamt
- Die korrigierte Gesamtsumme der Quadrate ist die Summe der Summe der Quadrate für das Modell und der Summe der Fehlerquadrate. Dieser Wert ist ein Maß für die Gesamtstreuung in den Daten.
Interpretation
Minitab verwendet die korrigierten Summen der Quadrate, um die p-Werte in der ANOVA-Tabelle zu berechnen. Zudem verwendet Minitab die Summen der Quadrate, um das R2 zu berechnen. Im Allgemeinen interpretieren Sie die p-Werte sowie das R2 und nicht die Summen der Quadrate.
Kor MS
Mit dem korrigierten Mittel der Quadrate wird angegeben, wie viel der Streuung von einem Term oder einem Modell erklärt wird; hierbei wird angenommen, dass alle übrigen Terme im Modell enthalten sind, jedoch wird ihre Reihenfolge im Modell außer Acht gelassen. Im Unterschied zur korrigierten Summe der Quadrate werden beim korrigierten Mittel der Quadrate die Freiheitsgrade berücksichtigt.
Der korrigierte mittlere quadrierte Fehler (auch als MSE oder s2 bezeichnet) ist die Varianz um die angepassten Werte.
Interpretation
Minitab verwendet die korrigierten Mittel der Quadrate, um die p-Werte in der ANOVA-Tabelle zu berechnen. Außerdem verwendet Minitab das korrigierte Mittel der Quadrate, um das korrigierte R2 zu berechnen. Im Allgemeinen interpretieren Sie die p-Werte und das korrigierte R2 und nicht das korrigierte Mittel der Quadrate.
Seq SS
Die sequenzielle Summe der Quadrate ist ein Maß für die Streuung verschiedener Komponenten im Modell. Im Unterschied zur korrigierten Summe der Quadrate hängt die sequenzielle Summe der Quadrate von der Reihenfolge ab, in der die Terme in das Modell aufgenommen wurden. In der Tabelle der Varianzanalyse verteilt Minitab die sequenzielle Summe der Quadrate auf verschiedene Komponenten, die die auf unterschiedliche Quellen zurückzuführende Streuung beschreiben.
- Seq SS für das Modell
- Die sequenzielle Summe der Quadrate für das Modell entspricht der Differenz zwischen der Gesamtsumme der Quadrate und der Summe der Fehlerquadrate. Es handelt sich um die Summe aller Summen der Quadrate für die Terme im Modell.
- Seq SS für Gruppen von Termen
- Die sequenzielle Summe der Quadrate für eine Gruppe von Termen im Modell entspricht der Summe der Summen der Quadrate für alle Terme in der betreffenden Gruppe. Sie ist ein Maß der Streuung in den Daten der Antwortvariablen, die durch die Gruppe von Termen erklärt wird.
- Seq SS für einen Term
- Die sequenzielle Summe der Quadrate für einen Term ist die Zunahme der Summe der Quadrate für das Modell im Vergleich mit einem Modell, das lediglich die in der ANOVA-Tabelle darüber aufgeführten Terme enthält. Sie ist ein Maß für die Zunahme der Summe der Quadrate für das Modell, wenn der betreffende Term zu einem Modell mit den darüber aufgeführten Termen hinzugefügt wird.
- Seq SS für Fehler
- Die sequenzielle Summe der Fehlerquadrate ist die Summe der quadrierten Residuen. Dieser Wert ist ein Maß für die Streuung in den Daten, die durch die Prädiktoren nicht erklärt wird.
- Seq SS für Krümmung
- Die sequenzielle Summe der Quadrate für die Krümmung kann Teil der Summe der Quadrate für das Modell oder Teil der Summe der Fehlerquadrate sein. Dieser Wert ist ein Maß für den Anteil der Streuung in den Daten der Antwortvariablen, die durch den Zentralpunktterm erklärt wird. Diese Streuung stellt den kombinierten Effekt eines oder mehrerer quadratischer Terme dar.
- Seq SS für reine Fehler
- Die sequenzielle Summe der Quadrate für reine Fehler ist Teil der Summe der Fehlerquadrate. Die Summe der Quadrate für reine Fehler ist vorhanden, wenn Freiheitsgrade für reine Fehler vorliegen. Weitere Informationen finden Sie im Abschnitt zu Freiheitsgraden (DF). Dieser Wert ist ein Maß für die Streuung in den Daten für Beobachtungen, die dieselben Werte für die Faktoren, Blöcke und Kovariaten aufweisen.
- Seq SS Gesamt
- Die sequenzielle Gesamtsumme der Quadrate ist die Summe der Summen der Quadrate für das Modell und der Summen der Fehlerquadrate. Dieser Wert ist ein Maß für die Gesamtstreuung in den Daten.
Interpretation
Minitab verwendet die sequenziellen Summen der Quadrate beim Analysieren eines Versuchsplans nicht, um p-Werte zu berechnen, Sie können die sequenziellen Summen der Quadrate jedoch beim Ausführen der Befehle Regressionsmodell anpassen und Allgemeines lineares Modell anpassen verwenden. Im Allgemeinen interpretieren Sie die p-Werte und das R2 auf der Grundlage der korrigierten Summe der Quadrate.
Beitrag
Mit dem Beitrag wird der prozentuale Beitrag jeder Quelle in der Tabelle der Varianzanalyse zur sequenziellen Gesamtsumme der Quadrate (Seq SS) angezeigt.
Interpretation
Höhere Prozentsätze zeigen an, dass die Quelle einen größeren Anteil zur Streuung der Antwortvariablen beiträgt.
F-Wert
Für jeden Test in der Tabelle der Varianzanalyse wird ein F-Wert angezeigt.
- F-Wert für das Modell
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine Assoziation zwischen einem Term im Modell und der Antwortvariablen besteht; dies schließt Kovariaten, Blöcke, Faktorterme und Krümmung ein.
- F-Wert für Kovariaten als Gruppe
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine simultane Assoziation zwischen mehreren Kovariaten und der Antwortvariablen besteht.
- F-Wert für einzelne Kovariaten
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine Assoziation zwischen einer einzelnen Kovariaten und der Antwortvariablen besteht.
- F-Wert für Blöcke
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine Assoziation zwischen den unterschiedlichen Bedingungen der Blöcke und der Antwortvariablen besteht.
- F-Wert für Typen von Faktortermen
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine Assoziation zwischen einer Gruppe von Termen und der Antwortvariablen besteht. Beispiele für Gruppen von Termen sind lineare Effekte und Zwei-Faktor-Wechselwirkungen.
- F-Wert für einzelne Terme
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob eine Assoziation zwischen dem Term und der Antwortvariablen besteht.
- F-Wert für Krümmung
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob ein oder mehrere Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen stehen.
- F-Wert für den Test auf fehlende Anpassung
- Der F-Wert ist die Teststatistik, anhand derer bestimmt wird, ob im Modell Terme fehlen, die die Faktoren aus dem Experiment enthalten. Wenn Blöcke oder Kovariaten in einem schrittweisen Verfahren aus dem Modell ausgeschlossen werden, sind diese Terme auch im Test auf fehlende Anpassung enthalten.
Interpretation
Minitab verwendet den F-Wert zum Berechnen des p-Werts, anhand dessen Sie eine Entscheidung über die statistische Signifikanz des Tests treffen können. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft. Ein hinreichend großer F-Wert gibt eine statistische Signifikanz an.
Wenn Sie mit dem F-Wert feststellen möchten, ob die Nullhypothese zurückzuweisen ist, vergleichen Sie den F-Wert mit dem kritischen Wert. Sie können den kritischen Wert in Minitab berechnen oder diesen einer in den meisten Fachbüchern vorhandenen Tabelle für die F-Verteilung entnehmen. Weitere Informationen zum Berechnen des kritischen Werts mit Hilfe von Minitab finden Sie unter Verwenden der inversen kumulativen Verteilungsfunktion (ICDF); klicken Sie dort auf „Verwenden der ICDF zum Berechnen von kritischen Werten“.
p-Wert – Modell
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Um zu bestimmen, ob das Modell die Streuung in der Antwortvariablen erklärt, vergleichen Sie den p-Wert für das Modell mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese für das Modell besagt, dass das Modell die Streuung in der Antwortvariablen nicht erklärt. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass das Modell die Streuung in der Antwortvariablen erklärt, während dies tatsächlich nicht der Fall ist, von 5 %.
- p-Wert ≤ α: Das Modell erklärt die Streuung in der Antwortvariablen
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass das Modell die Streuung in der Antwortvariablen erklärt.
- p-Wert > α: Es liegen keine ausreichenden Anzeichen dafür vor, dass das Modell die Streuung in der Antwortvariablen erklärt
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass das Modell die Streuung in der Antwortvariablen erklärt. Es empfiehlt sich möglicherweise, ein neues Modell anzupassen.
p-Wert – Kovariaten
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
In einem Versuchsplan werden mit Kovariaten die Variablen erklärt, die zwar gemessen, jedoch nur schwer kontrolliert werden können. Die Mitglieder eines Qualitätssicherungsteams in einem Krankenhausverbund entwerfen beispielsweise einen Versuchsplan, mit dem die Aufenthaltsdauer von Patienten untersucht werden soll, die wegen einer Knieprothesen-Operation aufgenommen wurden. Für den Versuchsplan können die Teammitglieder Faktoren wie das Format der präoperativen Anweisungen kontrollieren. Um eine Verzerrung auszuschließen, erfasst das Team Daten zu Kovariaten, die nicht kontrolliert werden können, z. B. das Alter des Patienten.
Interpretation
Um zu bestimmen, ob die Assoziation zwischen der Antwortvariablen und einer Kovariaten statistisch signifikant ist, vergleichen Sie den p-Wert für die Kovariate mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass der Koeffizient für die Kovariate gleich null ist, was darauf hinweist, dass keine Assoziation zwischen der Kovariaten und der Antwortvariablen besteht.
In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 % für die Schlussfolgerung an, dass sich die Antwortvariable durch unterschiedliche Bedingungen bei den einzelnen Durchläufen ändert, während dies tatsächlich nicht der Fall ist.
Berücksichtigen Sie die Varianzinflationsfaktoren (VIF), wenn Sie die statistische Signifikanz von Termen für ein Modell mit Kovariaten beurteilen.
- p-Wert ≤ α: Die Assoziation ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und der Kovariaten besteht.
- p-Wert > α: Die Assoziation ist statistisch nicht signifikant
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass die Assoziation zwischen der Antwortvariablen und der Kovariaten statistisch signifikant ist. Es empfiehlt sich möglicherweise, ein Modell ohne die Kovariate anzupassen.
Hinweis
In den meisten faktoriellen Versuchsplänen sind sämtliche VIF-Werte gleich 1 – ein Umstand, der das Bestimmen der statistischen Signifikanz erleichtert. Die Interpretation der statistischen Signifikanz wird jedoch durch das Einbinden von Kovariaten in das Modell und das Auftreten misslungener Durchläufe während der Datenerfassung erschwert, da dies zwei gängige Gründe dafür sind, dass die VIF-Werte ansteigen. Die VIF-Werte werden in der Koeffiziententabelle aufgeführt. Weitere Informationen finden Sie unter Koeffiziententabelle für Faktoriellen Versuchsplan analysieren; klicken Sie dort auf „VIF“.
p-Wert – Blöcke
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Blöcke erklären die Differenzen, die zwischen Durchläufen auftreten können, die unter unterschiedlichen Bedingungen ausgeführt werden. Ein Techniker entwickelt beispielsweise einen Versuchsplan, in dem ein Schweißprozess untersucht wird, und dabei kann er nicht alle Daten am gleichen Tag erfassen. Die Schweißqualität wird durch verschiedene Variablen beeinflusst, die sich von Tag zu Tag ändern und außerhalb der Kontrolle des Technikers liegen, z. B. durch die relative Luftfeuchtigkeit. Um diese nicht kontrollierbaren Variablen zu berücksichtigen, gruppiert der Techniker die täglich ausgeführten Durchläufe in separaten Blöcken. Die Blöcke erklären die Streuung durch die nicht kontrollierbaren Variablen, so dass diese Effekte nicht mit den Effekten der Faktoren verwechselt werden, die untersucht werden sollen. Weitere Informationen dazu, wie Minitab Durchläufe zu Blöcken zuordnet, finden Sie unter Was ist ein Block?.
Interpretation
Um zu bestimmen, ob die Antwortvariable durch unterschiedliche Bedingungen zwischen den Durchläufen geändert wird, vergleichen Sie den p-Wert für die Blöcke mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass die Antwortvariable durch unterschiedliche Bedingungen nicht geändert wird.
In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 % für die Schlussfolgerung an, dass sich die Antwortvariable durch unterschiedliche Bedingungen bei den einzelnen Durchläufen ändert, während dies tatsächlich nicht der Fall ist.
- p-Wert ≤ α: Die Antwortvariable wird durch die unterschiedlichen Bedingungen geändert
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass die Antwortvariable durch die unterschiedlichen Bedingungen geändert wird.
- p-Wert > α: Es liegen keine ausreichenden Anzeichen dafür vor, dass die unterschiedlichen Bedingungen eine Änderung der Antwortvariablen bewirken
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass die Antwortvariable durch unterschiedliche Bedingungen geändert wird. Es empfiehlt sich möglicherweise, ein Modell ohne Blöcke anzupassen.
p-Wert – Faktoren, Wechselwirkungen und Gruppen von Termen
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
- Wenn eine Kovariate signifikant ist, können Sie schlussfolgern, dass der Koeffizient für die Kovariate ungleich null ist.
- Wenn ein kategorialer Faktor signifikant ist, können Sie schlussfolgern, dass nicht alle Mittelwerte der Faktorstufen gleich sind.
- Wenn ein Wechselwirkungsterm signifikant ist, können Sie schlussfolgern, dass die Beziehung zwischen einem Faktor und der Antwortvariablen von den anderen Faktoren im Term abhängt.
Testen von Gruppen von Termen
Wenn eine Gruppe von Termen statistisch signifikant ist, können Sie schlussfolgern, dass mindestens einer der Terme in der Gruppe einen Effekt auf die Antwortvariable hat. Wenn Sie anhand der statistischen Signifikanz entscheiden, welche Terme im Modell beibehalten werden sollen, entfernen Sie in der Regel keine ganzen Gruppen von Termen gleichzeitig. Die statistische Signifikanz von einzelnen Termen kann sich auf der Grundlage der im Modell enthaltenen Terme ändern.
Varianzanalyse
| Quelle | DF | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Modell | 10 | 447,766 | 44,777 | 17,61 | 0,003 |
| Linear | 4 | 428,937 | 107,234 | 42,18 | 0,000 |
| Material | 1 | 181,151 | 181,151 | 71,25 | 0,000 |
| EinsprDruck | 1 | 112,648 | 112,648 | 44,31 | 0,001 |
| EinsprTemp | 1 | 73,725 | 73,725 | 29,00 | 0,003 |
| AbkühlTemp | 1 | 61,412 | 61,412 | 24,15 | 0,004 |
| 2-Faktor-Wechselwirkungen | 6 | 18,828 | 3,138 | 1,23 | 0,418 |
| Material*EinsprDruck | 1 | 0,342 | 0,342 | 0,13 | 0,729 |
| Material*EinsprTemp | 1 | 0,778 | 0,778 | 0,31 | 0,604 |
| Material*AbkühlTemp | 1 | 4,565 | 4,565 | 1,80 | 0,238 |
| EinsprDruck*EinsprTemp | 1 | 0,002 | 0,002 | 0,00 | 0,978 |
| EinsprDruck*AbkühlTemp | 1 | 0,039 | 0,039 | 0,02 | 0,906 |
| EinsprTemp*AbkühlTemp | 1 | 13,101 | 13,101 | 5,15 | 0,072 |
| Fehler | 5 | 12,712 | 2,542 | ||
| Gesamt | 15 | 460,478 |
In diesem Modell ist der Test auf Zwei-Faktor-Wechselwirkungen auf einem Niveau von 0,05 statistisch nicht signifikant. Außerdem sind die Tests für alle Zwei-Faktor-Wechselwirkungen statistisch nicht signifikant.
Varianzanalyse
| Quelle | DF | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Modell | 5 | 442,04 | 88,408 | 47,95 | 0,000 |
| Linear | 4 | 428,94 | 107,234 | 58,16 | 0,000 |
| Material | 1 | 181,15 | 181,151 | 98,24 | 0,000 |
| EinsprDruck | 1 | 112,65 | 112,648 | 61,09 | 0,000 |
| EinsprTemp | 1 | 73,73 | 73,725 | 39,98 | 0,000 |
| AbkühlTemp | 1 | 61,41 | 61,412 | 33,31 | 0,000 |
| 2-Faktor-Wechselwirkungen | 1 | 13,10 | 13,101 | 7,11 | 0,024 |
| EinsprTemp*AbkühlTemp | 1 | 13,10 | 13,101 | 7,11 | 0,024 |
| Fehler | 10 | 18,44 | 1,844 | ||
| Gesamt | 15 | 460,48 |
Wenn Sie das Modell ausgehend von der Zwei-Faktor-Wechselwirkung mit dem höchsten p-Wert jeweils um einen einzelnen Term reduzieren, ist die letzte Zwei-Faktor-Wechselwirkung auf dem Niveau 0,05 statistisch signifikant.
p-Wert – Krümmung
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Minitab führt einen Test auf Krümmung durch, wenn der Versuchsplan Zentralpunkte aufweist. Im Test wird der angepasste Mittelpunkt der Antwortvariablen bei den Zentralpunkten im Vergleich mit dem Mittelpunkt untersucht, der zu erwarten wäre, wenn die Beziehungen zwischen den Modelltermen und der Antwortvariablen linear wäre. Verwenden Sie Faktordiagramme, um die Krümmung grafisch zu veranschaulichen.
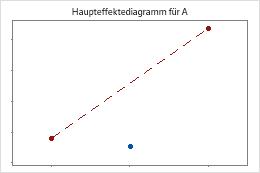
Die Zentralpunkte liegen weit entfernt von der Linie, die die Mittelwerte der Eckpunkte verbindet, was auf eine gekrümmte Beziehung hinweist. Verwenden Sie den p-Wert, um zu prüfen, ob die Krümmung statistisch signifikant ist.
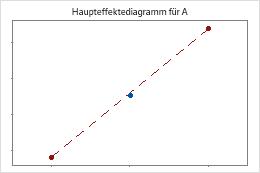
Die Zentralpunkte liegen dicht an der Linie, die die Mittelwerte der Eckpunkte verbindet. Die Krümmung ist wahrscheinlich statistisch nicht signifikant.
Interpretation
Um zu bestimmen, ob sich mindestens einer der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen befindet, vergleichen Sie den p-Wert für Krümmung mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass alle Beziehungen zwischen den Faktoren und der Antwortvariablen linear sind.
In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 % für die Schlussfolgerung an, dass sich die Antwortvariable durch unterschiedliche Bedingungen bei den einzelnen Durchläufen ändert, während dies tatsächlich nicht der Fall ist.
- p-Wert ≤ α: Mindestens ein Faktor befindet sich in einer gekrümmten Beziehung mit der Antwortvariablen
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, schlussfolgern Sie, dass sich mindestens einer der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen befindet. Es empfiehlt sich, dem Versuchsplan Sternpunkte hinzuzufügen, um auf diese Weise die Krümmung zu modellieren.
- p-Wert > α: Es liegen keine ausreichenden Anzeichen für die Schlussfolgerung vor, dass einer der Faktoren über eine gekrümmte Beziehung mit der Antwortvariablen verfügt
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass einer oder mehrere der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen steht. Wenn die Krümmung Teil des Modells ist, empfiehlt es sich möglicherweise, das Modell ohne einen Term für Zentralpunkte neu anzupassen, so dass die Krümmung Teil des Fehlers ist.
Hinweis
Wenn die Krümmung statistisch nicht signifikant ist, entfernen Sie im Allgemeinen den Zentralpunktterm. Wenn Sie die Zentralpunkte im Modell belassen, geht Minitab davon aus, dass das Modell eine Krümmung aufweist, die für den faktoriellen Versuchsplan nicht passend ist. Aufgrund der unzureichenden Anpassung stehen die Optionen Konturdiagramm, Wirkungsflächendiagramm und Überlagertes Konturdiagramm nicht zur Verfügung. Zudem führt Minitab mit Zielgrößenoptimierung keine Interpolation zwischen den Faktorstufen im Versuchsplan durch. Weitere Informationen zu den Möglichkeiten, das Modell zu nutzen, finden Sie unter Übersicht über gespeicherte Modelle.
p-Wert – Fehlende Anpassung
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
- p-Wert ≤ α: Die fehlende Anpassung ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass das Modell die Beziehung nicht richtig widerspiegelt. Zum Verbessern des Modells müssen Sie möglicherweise Terme hinzufügen oder die Daten transformieren.
- p-Wert > α: Die fehlende Anpassung ist statistisch nicht signifikant
-
Wenn der p-Wert größer als das Signifikanzniveau ist, wird mit dem Test keine fehlende Anpassung erkannt.
