Tabelle der Varianzanalyse für Binäre Antwort für faktoriellen Versuchsplan analysieren

Hier finden Sie Definitionen und Anleitungen zur Interpretation für alle Statistiken in der Tabelle der Varianzanalyse.

In diesem Thema

DF
Seq Abw
Beitrag
Kor Abw
Kor MW

Chi-Quadrat
P-Wert – Modell
p-Wert – Term
p-Wert – Krümmung

DF

Die Gesamt-Freiheitsgrade (DF) entsprechen der Menge an Informationen in Ihren Daten. In der Analyse werden diese Informationen verwendet, um die Werte der Koeffizienten zu schätzen. Die Gesamt-DF sind 1 weniger als die Anzahl der Zeilen in den Daten. Die DF für einen Term geben an, wie viele Koeffizienten von dem betreffenden Term verwendet werden. Durch Vergrößern der Anzahl von Termen im Modell werden dem Modell mehr Koeffizienten hinzugefügt, wodurch die DF für Fehler abnehmen. Die DF für Fehler sind die verbleibenden Freiheitsgrade, die im Modell nicht verwendet werden.

Hinweis

Für einen zweistufigen faktoriellen Versuchsplan oder einen Plackett-Burman-Versuchsplan gilt: Wenn ein Versuchsplan Zentralpunkte aufweist, ist ein Freiheitsgrad für den Test auf Krümmung vorgesehen. Wenn der Term für Zentralpunkte im Modell enthalten ist, stellt die Zeile für Krümmung einen Bestandteil des Modells dar. Wenn der Term für Zentralpunkte nicht im Modell enthalten ist, ist die Zeile für Krümmung Bestandteil des Fehlers, mit dem die Terme im Modell getestet werden. In Wirkungsflächenversuchsplänen und definitiven Screening-Versuchsplänen können Sie quadrierte Terme schätzen, so dass der Test auf Krümmung unnötig ist.

Seq Abw

Die sequenzielle Abweichung ist ein Maß für die Abweichung verschiedener Komponenten des Modells. Im Unterschied zur korrigierten Abweichung hängt die sequenzielle Abweichung von der Reihenfolge ab, in der die Terme in das Modell aufgenommen werden. In der Abweichungstabelle verteilt Minitab die sequenzielle Abweichung auf verschiedene Komponenten, die die auf unterschiedliche Quellen zurückzuführende Abweichung beschreiben.

Modell: Mir der sequenziellen Abweichung für das Regressionsmodell wird quantifiziert, in welchem Maß die Gesamtabweichung durch das Modell erklärt wird.

Term: Mit der sequenziellen Abweichung für einen Term wird die Differenz zwischen einem Modell mit einem bestimmten Term und dem Modell ohne diesen Term quantifiziert.
Fehler: Mit der sequenziellen Abweichung für Fehler wird die Abweichung quantifiziert, die durch das Modell nicht erklärt wird.
Gesamt: Die sequenzielle Gesamtabweichung ist die Summe der sequenziellen Abweichung für das Modell und der sequenziellen Abweichung für Fehler. Die sequenzielle Gesamtabweichung quantifiziert die Gesamtabweichung in den Daten.

Interpretation

Wenn Sie die Verwendung der sequenziellen Abweichung für Tests festlegen, verwendet Minitab die sequenzielle Abweichung, um die p-Werte für das Regressionsmodell und die einzelnen Terme zu berechnen. Im Allgemeinen interpretieren Sie die p-Werte und nicht die sequenzielle Abweichung.

Beitrag

Mit dem Beitrag wird der prozentuelle Beitrag jeder Quelle in der ANOVA-Tabelle zur sequenziellen Gesamtabweichung angezeigt.

Interpretation

Höhere Prozentsätze geben an, dass die Quelle einen größeren Teil der Abweichung in der Antwortvariablen beiträgt. Der prozentuelle Beitrag für das Regressionsmodell entspricht dem R² der Abweichung.

Kor Abw

Die korrigierten Abweichungen sind Maße für die Streuung für verschiedene Komponenten des Modells. Die Reihenfolge der Prädiktoren im Modell wirkt sich nicht auf die Berechnung der korrigierten Abweichungen aus. In der Abweichungstabelle verteilt Minitab die Abweichung auf verschiedene Komponenten, die die auf unterschiedliche Quellen zurückzuführende Abweichung beschreiben.

Modell: Mit der korrigierten Abweichung für das Regressionsmodell wird die Differenz zwischen dem aktuellen Modell und dem konstanten Modell quantifiziert.
Term: Mit der korrigierten Abweichung für einen Term wird die Differenz zwischen einem Modell mit dem Term und einem Modell ohne den Term quantifiziert.
Fehler: Mit der korrigierten Abweichung für Fehler wird die Abweichung quantifiziert, die durch das Modell nicht erklärt wird.
Gesamt: Die korrigierte Gesamtabweichung ist die Summe der korrigierten Abweichung für das Modell und der korrigierten Abweichung für Fehler. Die korrigierte Gesamtabweichung quantifiziert die Gesamtabweichung in den Daten.

Interpretation

Minitab verwendet die korrigierten Abweichungen, um den p-Wert für einen Term zu berechnen. Außerdem verwendet Minitab die korrigierten Abweichungen, um das R² der Abweichung zu berechnen. Im Allgemeinen interpretieren Sie die p-Werte sowie das R² und nicht die Abweichungen.

Kor MW

Die korrigierte mittlere Abweichung ist ein Maß dafür, wie viel Abweichung ein Term oder Modell für jeden Freiheitsgrad erklärt. Bei der Berechnung der korrigierten mittleren Abweichung für jeden Term wird davon ausgegangen, dass alle anderen Terme im Modell enthalten sind.

Interpretation

Minitab verwendet den Chi-Quadrat-Wert, um den p-Wert für einen Term zu berechnen. Im Allgemeinen interpretieren Sie die p-Werte und nicht das korrigierte Mittel der Quadrate.

Chi-Quadrat

Jeder Term in der ANOVA-Tabelle weist einen Chi-Quadrat-Wert auf. Der Chi-Quadrat-Wert ist die Teststatistik, mit der bestimmt wird, ob eine Assoziation zwischen einem Term oder Modell und der Antwortvariablen besteht.

Interpretation

Minitab verwendet die Chi-Quadrat-Statistik zum Berechnen des p-Werts, anhand dessen Sie eine Entscheidung über die statistische Signifikanz der Terme und des Modells treffen können. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft. Eine hinreichend große Chi-Quadrat-Statistik führt zu einem kleinen p-Wert, der darauf hinweist, dass der Term oder das Modell statistisch signifikant ist.

P-Wert – Modell

Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.

Interpretation

Um festzustellen, ob die Daten Anzeichen darauf aufweisen, dass sich mindestens ein Koeffizient im Regressionsmodell von 0 unterscheidet, vergleichen Sie den p-Wert für die Regression mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese für den p-Wert für das Modell besagt, dass sämtliche Koeffizienten für Terme im Regressionsmodell gleich 0 sind. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass sich mindestens ein Koeffizient von 0 unterscheidet, während tatsächlich alle Koeffizienten gleich 0 sind, von 5 %.

p-Wert ≤ α: Mindestens ein Koeffizient unterscheidet sich von 0: Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass sich mindestens ein Koeffizient von 0 unterscheidet.
p-Wert > α: Es liegen keine ausreichenden Anzeichen für die Schlussfolgerung vor, dass sich mindestens ein Koeffizient von 0 unterscheidet: Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass sich mindestens ein Koeffizient von 0 unterscheidet. Möglicherweise empfiehlt es sich, ein neues Modell anzupassen.

Die Tests in der Abweichungstabelle sind Likelihood-Quotienten-Tests. Die Tests in der erweiterten Anzeige der Koeffiziententabelle sind Wald-Approximationstests. Die Likelihood-Quotienten-Tests sind bei kleineren Stichproben genauer als Wald-Approximationstests.

p-Wert – Term

Interpretation

Um zu bestimmen, ob die Assoziation zwischen der Antwortvariablen und jedem Term im Modell statistisch signifikant ist, vergleichen Sie den p-Wert für den Term mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass keine Assoziation zwischen dem Term und der Antwortvariablen besteht. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko, dass auf eine vorhandene Assoziation geschlossen wird, während tatsächlich keine vorhanden ist, von 5 %.

p-Wert ≤ α: Die Assoziation ist statistisch signifikant: Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht.
p-Wert > α: Die Assoziation ist statistisch nicht signifikant: Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Es empfiehlt sich möglicherweise, das Modell ohne den Term erneut anzupassen.; Wenn mehrere Prädiktoren ohne eine statistisch signifikante Assoziation mit der Antwortvariablen vorhanden sind, können Sie das Modell reduzieren, indem Sie Terme einzeln nacheinander entfernen. Weitere Informationen zum Entfernen von Termen aus dem Modell finden Sie unter Modellreduzierung.

Wenn ein Modellterm statistisch signifikant ist, hängt die Interpretation von der Art des Terms ab. Die Interpretationen lauten wie folgt:

Wenn ein stetiger Faktor signifikant ist, können Sie schlussfolgern, dass sich der Koeffizient für den Faktor von null unterscheidet.
Wenn ein kategorialer Faktor signifikant ist, können Sie schlussfolgern, dass die Wahrscheinlichkeit des Ereignisses nicht für alle Stufen des Faktors gleich ist.
Wenn ein Wechselwirkungsterm signifikant ist, können Sie schlussfolgern, dass die Beziehung zwischen einem Faktor und der Wahrscheinlichkeit des Ereignisses von den anderen Faktoren im Term abhängt.
Wenn ein quadratischer Term signifikant ist, können Sie schlussfolgern, dass die Wirkungsfläche eine Krümmung aufweist.

Die Tests in der Tabelle der Varianzanalyse sind Likelihood-Quotienten-Tests. Die Tests in der erweiterten Anzeige der Koeffiziententabelle sind Wald-Approximationstests. Die Likelihood-Quotienten-Tests sind bei kleineren Stichproben genauer als Wald-Approximationstests.

p-Wert – Krümmung

Minitab führt einen Test auf Krümmung durch, wenn der Versuchsplan Zentralpunkte aufweist. Im Test wird der angepasste Mittelpunkt der Antwortvariablen bei den Zentralpunkten im Vergleich mit dem Mittelpunkt untersucht, der zu erwarten wäre, wenn die Beziehungen zwischen den Modelltermen und der Antwortvariablen linear wäre. Verwenden Sie Faktordiagramme, um die Krümmung grafisch zu veranschaulichen.

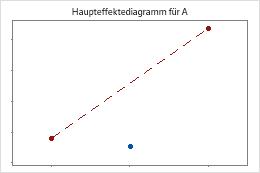
Die Zentralpunkte liegen weit entfernt von der Linie, die die Mittelwerte der Eckpunkte verbindet, was auf eine gekrümmte Beziehung hinweist. Verwenden Sie den p-Wert, um zu prüfen, ob die Krümmung statistisch signifikant ist.

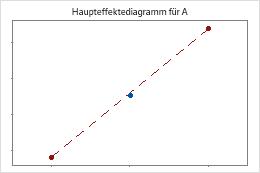
Die Zentralpunkte liegen dicht an der Linie, die die Mittelwerte der Eckpunkte verbindet. Die Krümmung ist wahrscheinlich statistisch nicht signifikant.

Interpretation

Um zu bestimmen, ob sich mindestens einer der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen befindet, vergleichen Sie den p-Wert für Krümmung mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass alle Beziehungen zwischen den Faktoren und der Antwortvariablen linear sind.

In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 % für die Schlussfolgerung an, dass sich die Antwortvariable durch unterschiedliche Bedingungen bei den einzelnen Durchläufen ändert, während dies tatsächlich nicht der Fall ist.

p-Wert ≤ α: Mindestens ein Faktor befindet sich in einer gekrümmten Beziehung mit der Antwortvariablen: Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, schlussfolgern Sie, dass sich mindestens einer der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen befindet. Es empfiehlt sich, dem Versuchsplan Sternpunkte hinzuzufügen, um auf diese Weise die Krümmung zu modellieren.
p-Wert > α: Es liegen keine ausreichenden Anzeichen für die Schlussfolgerung vor, dass einer der Faktoren über eine gekrümmte Beziehung mit der Antwortvariablen verfügt: Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass einer oder mehrere der Faktoren in einer gekrümmten Beziehung mit der Antwortvariablen steht. Wenn die Krümmung Teil des Modells ist, empfiehlt es sich möglicherweise, das Modell ohne einen Term für Zentralpunkte neu anzupassen, so dass die Krümmung Teil des Fehlers ist.

Hinweis

Wenn die Krümmung statistisch nicht signifikant ist, entfernen Sie im Allgemeinen den Zentralpunktterm. Wenn Sie die Zentralpunkte im Modell belassen, geht Minitab davon aus, dass das Modell eine Krümmung aufweist, die für den faktoriellen Versuchsplan nicht passend ist. Aufgrund der unzureichenden Anpassung stehen die Optionen Konturdiagramm, Wirkungsflächendiagramm und Überlagertes Konturdiagramm nicht zur Verfügung. Zudem führt Minitab mit Zielgrößenoptimierung keine Interpolation zwischen den Faktorstufen im Versuchsplan durch. Weitere Informationen zu den Möglichkeiten, das Modell zu nutzen, finden Sie unter Übersicht über gespeicherte Modelle.