Alle Prozessfähigkeitsberichte für Prozessbericht

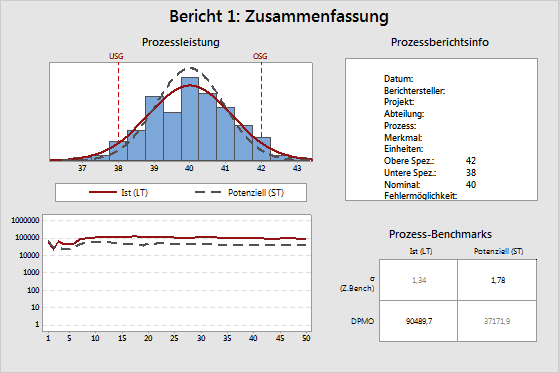
Oberes Diagramm der Prozessleistung: Statische Prozessleistung LT/ST

Die Normalverteilungskurven im Histogramm zeigen die geschätzte Verteilung der Messwerte der Projekt-CTQs. Bei CTQs (Critical-to-Quality) handelt es sich um primär messbare Merkmale eines Produkts oder Prozesses, deren Leistungsstandards erfüllt werden müssen, um den Kunden zufriedenzustellen. CTQs können sich auf eine beliebige Variable beziehen, die mit dem Produkt oder der Dienstleistung verbunden ist, und sie können eine obere und eine untere Spezifikationsgrenze aufweisen.

Minitab berechnet diese Kurven aus den Langzeit- (LT, Long-Term) und Kurzzeitschätzwerten (ST, Short-Term) des Prozessmittelwerts und der Prozessstandardabweichung. Anschließend zeichnet Minitab eine LT- und eine ST-Normalverteilungskurve. In fast allen Fällen ist die LT-Normalverteilungskurve breiter als die ST-Normalverteilungskurve.

Die Spezifikationsgrenzen (USG und OSG) dienen als Referenzpunkte. Der Sollwert (Nominalwert) ist meist, jedoch nicht immer, zwischen der unteren und der oberen Spezifikationsgrenze zentriert. Idealerweise sollte der Mittelwert nahe am Sollwert liegen. Im obigen Beispiel liegt der Prozessmittelwert anscheinend sehr nah am Sollwert.

Unteres Diagramm der Prozessleistung: Dynamische Prozessleistung LT/ST

In diesem Diagramm wird der geschätzte kumulative DPMO (Fehler pro Million Möglichkeiten) nach jeder Teilgruppe von Daten angezeigt, sowohl für LT (Long-Term) als auch für ST (Short-Term). Minitab berechnet den DPMO durch Bestimmen eines Z.Bench-Werts nach jeder Teilgruppe, der in einen DPMO konvertiert wird. Die Z.Bench-Werte sind sowohl für LT als auch für ST Funktionen des geschätzten Mittelwerts und der geschätzten Standardabweichung.

Wenn der Prozess stabil ist, nähern sich die Linien in diesem Diagramm einem stetigen Wert. Wenn der Verlauf der Linien nicht flacher wird, ist entweder der Prozess instabil, oder es liegen keine ausreichenden Daten vor. Im obigen Beispiel weisen beide Linien tendenziell Schwankungen auf der linken Seite des Diagramms auf, die jedoch auf der rechten Seite des Diagramms nach und nach geringer werden. Es kann sich auch zeigen, dass die Linien auf der linken Seite des Diagramms relativ flach sind und anschließend kontinuierlich ansteigen bzw. abfallen. Dies weist darauf hin, dass möglicherweise eine Änderung im Prozess aufgetreten ist: Entweder liegt ein Shift des Mittelwerts vor, oder die Prozessstreuung hat sich geändert. In fast allen Fällen liegt die LT-Linie oberhalb der ST-Linie, da aufgrund des Einflusses von Shift und Drift auf den Prozess Z.Bench (LT) kleiner als Z.Bench (ST) ist.

Beide Linien im Diagramm sollten auf der linken Seite, wo wenige Teilgruppen vorhanden sind, nach oben und unten oszillieren. Ihr Verlauf sollte jedoch auf der rechten Seite flacher werden, wenn ausreichend Daten erfasst wurden und der Prozess stabil ist. Wenn der Verlauf der Linien nicht flacher wird, ziehen Sie die Diagramme in „Bericht 4: Kumulative Statistik“ heran, um zu ermitteln, ob die Menge der Daten nicht ausreicht oder eine Prozessinstabilität vorliegt.

Prozessberichtsinfo

Die Tabelle „Prozessberichtsinfo“ zeigt die von Ihnen angegebenen Projekt- und Prozessinformationen.

Prozess-Benchmarks

Die Zahlen in Fettdruck stellen die Werte von ST-Sigma (oder Z.Bench) und LT-DPMO dar. In den meisten Black-Belt-Prozessleistungsberichten werden diese zwei Werte verwendet.

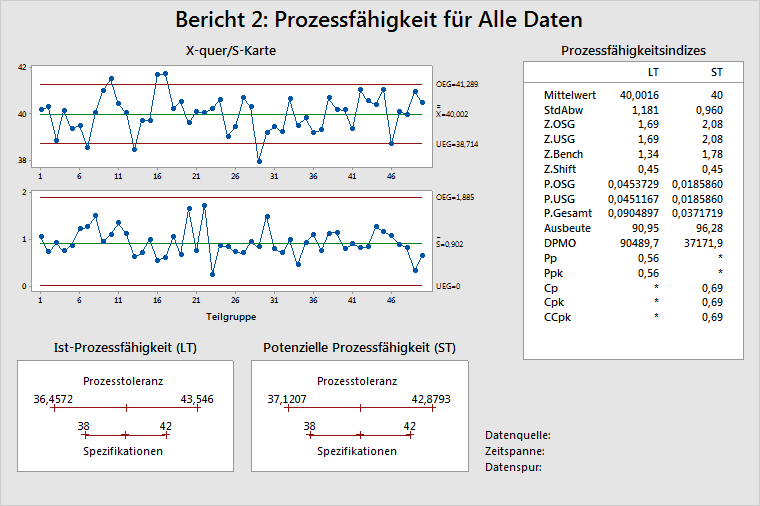
Regelkarten der Prozessdaten

Diese Komponente zeigt die Prozessstabilität für den Zeitraum der Datenerfassung. Verwenden Sie für Teilgruppen größer als 1 eine X-quer-Karte zum Ermitteln der Stabilität des Prozessmittelwerts und eine S-Karte zum Ermitteln der Stabilität der Prozessstandardabweichung. Wenn die Teilgruppengröße gleich 1 ist, zeigt Minitab eine I-Karte und eine MR-Karte an.

Prozessfähigkeitsdiagramme LT/ST

Diese Komponente zeigt die geschätzte Prozesstoleranz in Bezug auf die Spezifikationsgrenzen. Die Prozesstoleranz entspricht dem Zentralpunkt des Prozesses ± 3 Standardabweichungen. Es gibt zwei Diagramme, da der Zentralpunkt des Prozesses und die Prozessstandardabweichung für LT und ST unterschiedlich sind. LT verwendet den Prozessmittelwert als Zentralpunkt, während ST den Sollwert als Zentralpunkt verwendet (oder den Mittelpunkt zwischen den Spezifikationsgrenzen oder, wenn nur eine Spezifikationsgrenze angegeben wurde, den Prozessmittelwert). Weitere Informationen finden Sie unter Auswahl der Zentralwerte für Kurzzeitstatistiken durch Minitab für Prozessbericht.

Anders gesagt, diese Grafiken zeigen, ob ein Fahrzeug (der Prozess) in eine Garage (die Spezifikationsgrenzen) passt bzw. ob das Fahrzeug überhaupt in Richtung Garage zeigt. In dem obigen Beispiel ist der Prozess breiter als die Spezifikationsgrenzen. Der Prozess ist jedoch (wie im LT-Diagramm veranschaulicht) zentriert, und dies weist darauf hin, dass der Zentralpunkt (Mittelpunkt) des Prozesses nahezu dem Sollwert entspricht.

Prozessfähigkeitsindizes LT/ST

Diese Komponente zeigt die Statistiken, mit denen häufig die Prozessleistung dargestellt wird. Einen kontrastiven Vergleich der Statistiken zur Langzeit- (LT) und Kurzzeitleistung (ST) finden Sie unter Grundlagen von Prozessfähigkeitsmaßen.

Beschreiben Sie die Prozessleistung mit Hilfe von Z.Bench-Werten. Die Z.Bench-Statistiken beruhen nicht nur auf den angemessenen Prozessbedingungen, sie führen auch direkt zu Schätzwerten für die Wahrscheinlichkeit von Fehlern wie PPM und DPMO. CCpk und Ppk sind akzeptable Alternativen, da diese auf den gleichen Prozessbedingungen wie die Z.Bench-Statistiken beruhen.

Weitere Informationen zu konkreten Berechnungen finden Sie unter Berechnungen von Prozessstatistiken und Prozessfähigkeitswerten für Prozessbericht.

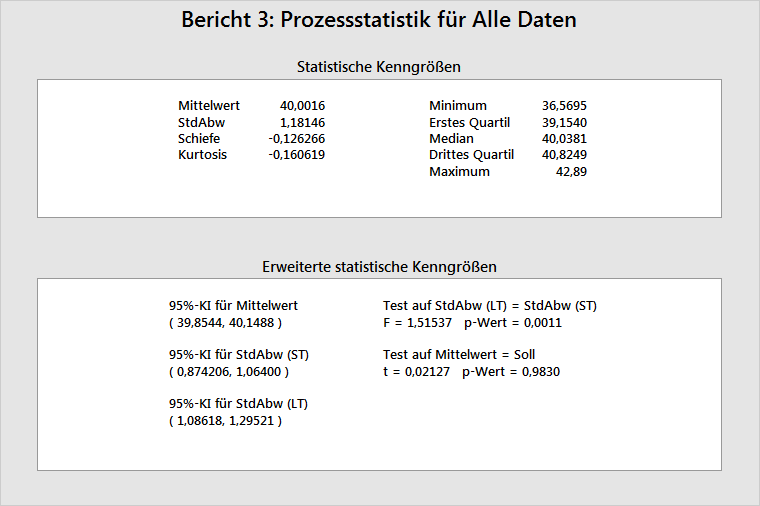
Statistische Kenngrößen

In dieser Tabelle werden der Prozessmittelwert (LT-Mittelwert), die Prozessstandardabweichung (LT-Standardabweichung) sowie weitere statistische Kenngrößen angezeigt.

Ermitteln Sie anhand von Schiefe und Kurtosis, ob die Daten normalverteilt sind. Wahrscheinlichkeitsnetze sind jedoch viel hilfreicher. (In Bericht 6 wird mit dem Wahrscheinlichkeitsnetz (Normal) die Wahrscheinlichkeit eines Fehlers geschätzt.)

Das Minimum, das 1. Quartil, der Median, das 3. Quartil und das Maximum zeigen die Streubreite der Daten. Beispielsweise sind 25 % der Daten nicht größer als 39,1540 (1. Quartil), 50 % der Daten sind nicht größer als 40,0381 (Median), und 75 % der Daten sind nicht größer als 40,8249 (3. Quartil).

Erweiterte statistische Kenngrößen

In dieser Tabelle werden statistische Rückschlüsse für die Prozessparameter, den ST- Mittelwert und die Standardabweichung bereitgestellt.

Der Prozessmittelwert zeigt anhand des 95%-Konfidenzintervalls und der Teststatistiken, ob der Prozessmittelwert gleich dem Sollwert des Prozesses ist. Wenn Prozessmittelwert und Prozesssollwert keinen statistisch signifikanten Unterschied aufweisen, sollte der p-Wert > 0,05 sein und der Prozesssollwert innerhalb der Grenzen des Konfidenzintervalls liegen. Im obigen Beispiel weist der Test einen p-Wert von 0,9830 auf, und der Sollwert (40) befindet sich innerhalb der Grenzen des 95%-Konfidenzintervalls des Mittelwerts. Sie können die Nullhypothese nicht verwerfen, dass der Prozessmittelwert dem Prozesssollwert entspricht.

Die Tabelle enthält zudem 95%-Konfidenzintervalle für die LT- und ST-Standardabweichungen sowie einen Test, mit denen die beiden Maße auf Gleichheit überprüft werden können. Wenn kein statistisch signifikanter Unterschied zwischen der LT- und der ST-Prozessstandardabweichung besteht, können Sie schlussfolgern, dass der Prozess keinen signifikanten Shift und/oder Drift aufweist und dass beim Erfassen der Daten keine Ausnahmebedingungen vorlagen. Im obigen Beispiel weist der Test auf gleiche Varianzen einen p-Wert von 0,0011 auf. Daher müssen Sie die Nullhypothese zurückweisen und schlussfolgern, dass sich die LT-Standardabweichung und die ST-Standardabweichung signifikant voneinander unterscheiden.

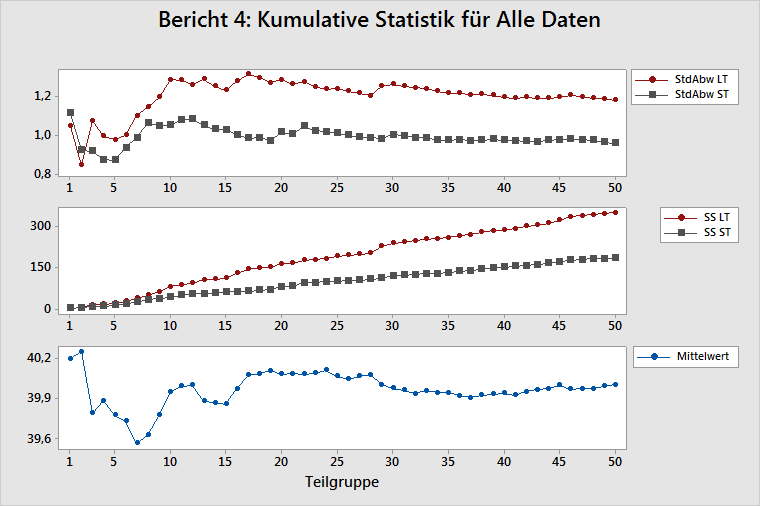
Kumulative StdAbw LT/ST

In diesem Diagramm werden die Schätzwerte der LT-Standardabweichung und der ST-Standardabweichung nach jeder Teilgruppe von Daten angezeigt. Da alle Messwerte der Prozessleistung auf den Schätzwerten der Prozessstandardabweichung beruhen, sollten Sie ermitteln, ob diese Schätzwerte angemessen sind. Dabei werden ein stabiler Prozess (d. h. ein Prozess, in dem sich die inhärente Streuung nicht ändert) und eine ausreichende Datenmenge benötigt, um den Prozess angemessen zu charakterisieren.

Die Schätzwerte der LT-Standardabweichung und der ST-Standardabweichung sollten auf der linken Seite des Diagramms, auf der sich wenige Teilgruppen befinden, erheblich oszillieren. Wenn der Prozess stabil ist und Sie eine ausreichende Menge von Daten erfasst haben, stabilisieren sich die Schätzwerte auf der rechten Seite des Diagramms. Wenn die Linien im Diagramm weiterhin oszillieren, haben Sie entweder keine ausreichende Datenmenge erfasst, oder die Prozessstreuung ist instabil.

Bei einem stabilen Prozess sollte der Abstand zwischen LT- und ST-Standardabweichung relativ konstant sein. Wenn sich der Prozess beispielsweise durch einen Shift des Mittelwerts oder eine Änderung der Streuung ändert, ändert sich der Abstand zwischen der LT- und der ST-Standardabweichung.

Weitere Informationen finden Sie unter Identifizieren von Mittelwert-Shifts mit Prozessbericht und Identifizieren eines Anstiegs der Prozessstreuung mit Prozessbericht.

Kumulative SS LT/ST

In diesem Diagramm werden die Summe der quadrierten Abweichungen (SS Gesamt oder SS LT) nach jeder Teilgruppe von Daten und die Summe aller quadrierten Abweichungen innerhalb jeder Teilgruppe (SS Innerhalb oder SS ST) nach jeder Teilgruppe von Daten angezeigt. Weitere Informationen finden Sie unter Berechnungen für Summen der Quadrate für Prozessbericht.

SS ST stellt ein sehr gutes Analysewerkzeug zum Erkennen von Änderungen in der inhärenten Prozessstreuung dar. Wenn die inhärente Streuung stabil ist, ist SS Innerhalb für jede Teilgruppe ungefähr gleich. Deswegen sollte SS ST für jede Teilgruppe im gleichen Maße ansteigen, woraus sich eine SS ST-Linie mit einer konstanten Aufwärtssteigung ergibt. Jede Änderung in der inhärenten Prozessstreuung zeigt sich als Änderung in der Steigung der SS ST-Linie.

SS Gesamt ist die Summe von SS Innerhalb und SS Zwischen. Somit wird SS Gesamt durch die Stabilität der Prozessvarianz und des Prozessmittelwerts beeinflusst. Wenn beide stabil sind, ist der Beitrag jeder Teilgruppe zu SS Gesamt ungefähr gleich. Daher sollte SS LT für jede Teilgruppe im gleichen Maß ansteigen, woraus sich eine SS LT-Linie mit einer konstanten Aufwärtssteigung ergibt. Jede Änderung in der inhärenten Prozessstreuung zeigt sich als Änderung in der Steigung der SS LT-Linie.

Eine plötzliche Änderung der inhärenten Prozessstreuung beeinflusst SS Innerhalb und SS Zwischen und wirkt sich auf die Steigungen der SS ST- und SS LT-Linien aus. Deswegen weist eine Änderung der Steigung beider Linien auf eine Änderung der inhärenten Prozessstreuung hin.

Ein Shift des Prozessmittelwerts beeinflusst SS Zwischen, jedoch nicht SS Innerhalb, und ändert daher die Steigung der SS LT-Linie, jedoch nicht die der SS ST-Linie. Deswegen weist eine Änderung der Steigung der SS LT-Linie ohne eine Änderung der Steigung der SS ST-Linie auf einen Shift des Prozessmittelwerts hin.

Weitere Informationen finden Sie unter Identifizieren von Mittelwert-Shifts mit Prozessbericht und Identifizieren eines Anstiegs der Prozessstreuung mit Prozessbericht.

Kumulierter Mittelwert

In diesem Diagramm wird der Schätzwert des Prozessmittelwerts nach jeder Teilgruppe angezeigt. Die Angemessenheit des Schätzwerts des Prozessmittelwerts hängt von der Menge der erfassten Daten sowie von der Stabilität des Prozesses ab.

Die Schätzwerte sollten auf der linken Seite des Diagramms, auf der sich nur wenige Teilgruppen befinden, erheblich auf- und abwärts oszillieren. Wenn der Prozess stabil ist und Sie eine ausreichende Menge von Daten erfasst haben, stabilisieren sich die Schätzwerte auf der rechten Seite des Diagramms. Wenn die Linien im Diagramm weiterhin oszillieren, haben Sie entweder keine ausreichende Datenmenge erfasst, oder der Prozessmittelwert weist einen erheblichen Drift auf. Betrachten Sie das Diagramm der kumulativen Standardabweichung, um festzustellen, ob das Problem darauf zurückzuführen ist, dass keine ausreichende Datenmenge erfasst wurde. Wenn keine ausreichende Datenmenge vorhanden ist, oszillieren die LT-Linie und die ST-Linie ebenfalls.

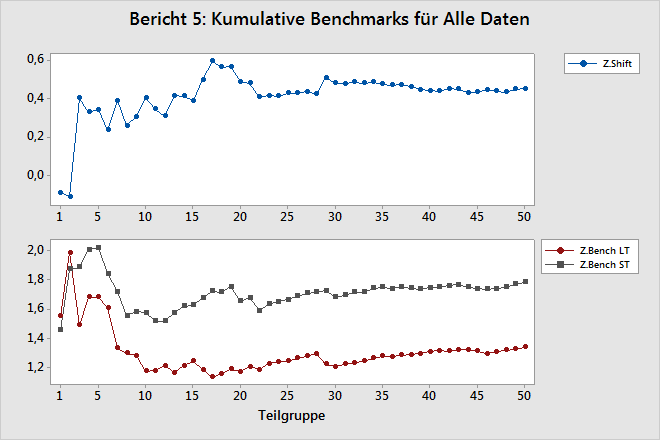
Z.Shift

Z.Shift ist gleich dem Abstand zwischen Z.Bench LT und Z.Bench ST.

Die Linie im Diagramm sollte auf der linken Seite, auf der sich wenige Teilgruppen befinden, nach oben und unten oszillieren. Sie sollte sich jedoch auf der rechten Seite stabilisieren, nachdem eine ausreichende Datenmenge erfasst wurde und der Prozess stabil ist.

Z.Bench LT und Z.Bench ST

Dem Z.Bench-Diagramm können Sie entnehmen, ob Sie ausreichend Daten erfasst haben, um diese Statistik als aussagekräftig zu betrachten und die Prozessleistung darstellen zu können. Beide Linien im Diagramm sollten auf der linken Seite, auf der sich wenige Teilgruppen befinden, nach oben und unten oszillieren. Sie sollten sich jedoch auf der rechten Seite stabilisieren, nachdem eine ausreichende Datenmenge erfasst wurde und der Prozess stabil ist. Wenn der Verlauf der Linien nicht flacher wird, können Sie anhand der Diagramme im Bericht „Kumulative Statistik“ ermitteln, ob das Problem auf eine unzureichende Datenmenge oder auf die Instabilität des Prozesses zurückzuführen ist.

Der Abstand im Z.Bench-Diagramm und die Linie im Z.Shift-Diagramm sollten sich beide wie im obigen Beispiel einem konstanten Wert annähern.

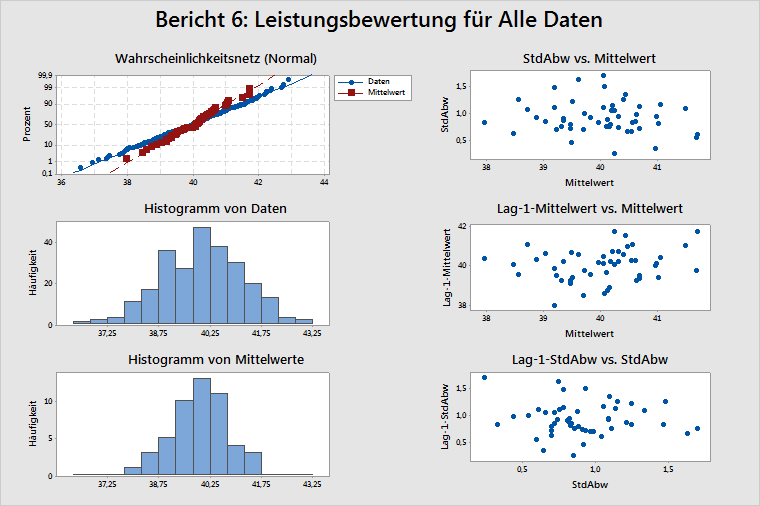
Wahrscheinlichkeitsnetz (Normal), Histogramm der Daten und Histogramm der Mittelwerte

Anhand dieser Diagramme können Sie feststellen, ob Ihre Daten normalverteilt sind. Wenn die Daten nicht normalverteilt sind, sind die Schätzwerte der Wahrscheinlichkeit eines Fehlers (z. B. DPMO) nicht genau. In den meisten Fällen sind diese Schätzwerte tendenziell kleiner als die tatsächlichen Werte. Untersuchen Sie daher das Wahrscheinlichkeitsnetz (Normal) und die zwei Histogramme, um zu prüfen, ob die Daten zumindest ausreichend normalverteilt sind, bevor Sie Schätzwerte wie DPMO verwenden. Die Daten im obigen Beispiel scheinen normalverteilt zu sein.

Wenn die Daten offensichtlich sehr schief sind, sollten Sie versuchen, das Problem mit einer Transformation wie der Box-Cox-Transformation zu beheben. Wenn Sie die Option Box-Cox-Potenztransformation (W=Y^λ) verwenden mit im Unterdialogfeld Prozessbericht Optionen auswählen, transformiert Minitab die Daten, den Sollwert und die Spezifikationsgrenzen automatisch. Wenn Sie die Daten jedoch manuell transformieren, müssen Sie auch den Sollwert und die Spezifikationsgrenzen manuell transformieren.

StdAbw vs. Mittelwert

Wenn zwischen den Mittelwerten und Standardabweichungen der Teilgruppe keine Korrelation vorliegt, sollten in diesem Diagramm zufällig verstreute Punkte angezeigt werden (siehe obiges Beispiel).

Wenn zwischen den Mittelwerten und den Standardabweichungen eine positive Korrelation vorliegt, ist bei den Teilgruppenstandardabweichungen bei ansteigenden Teilgruppenmittelwerten tendenziell ein Anstieg zu beobachten. Die Box-Cox-Transformation (λ = 0) ist eine gängige varianzstabilisierende Transformation, die in solchen Fällen normalerweise gut geeignet ist.

Lag-1-Mittelwert vs. Mittelwert

Lag-1-Mittelwert vs. Mittelwert ist ein Diagramm des Mittelwerts von Teilgruppe_i im Vergleich zum Mittelwert von Teilgruppe_i–1. Dieses Diagramm sollte wie im obigen Beispiel zufällig gestreute Punkte enthalten, was darauf hinweist, dass zwischen aufeinander folgenden Teilgruppenmittelwerten keine Korrelation vorliegt.

Wenn eine positive Korrelation vorliegt und ein Teilgruppenmittelwert größer als der Gesamtmittelwert des Prozesses ist, liegt der folgende Teilgruppenmittelwert wahrscheinlich ebenfalls über dem Gesamtmittelwert des Prozesses. Somit impliziert eine positive Korrelation, dass der Mittelwert im Prozess einen Drift aufweist. Wenn die Korrelation negativ ist, weist dies auf schwankende Teilgruppenmittelwerte (niedrig, dann hoch, dann wieder niedrig) und nicht auf zwei aufeinander folgende niedrige Teilgruppenmittelwerte hin. Diese negative Korrelation impliziert eine übermäßige Kontrolle des Prozesses.

Lag-1-StdAbw vs. StdAbw

Lag-1-StdAbw vs. StdAbw ist ein Diagramm der Standardabweichung von Teilgruppe_i im Vergleich zur Standardabweichung von Teilgruppe_i–1. Dieses Diagramm sollte wie im obigen Beispiel zufällig gestreute Punkte enthalten, was darauf hinweist, dass zwischen aufeinander folgenden Teilgruppenstandardabweichungen keine Korrelation vorliegt.

Ähnlich wie bei den Teilgruppenmittelwerten gilt: Wenn eine positive Korrelation vorliegt und die Standardabweichung für eine Teilgruppe größer als die durchschnittliche Standardabweichung für alle Teilgruppen ist, liegt die Standardabweichung für die folgende Teilgruppe wahrscheinlich ebenfalls über der durchschnittlichen Standardabweichung für alle Teilgruppen. Deswegen zeigen Teilgruppenstandardabweichungen tendenziell einen Aufwärts- bzw. Abwärtsdrift. Diese Bedingung kann mit Mittelwerten einhergehen, die ebenso einen Aufwärts- bzw. Abwärtsdrift aufweisen, sowie mit einer Korrelation zwischen den Teilgruppenmittelwerten und den Teilgruppenstandardabweichungen. Verwenden Sie in diesem Fall eine Box-Cox-Transformation mit λ = 0.

Eine positive Autokorrelation der Teilgruppenstandardabweichungen kann durch Werkzeugverschleiß oder andere Abnutzungserscheinungen im Prozess (die zu einer stetig ansteigenden Streuung führen) oder durch das Vorhandensein eines unkontrollierten Störfaktors (z. B. die relative Luftfeuchtigkeit) mit Einfluss auf die Streuung verursacht werden.