In diesem Thema
Systematische Messabweichung
Die systematische Messabweichung ist die Differenz zwischen dem Referenzwert des Teils und den vom Prüfer für das Teil erfassten Messwerten.
Formel
Durchschnittliche systematische Messabweichung für jedes Teil:
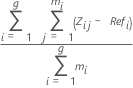
Notation
| Begriff | Beschreibung |
|---|---|
| zi,j | j-ter Messwert des i-ten Teils |
| Refi | Referenzwert des i-ten Teils |
| mi | Anzahl der Replikationen des i-ten Teils |
%systematische Messabweichung
„%systematische Messabweichung“ ist die systematische Messabweichung ausgedrückt als Prozentsatz der Gesamtprozessstreuung.
Formeln
%systematische Messabweichung = 100 * (|Durchschnittliche systematische Messabweichung| / Prozessstreuung)
Notation
| Begriff | Beschreibung |
|---|---|
| zi,j | j-ter Messwert des i-ten Teils |
| Refi | Referenzwert des i-ten Teils |
| mi | Anzahl der Replikationen des i-ten Teils |
p-Wert für Untersuchung von Linearität und systematischer Messabweichung
Prüfen Sie anhand der p-Werte, ob die systematische Messabweichung bei jedem Referenzwert gleich 0 und die durchschnittliche systematische Messabweichung gleich 0 ist.
Der p-Wert ist als die Fläche unter der Stichprobenverteilung rechts von + |Teststatistik| und die Fläche unter der Stichprobenverteilung links von - |Teststatistik| definiert. Der p-Wert in der Ausgabe wird anhand der t-Verteilung mit γ df und der t-Statistik berechnet.
Minitab bietet spezielle Berechnungen der t-Statistik für die Methode auf der Grundlage der Spannweite der Stichprobe und für die Methode auf der Grundlage der Standardabweichung der Stichprobe.
Methode mit Spannweite der Stichprobe
Minitab verwendet entweder die Spannweite der Stichprobe (Standard) oder die Standardabweichung der Stichprobe, um die Standardabweichung der Wiederholbarkeit zu schätzen. Mit der Standardabweichung der Wiederholbarkeit wird der t-Wert berechnet, der Grundlage für die Berechnung des p-Werts ist, mit dem getestet wird, ob die systematische Messabweichung für alle Referenzwerte und für jeden einzelnen Referenzwert gleich 0 ist.
Formeln
Für die Methode mit der Spannweite der Stichprobe gilt für die Standardabweichung der Wiederholbarkeit, wenn jeder eindeutige Referenzwert einem eindeutigen Teil entspricht:
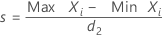
Wenn mehrere Teile denselben Referenzwert aufweisen, gilt für die Standardabweichung der Wiederholbarkeit:

Die t-Statistik zum Testen auf systematische Messabweichung lautet wie folgt:
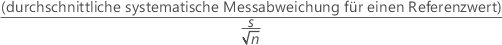
Die Freiheitsgrade (γ) stammen aus einer Tabelle im AIAG-Handbuch1. Minitab verwendet die t-Verteilung mit γ df und dem t-Wert, um den p-Wert zu berechnen.
Notation
| Begriff | Beschreibung |
|---|---|
| Xi | systematische Messabweichung des i-ten Messwerts für ein Teil |
| d2 | Wert aus einer Tabelle1, wobei der Stichprobenumfang = n |
 | durchschnittliche Spannweite |
Methode mit Standardabweichung der Stichprobe
Minitab verwendet entweder die Spannweite der Stichprobe (Standard) oder die Standardabweichung der Stichprobe, um die Standardabweichung der Wiederholbarkeit zu schätzen. Mit der Standardabweichung der Wiederholbarkeit wird der t-Wert berechnet, der Grundlage für die Berechnung des p-Werts ist, mit dem getestet wird, ob die systematische Messabweichung gleich 0 ist.
Formeln
Für die Methode mit der Standardabweichung der Stichprobe gilt für die Standardabweichung der Wiederholbarkeit, wenn ein Referenzwert einem einzigen Teil entspricht:

Die t-Statistik zum Testen auf systematische Messabweichung lautet wie folgt:
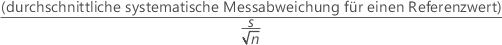
Es liegen n – 1 Freiheitsgrade vor. Der p-Wert in der Ausgabe wird aus der t-Verteilung mit dem t-Wert und den Freiheitsgraden berechnet.
Wenn mehrere Teile denselben Referenzwert aufweisen, ist die Standardabweichung der Wiederholbarkeit die zusammengefasste Stichprobenstandardabweichung s für alle Teile mit demselben Referenzwert:

Die t-Statistik zum Testen auf systematische Messabweichung lautet wie folgt:

Die Freiheitsgrade sind (n1- 1) + ... + (ng - 1). Der p-Wert in der Ausgabe wird aus der t-Verteilung mit dem t-Wert und den Freiheitsgraden berechnet.
Notation
| Begriff | Beschreibung |
|---|---|
| x | i-ter Messwert des Teils |
 | durchschnittlicher Messwert für das Teil |
| n | Stichprobenumfang |
| S1 | Standardabweichung der Stichprobe für Teil 1 mit n1 Messwerten |
| Sg | Standardabweichung der Stichprobe für Teil g mit ng Messwerten |
