Support für Minitab® 

Methoden und Formeln für Regelkarte der gleitenden Spannweite (MR)

Weitere Informationen zu Minitab
Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Dargestellte Punkte

Jeder Datenpunkt MRi ist die gleitende Spannweite der x-Werte in jeder Gruppe. MR i wird für i < w nicht dargestellt, da dieser Wert nicht definiert ist.

Notation

BegriffBeschreibung
MRgleitende Spannweite
w Anzahl der Beobachtungen in der gleitenden Spannweite. Standardmäßig ist w = 2.

Mittellinie

Die Mittellinie ist der erwartungstreue Schätzwert des Durchschnitts der gleitenden Spannweiten.

Wenn der durchschnittliche gleitende Bereich zur Schätzung der Standardabweichung verwendet wird, ist die Mittellinie = MR

Wenn der mittlere gleitende Bereich zur Schätzung der Standardabweichung verwendet wird, ist die Mittellinie = d2(w) * MR.

Notation

HERR
Schätzwert der durchschnittlichen gleitenden Spannweite für die Methode, mit der die Standardabweichung geschätzt wird
D2(W)
eine unverzerrte Konstante
w
Anzahl der Beobachtungen in der gleitenden Spannweite

Eingriffsgrenzen

Untere Eingriffsgrenze (UEG)

Die UEG ist der größere der folgenden Werte:

oder

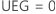
Obere Eingriffsgrenze (OEG)

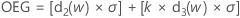
Notation

BegriffBeschreibung
d2() eine Konstante zum Schätzen der Standardabweichung
wAnzahl der Beobachtungen in der gleitenden Spannweite. Standardmäßig ist w = 2.
σ Standardabweichung des Prozesses
k Parameter für Test 1 (Standardwert ist 3)
d3() eine Konstante zum Schätzen der UEG und OEG

Methode: Mittelwert der gleitenden Spannweite

Der Mittelwert der gleitenden Spannweite, , mit der Länge w wird mit der folgenden Formel angegeben:

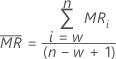
wobei MRi die gleitende Spannweite für Beobachtung i darstellt, die wie folgt berechnet wird:

Minitab verwendet zum Berechnen von Smr, einem erwartungstreuen Schätzwert von σ:

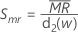
Notation

BegriffBeschreibung
nAnzahl der Beobachtungen
w Länge der gleitenden Spannweite. Der Standardwert ist 2.
d2() Wert der Konstanten für erwartungstreue Schätzung d2, der dem in Klammern angegebenen Wert entspricht

Methode: Median der gleitenden Spannweite

Der Median der gleitenden Spannweite, , mit der Länge w wird mit der folgenden Formel angegeben:

wobei MRi die gleitende Spannweite für Beobachtung i darstellt, die wie folgt berechnet wird:

Minitab verwendet zum Berechnen von Smr, einem erwartungstreuen Schätzwert von σ:

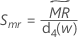
Notation

BegriffBeschreibung
nAnzahl der Beobachtungen
w Länge der gleitenden Spannweite. Der Standardwert ist 2.
d4() Wert der Konstanten für erwartungstreue Schätzung d4, der dem in Klammern angegebenen Wert entspricht

Konstanten für erwartungstreue Schätzung d2(), d3() und d4()

d2(N) ist der erwartete Wert der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit Standardabweichung = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist E(r) = d2(N)σ.

d3(N) ist die Standardabweichung der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit σ = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist StdAbw(r) = d3(N)σ.

Suchen Sie in der folgenden Tabelle eine Konstante für die erwartungstreue Schätzung für einen bestimmten Wert N. (Ziehen Sie zum Bestimmen des Werts von N die Formel für die betreffende Statistik hinzu.)

Verwenden Sie für Werte von N von 51 bis 100 die folgende Approximation für d2(N):
Verwenden Sie für Werte von N von 26 bis 100 die folgenden Approximationen für d3(N) und d4(N):
Weitere Informationen zu diesen Konstanten finden Sie in folgenden Veröffentlichungen:
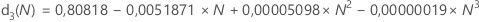
  • D. J. Wheeler und D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
  • H. Leon Harter (1960). „Tables of Range and Studentized Range“. The Annals of Mathematical Statistics, Vol. 31, Nr. 4, Institute of Mathematical Statistics, S. 1122−1147.
Tabelle 1. Tabelle der Werte
N d2(N) d3(N) d4(N)
2 1,128 0,8525 0,954
3 1,693 0,8884 1,588
4 2,059 0,8798 1,978
5 2,326 0,8641 2,257
6 2,534 0,848 2,472
7 2,704 0,8332 2,645
8 2,847 0,8198 2,791
9 2,970 0,8078 2,915
10 3,078 0,7971 3,024
11 3,173 0,7873 3,121
12 3,258 0,7785 3,207
13 3,336 0,7704 3,285
14 3,407 0,7630 3,356
15 3,472 0,7562 3,422
16 3,532 0,7499 3,482
17 3,588 0,7441 3,538
18 3,640 0,7386 3,591
19 3,689 0,7335 3,640
20 3,735 0,7287 3,686
21 3,778 0,7242 3,730
22 3,819 0,7199 3,771
23 3,858 0,7159 3,811
24 3,895 0,7121 3,847
25 3,931 0,7084 3,883
N d2(N)
26 3,964
27 3,997
28 4,027
29 4,057
30 4,086
31 4,113
32 4,139
33 4,165
34 4,189
35 4,213
36 4,236
37 4,259
38 4,280
39 4,301
40 4,322
41 4,341
42 4,361
43 4,379
44 4,398
45 4,415
46 4,433
47 4,450
48 4,466
49 4,482
50 4,498

Konstante für erwartungstreue Schätzung c4'()

Entnehmen Sie den folgenden Tabellen Werte für die Konstante für die erwartungstreue Schätzung c4'(), die in den Formeln für die Schätzmethode für Sigma auf der Grundlage der Quadratwurzel von MSSD verwendet wird.

N c4'(N) N c4'(N) N c4'(N)
2 0,797850 41 0,990797 80 0,995215
3 0,871530 42 0,991013 81 0,995272
4 0,905763 43 0,991218 82 0,995328
5 0,925222 44 0,991415 83 0,995383
6 0,937892 45 0,991602 84 0,995436
7 0,946837 46 0,991782 85 0,995489
8 0,953503 47 0,991953 86 0,995539
9 0,958669 48 0,992118 87 0,995589
10 0,962793 49 0,992276 88 0,995638
11 0,966163 50 0,992427 89 0,995685
12 0,968968 51 0,992573 90 0,995732
13 0,971341 52 0,992713 91 0,995777
14 0,973375 53 0,992848 92 0,995822
15 0,975137 54 0,992978 93 0,995865
16 0,976679 55 0,993103 94 0,995908
17 0,978039 56 0,993224 95 0,995949
18 0,979249 57 0,993340 96 0,995990
19 0,980331 58 0,993452 97 0,996030
20 0,981305 59 0,993561 98 0,996069
21 0,982187 60 0,993666 99 0,996108
22 0,982988 61 0,993767 100 0,996145
23 0,983720 62 0,993866 101 0,996182
24 0,984391 63 0,993961 102 0,996218
25 0,985009 64 0,994053 103 0,996253
26 0,985579 65 0,994142 104 0,996288
27 0,986107 66 0,994229 105 0,996322
28 0,986597 67 0,994313 106 0,996356
29 0,987054 68 0,994395 107 0,996389
30 0,987480 69 0,994474 108 0,996421
31 0,987878 70 0,994551 109 0,996452
32 0,988252 71 0,994626 110 0,996483
33 0,988603 72 0,994699 111 0,996514
34 0,988934 73 0,994769 112 0,996544
35 0,989246 74 0,994838 113 0,996573
36 0,989540 75 0,994905 114 0,996602
37 0,989819 76 0,994970 115 0,996631
38 0,990083 77 0,995034 116 0,996658
39 0,990333 78 0,995096 117 0,996686
40 0,990571 79 0,995156 118 0,996713
N c4'(N) N c4'(N) N c4'(N)
119 0,996739 160 0,997541 201 0,998016
120 0,996765 161 0,997555 202 0,998025
121 0,996791 162 0,997570 203 0,998034
122 0,996816 163 0,997584 204 0,998043
123 0,996841 164 0,997598 205 0,998052
124 0,996865 165 0,997612 206 0,998061
125 0,996889 166 0,997625 207 0,998070
126 0,996913 167 0,997639 208 0,998078
127 0,996936 168 0,997652 209 0,998087
128 0,996959 169 0,997665 210 0,998095
129 0,996982 170 0,997678 211 0,998104
130 0,997004 171 0,997691 212 0,998112
131 0,997026 172 0,997703 213 0,998120
132 0,997047 173 0,997716 214 0,998128
133 0,997069 174 0,997728 215 0,998137
134 0,997089 175 0,997741 216 0,998145
135 0,997110 176 0,997753 217 0,998152
136 0,997130 177 0,997765 218 0,998160
137 0,997150 178 0,997776 219 0,998168
138 0,997170 179 0,997788 220 0,998176
139 0,997189 180 0,997800 221 0,998184
140 0,997209 181 0,997811 222 0,998191
141 0,997227 182 0,997822 223 0,998199
142 0,997246 183 0,997834 224 0,998206
143 0,997264 184 0,997845 225 0,998214
144 0,997282 185 0,997856 226 0,998221
145 0,997300 186 0,997866 227 0,998228
146 0,997318 187 0,997877 228 0,998235
147 0,997335 188 0,997888 229 0,998242
148 0,997352 189 0,997898 230 0,998250
149 0,997369 190 0,997909 231 0,998257
150 0,997386 191 0,997919 232 0,998263
151 0,997402 192 0,997929 233 0,998270
152 0,997419 193 0,997939 234 0,998277
153 0,997435 194 0,997949 235 0,998284
154 0,997450 195 0,997959 236 0,998291
155 0,997466 196 0,997969 237 0,998297
156 0,997481 197 0,997978 238 0,998304
157 0,997497 198 0,997988 239 0,998311
158 0,997512 199 0,997997 240 0,998317
159 0,997526 200 0,998007 241 0,998323
N c4'(N) N c4'(N) N c4'(N)
242 0,998330 283 0,998553 324 0,998720
243 0,998336 284 0,998558 325 0,998723
244 0,998342 285 0,998562 326 0,998727
245 0,998349 286 0,998567 327 0,998730
246 0,998355 287 0,998571 328 0,998734
247 0,998361 288 0,998576 329 0,998737
248 0,998367 289 0,998580 330 0,998740
249 0,998373 290 0,998585 331 0,998744
250 0,998379 291 0,998589 332 0,998747
251 0,998385 292 0,998593 333 0,998751
252 0,998391 293 0,998598 334 0,998754
253 0,998397 294 0,998602 335 0,998757
254 0,998403 295 0,998606 336 0,998761
255 0,998408 296 0,998611 337 0,998764
256 0,998414 297 0,998615 338 0,998767
257 0,998420 298 0,998619 339 0,998770
258 0,998425 299 0,998623 340 0,998774
259 0,998431 300 0,998627 341 0,998777
260 0,998436 301 0,998632 342 0,998780
261 0,998442 302 0,998636 343 0,998783
262 0,998447 303 0,998640 344 0,998786
263 0,998453 304 0,998644 345 0,998790
264 0,998458 305 0,998648 346 0,998793
265 0,998463 306 0,998652 347 0,998796
266 0,998469 307 0,998656 348 0,998799
267 0,998474 308 0,998660 349 0,998802
268 0,998479 309 0,998664 350 0,998805
269 0,998484 310 0,998668 351 0,998808
270 0,998489 311 0,998671 352 0,998811
271 0,998495 312 0,998675 353 0,998814
272 0,998500 313 0,998679 354 0,998817
273 0,998505 314 0,998683 355 0,998820
274 0,99851 315 0,998687 356 0,998823
275 0,998515 316 0,998690 357 0,998826
276 0,998519 317 0,998694 358 0,998829
277 0,998524 318 0,998698 359 0,998832
278 0,998529 319 0,998701 360 0,998835
279 0,998534 320 0,998705 361 0,998837
280 0,998539 321 0,998709 362 0,998840
281 0,998544 322 0,998712 363 0,998843
282 0,998548 323 0,998716 364 0,998846
k c4'(k) k c4'(k) k c4'(k)
365 0,998849 411 0,998963 457 0,999054
366 0,998851 412 0,998965 458 0,999056
367 0,998854 413 0,998967 459 0,999058
368 0,998857 414 0,998970 460 0,999060
369 0,998860 415 0,998972 461 0,999061
370 0,998862 416 0,998974 462 0,999063
371 0,998865 417 0,998976 463 0,999065
372 0,998868 418 0,998978 464 0,999067
373 0,998871 419 0,998980 465 0,999068
374 0,998873 420 0,998982 466 0,999070
375 0,998876 421 0,998985 467 0,999072
376 0,998879 422 0,998987 468 0,999073
377 0,998881 423 0,998989 469 0,999075
378 0,998884 424 0,998991 470 0,999077
379 0,998886 425 0,998993 471 0,999078
380 0,998889 426 0,998995 472 0,999080
381 0,998892 427 0,998997 473 0,999082
382 0,998894 428 0,998999 474 0,999084
383 0,998897 429 0,999001 475 0,999085
384 0,998899 430 0,999003 476 0,999087
385 0,998902 431 0,999005 477 0,999088
386 0,998904 432 0,999007 478 0,999090
387 0,998907 433 0,999009 479 0,999092
388 0,998909 434 0,999011 480 0,999093
389 0,998912 435 0,999013 481 0,999095
390 0,998914 436 0,999015 482 0,999097
391 0,998917 437 0,999017 483 0,999098
392 0,998919 438 0,999019 484 0,999100
393 0,998921 439 0,999021 485 0,999101
394 0,998924 440 0,999023 486 0,999103
395 0,998926 441 0,999025 487 0,999104
396 0,998929 442 0,999027 488 0,999106
397 0,998931 443 0,999028 489 0,999108
398 0,998933 444 0,999030 490 0,999109
399 0,998936 445 0,999032 491 0,999111
400 0,998938 446 0,999034 492 0,999112
401 0,998940 447 0,999036 493 0,999114
402 0,998943 448 0,999038 494 0,999115
403 0,998945 449 0,999040 495 0,999117
404 0,998947 450 0,999042 496 0,999118
405 0,998950 451 0,999043 497 0,999120
406 0,998952 452 0,999045 498 0,999121
407 0,998954 453 0,999047 499 0,999123
408 0,998956 454 0,999049 500 0,999124
409 0,998959 455 0,999051    
410 0,998961 456 0,999052    

Methoden und Formeln für Box-Cox

Box-Cox-Formel

Wenn Sie eine Box-Cox-Transformation ausführen, transformiert Minitab die ursprünglichen Datenwerte (Yi) entsprechend der folgenden Formel:

wobei λ den Parameter für die Transformation darstellt. Minitab erstellt dann eine Regelkarte der transformierten Datenwerte (Wi). Weitere Informationen dazu, wie Minitab den optimalen Wert für λ auswählt, finden Sie unter Methoden und Formeln für Box-Cox-Transformation.

Gängige λ-Werte

Die folgende Tabelle zeigt einige gängige λ-Werte und deren Transformationen.
λ Transformation
2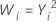
0,5
0
−0,5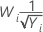
−1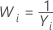
Copyright © 2024 Minitab, LLC. All rights Reserved.