Wählen Sie die gewünschte Methode oder Formel aus.
In diesem Thema
CUSUM-Plan, h, k und FIR
Bei beherrschten Prozessen eignen sich CUSUM-Karten gut zum Erkennen kleiner Shifts vom Sollwert, da sie Informationen zur Abfolge der Stichprobenwerte berücksichtigen. Die dargestellten Punkte sind die kumulierten Summen der Abweichungen der Stichprobenwerte vom Sollwert. Diese Punkte sollten eine zufällige Streuung um den Wert null aufweisen. Wenn sich ein Aufwärts- oder Abwärtstrend herausbildet, sollte dieser als Anzeichen für einen Shift des Prozessmittelwerts betrachtet werden, und Sie sollten nach Ausnahmebedingungen suchen.
- Tabellarische CUSUM (Standardeinstellung)
- Anhand der oberen CUSUM werden Shifts in der Prozesslage nach oben, anhand der unteren CUSUM Shifts nach unten erkannt. Die Regelkarte verwendet Eingriffsgrenzen (OEG und UEG), um zu ermitteln, ob ein Zustand aufgetreten ist, der nicht unter Kontrolle ist. Eine Erläuterung der tabellarischen CUSUMs finden Sie in Prins et al.1 sowie in Stoumbos et al.2.
- V-Masken-CUSUM
- Auf dieser Karte wird anstelle von Eingriffsgrenzen eine V-Maske verwendet, um zu bestimmen, ob eine Situation eingetreten ist, die nicht unter Kontrolle ist. Eine Erläuterung der V-Masken-Karte finden Sie in Lucas3 und Wadsworth et al.4.
CUSUM-Karten werden durch die beiden Parameter h und k definiert, die oft als CUSUM-Plan bezeichnet werden. Diese Werte werden häufig aus ARL-Tabellen (mittlere Reaktionsdauer) ausgewählt. Siehe Lucas3 und Lucas et al.5.
h
Bei tabellarischen CUSUMs ist h die Anzahl der Standardabweichungen zwischen der Mittellinie und den Eingriffsgrenzen. Dabei handelt es sich um den Wert, bei dem eine fehlende Kontrolle signalisiert wird.
Bei V-Masken-CUSUMs berechnet Minitab die halbe Breite der V-Maske (H) am Ursprungspunkt mit H = hσ.
Der Standardwert für h ist 4.
k
Bei tabellarischen CUSUMs ist k der zulässige „Schlupf“ im Prozess. In der CUSUM-Punktformel gibt k die Größe des Shifts an, die erkannt werden soll.
Bei V-Masken-CUSUMs ist k die Steigung der Schenkel der V-Maske. Sie können k mit Hilfe einer ARL-Tabelle auswählen.
Der Standardwert für k ist 0,5.
FIR
FIR (Fast Initial Response) ist eine Methode zum Initialisieren der tabellarischen CUSUM. Normalerweise werden tabellarische CUSUMs bei 0 initialisiert. Wenn ein Prozess jedoch von Beginn an nicht unter Kontrolle ist, wird die Situation von den CUSUMs einige Teilgruppen lang nicht erkannt.Tabellarische CUSUM
Dargestellte Punkte
Die auf einer CUSUM-Karte aufgetragenen Daten sind CUi, COi.
Wert einer unteren tabellarischen CUSUM zum Zeitpunkt i:

Dabei gilt Folgendes:
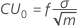
Wert einer oberen tabellarischen CUSUM zum Zeitpunkt i:
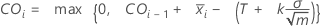
Dabei gilt Folgendes:
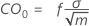
Mittellinie
Für die tabellarische Standard-CUSUM-Karte entspricht die Mittellinie 0.
Untere Eingriffsgrenze (UEG)
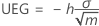
Obere Eingriffsgrenze (OEG)

Notation
| Begriff | Beschreibung |
|---|---|
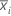 | Teilgruppenmittelwert |
| T | Sollwert |
| k | Größe des Shifts, der erkannt werden soll |
| σ | Standardabweichung des Prozesses |
| m | Teilgruppengröße |
| f | FIR |
| h | Entscheidungsintervall |
V-Masken-CUSUM
Dargestellte Punkte
Ci, der Wert einer V-Masken-CUSUM zum Zeitpunkt i =
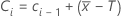
wobei C0 = 0
Steigung der V-Maske

Breite der V-Maske am Ursprung
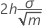
Ursprung der V-Maske
Für die Standardregelkarte wird n verwendet, um den Ursprung p zu schätzen.
Notation
| Begriff | Beschreibung |
|---|---|
| T | Sollwert |
| k | Steigung des Schenkels der V-Maske |
| h | Entscheidungsintervall |
| m | Teilgruppengröße |
Methoden und Formeln für Box-Cox
Box-Cox-Formel
Wenn Sie eine Box-Cox-Transformation ausführen, transformiert Minitab die ursprünglichen Datenwerte (Yi) entsprechend der folgenden Formel:


wobei λ den Parameter für die Transformation darstellt. Minitab erstellt dann eine Regelkarte der transformierten Datenwerte (Wi). Weitere Informationen dazu, wie Minitab den optimalen Wert für λ auswählt, finden Sie unter Methoden und Formeln für Box-Cox-Transformation.
Gängige λ-Werte
| λ | Transformation |
|---|---|
| 2 | 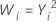 |
| 0,5 |  |
| 0 |  |
| −0,5 | 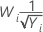 |
| −1 | 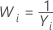 |
