Wählen Sie die gewünschte Methode oder Formel aus.
In diesem Thema
Dargestellte Punkte
Daten in Teilgruppen
Wenn sich die Daten in Teilgruppen befinden, wird T2 wie folgt berechnet:
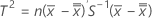
Dabei gilt Folgendes:
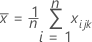
 ist der Mittelwertvektor von
ist der Mittelwertvektor von 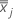 (Mittelwert von xjk-Werten ), die wie folgt berechnet wird:
(Mittelwert von xjk-Werten ), die wie folgt berechnet wird:
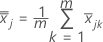
S = Kovarianzmatrix der Stichprobe
Die Kovarianzmatrix der Stichprobe S wird wie folgt berechnet:

Dabei gilt Folgendes:
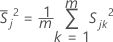
Dabei gilt Folgendes:
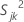 wird die Stichprobenvarianz für das j-te Merkmal in der k-ten Stichprobe wie folgt berechnet:
wird die Stichprobenvarianz für das j-te Merkmal in der k-ten Stichprobe wie folgt berechnet:
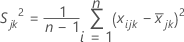
Dabei gilt Folgendes:
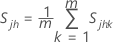
Dabei gilt Folgendes:
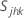 , die Kovarianz, =
, die Kovarianz, =
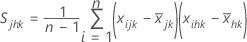
Der Durchschnitt der S-Matrizen ist ein erwartungstreuer Schätzwert der Varianz, wenn der Prozess beherrscht ist. n muss größer als p sein, und es dürfen keine starken Korrelationen zwischen den Variablen vorliegen, damit die Kovarianzmatrix der Stichprobe nicht singulär ist.
Wenn sich die Daten in Teilgruppen befinden, zeigt das Diagramm einen fehlenden Wert für jede Teilgruppe an, bei der es sich um eine einzelne Beobachtung handelt.
Einzelbeobachtungen
Wenn es sich bei den Daten um Einzelbeobachtungen handelt, wird T2 wie folgt berechnet:
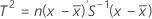
Dabei gilt Folgendes:
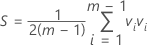
Dabei gilt Folgendes:

Notation
| Begriff | Beschreibung |
|---|---|
| n | Stichprobenumfang |
 | Vektor des Mittelwerts der Stichprobe |
| xijk | die i-ten Beobachtung des j-ten Merkmals in der k-ten Probe. |
| m | Anzahl der Stichproben |
Beispiel für das Berechnen des T2
Minitab stellt die T2-Statistik auf einer Regelkarte dar. Wenn ein dargestellter Punkt außerhalb der Eingriffsgrenzen liegt, ist der Prozess an dem betreffenden Punkt außer Kontrolle. Ziehen Sie die Tabelle und die Beispielgleichungen als Referenz für die Minitab-Berechnungen hinzu.
Die folgenden Daten stammen aus einem Entwicklungsprozess für eine Reinigungslösung. Die Anteile an Natriumcitrat und Glycerin wirken sich auf die Wirksamkeit der Lösung aus.
| Mittelwerte der Teilgruppen | Varianzen und Kovarianzen | T2-Statistik | ||||
| Teilgruppe | Natriumcitrat (X1) | Glycerin (X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| Durchschnitte | 7875 | 2333 | 7931 | 9318 | 3003 | |
- Berechnen Sie die Teilgruppenmittelwerte für jede Variable, X1 und X2. In diesem Fall enthielt jede Teilgruppe vier Stichproben.
- Wenn Einzelbeobachtungen erfasst wurden, verwendet Minitab diese anstelle der Teilgruppenmittelwerte in allen Berechnungen.
- Berechnen Sie die Varianzen der Teilgruppen, S1 2 und S2 2.
- Berechnen Sie die Kovarianzen der Teilgruppen, S1 2 k.
- Berechnen Sie die Mittelwerte der Teilgruppenmittelwerte, die Mittelwerte der Teilgruppenvarianzen und den Mittelwert der Kovarianzen.
- Legen Sie die Kovarianzmatrix der Stichprobe S und den mittleren Vektor fest.
- Berechnen Sie T2, das angegeben wird durch:
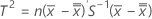
Minitab stellt T2 auf der T2-Karte dar und vergleicht den Wert mit den Eingriffsgrenzen, um festzustellen, ob einzelne Punkte außer Kontrolle sind.
Mittellinie
Die Mittellinie für die T2-Karte liegt bei KX. Die Berechnung von K und X hängt vom maximalen Stichprobenumfang und davon ab, ob Minitab die Kovarianzmatrix aus den Daten schätzt.
Daten in Teilgruppen
Wenn die Daten in Teilgruppen erfasst wurden, wird KX wie folgt berechnet:
- Gegebene Kovarianzmatrix
-


- Geschätzte Kovarianzmatrix
-


Einzelbeobachtungen
Wenn die Daten als Einzelbeobachtungen erfasst wurden, wird KX wie folgt berechnet:
- Gegebene Kovarianzmatrix
-
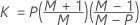
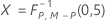
- Geschätzte Kovarianzmatrix
-
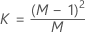
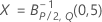
Dabei gilt Folgendes:
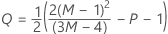
Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Variablen |
| M | Anzahl der Teilgruppen |
| N | Stichprobenumfang |
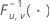 | inverse kumulative F-Verteilung mit u Freiheitsgraden des Zählers und v Freiheitsgraden des Nenners |
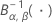 | inverse kumulative Betaverteilung mit dem ersten Formparameter α und dem zweiten Formparameter β |
Eingriffsgrenze
Daten in Teilgruppen
Die obere Eingriffsgrenze wird wie folgt ausgedrückt, wenn Sie keine Parameter angeben:
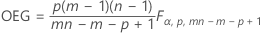
Die obere Eingriffsgrenze wird wie folgt ausgedrückt, wenn Sie Parameter angeben:
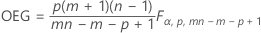
Einzelbeobachtungen
Die obere Eingriffsgrenze wird wie folgt ausgedrückt, wenn Sie keine Parameter angeben:
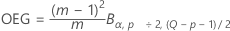
Dabei gilt Folgendes:
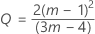
Weitere Informationen finden Sie in Woodall et al.1
Die obere Eingriffsgrenze wird wie folgt ausgedrückt, wenn Sie Parameter angeben:
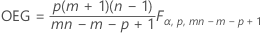
Notation
| Begriff | Beschreibung |
|---|---|
| α | fester Wert von 0,00134989803156746 |
| p | Anzahl der Merkmale |
| m |
Wenn Sie für Daten in Teilgruppen keine Parameterschätzwerte angeben, ist m gleich der Anzahl der Stichproben. Wenn Sie Parameterschätzwerte angeben, entspricht m der Anzahl der Stichproben, mit denen die Kovarianzmatrix erstellt wird. Für Einzelwerte ist m die Anzahl der Beobachtungen. |
| n | Umfang der einzelnen Stichproben |
| F | Angabe, dass die F-Verteilung verwendet wird |
| B | Angabe, dass die Betaverteilung verwendet wird |
Zerlegte T2-Statistik
Zerlegte T2-Statistik:
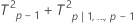
Dabei gilt Folgendes:

Dabei gilt Folgendes:
xi(p − 1) ist der zerlegte mittlere Vektor
Sxx ist die (p – 1) × (p – 1)-Haupt-Teilmatrix von S
T2p|1,..., p−1 ist eine Approximation, die sich entsprechend den Phasen und dem Vorhandensein von Teilgruppen oder Einzelbeobachtungen unterscheidet:
Phase 1 für Daten in Teilgruppen:
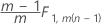
Phase 2 für Daten in Teilgruppen:
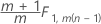
Phase 1 für Einzelbeobachtungen:
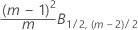
Phase 2 für Einzelbeobachtungen:
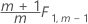
Minitab berechnet die Eingriffsgrenzen für Phase 1, wenn Sie keine Parameterschätzwerte angeben, und für Phase 2, wenn Sie Parameterschätzwerte angeben.
In Mason et al.2 finden Sie weitere Informationen zur zerlegten T2-Statistik.
Notation
| Begriff | Beschreibung |
|---|---|
| m | Anzahl der Stichproben |
| F | Angabe, dass die F-Verteilung verwendet wird |
| B | Angabe, dass die Betaverteilung verwendet wird |
Methoden und Formeln für Box-Cox
Box-Cox-Formel
Wenn Sie eine Box-Cox-Transformation ausführen, transformiert Minitab die ursprünglichen Datenwerte (Yi) entsprechend der folgenden Formel:


wobei λ den Parameter für die Transformation darstellt. Minitab erstellt dann eine Regelkarte der transformierten Datenwerte (Wi). Weitere Informationen dazu, wie Minitab den optimalen Wert für λ auswählt, finden Sie unter Methoden und Formeln für Box-Cox-Transformation.
Gängige λ-Werte
| λ | Transformation |
|---|---|
| 2 | 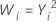 |
| 0,5 |  |
| 0 |  |
| −0,5 | 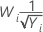 |
| −1 | 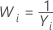 |
