In diesem Thema
Dargestellte Punkte
Die dargestellten Punkte auf der T2-Karte sind die T2-Werte für jede Teilgruppe.
Interpretation
Wenn der Prozess beherrscht ist, liegen die Punkte unter der oberen Eingriffsgrenze, und der Prozess weist lediglich Streuung durch gewöhnliche Ursachen auf. Untersuchen Sie alle Punkte, die über der oberen Eingriffsgrenze liegen. Ein Nachteil von multivariaten Regelkarten besteht darin, dass die Skala in keiner Beziehung zu den Skalen der Variablen steht und aus den Signalen fehlender Kontrolle nicht hervorgeht, welche Variable (bzw. Kombination von Variablen) das jeweilige jeweilige Signal bewirkt hat.
Mittellinie
Die Mittellinie ist der Median der theoretischen Verteilung der T2-Statistik.
Interpretation
Anhand der Mittellinie können Sie die Leistung des Prozesses verglichen mit dem Durchschnitt untersuchen. Wenn der Prozess beherrscht ist, liegen die Punkte in zufälliger Verteilung um die Mittellinie.
Eingriffsgrenzen
Die obere Eingriffsgrenze ist die horizontale Linie oberhalb der Mittellinie. Die obere Eingriffsgrenze veranschaulicht, ob ein Prozess außer Kontrolle ist, und sie basiert auf der beobachteten Streuung innerhalb der Teilgruppen und der erwarteten Streuung der dargestellten Punkte.
Zerlegte T2-Werte
Die zerlegten T2-Werte geben den individuellen Beitrag jeder Variablen für alle Punkte außer Kontrolle auf einer T2-Karte an.
Einzelne Datenpunkte in einer T2-Karte sind zusammengesetzte Werte, die mehrere Variablen darstellen. Damit wird aus einer T2-Karte nicht ersichtlich, wie viel die einzelnen Variablen jeweils zu einem kombinierten Punktwert beitragen, was die Interpretation der Punkte außer Kontrolle erschwert. Wenn ein Punkt auf einer T2-Karte außer Kontrolle ist, können Sie nicht feststellen, ob die fehlende Kontrolle auf alle Variablen, einige Variablen oder nur eine Variable zurückzuführen ist. Die zerlegten T2-Werte geben jedoch Aufschluss darüber, ob eine Variable stärker als die übrigen Variablen zur fehlenden Kontrolle beiträgt.
Kovarianzmatrizen
Eine Kovarianzmatrix ist eine quadratische Matrix, die die Varianzen und Kovarianzen für mehrere Variablen enthält. Die diagonalen Elemente der Matrix enthalten die Varianzen der Variablen, die nicht diagonalen Elemente enthalten die Kovarianzen zwischen allen möglichen Paaren von Variablen.
Die Varianz-Kovarianz-Matrix ist symmetrisch, da die Kovarianz zwischen x und y gleich der Kovarianz zwischen y und x ist. Daher ist die Kovarianz für jedes Paar von Variablen zweimal in der Matrix zu finden: Die Kovarianz zwischen der i-ten und der j-ten Variablen wird an den Positionen (i, j) und (j, i) angezeigt.
Nachdem Sie die Kovarianzmatrizen gespeichert haben, wählen Sie aus, um die Kovarianzmatrizen anzuzeigen.
Interpretation
| X | Y | Z | |
| X | 2,0 | −0,86 | −0,15 |
| Y | −0,86 | 3,4 | 0,48 |
| Z | −0,15 | 0,48 | 0,82 |
Die Varianzen werden fett formatiert entlang der Diagonalen angezeigt. Die Varianzen von X, Y und Z sind 2,0, 3,4 und 0,82. Die Kovarianz zwischen X und Y ist −0,86, die Kovarianz zwischen X und Z ist −0,15, und die Kovarianz zwischen Y und Z ist 0,48.
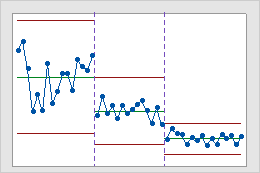
Abschnitte
Verwenden Sie Abschnitte, um eine historische Regelkarte zu erstellen, mit der die Änderung eines Prozesses über bestimmte Zeiträume veranschaulicht wird. In der Standardeinstellung berechnet Minitab die Mittellinie und die Eingriffsgrenzen für jeden Abschnitt neu. Weitere Informationen finden Sie unter Hinzufügen von Abschnitten zum Darstellen der Änderungen eines Prozesses.
Interpretation
Diese historische Regelkarte zeigt drei Abschnitte eines Prozesses, die für die Zeiträume vor, während und nach der Umsetzung eines neuen Verfahrens stehen.