In diesem Thema
Dargestellte Punkte
Jeder Punkt auf einer p'-Karte nach Laney stellt den Anteil fehlerhafter Einheiten für eine Teilgruppe dar.
Interpretation
Wenn der Prozess beherrscht ist, liegen die Punkte in zufälliger Verteilung um die Mittellinie, und der Prozess weist lediglich Streuung durch gewöhnliche Ursachen auf. Untersuchen Sie Punkte außerhalb der Eingriffsgrenzen sowie Punkte, die nicht zufälligen Mustern folgen, auf mögliche Streuung durch Ausnahmebedingungen.
Mittellinie
Die Mittellinie auf einer p'-Karte nach Laney stellt den durchschnittlichen Anteil fehlerhafter Einheiten für den Prozess dar. Der durchschnittliche Anteil fehlerhafter Einheiten wird auch als Prozessanteil bezeichnet.
Interpretation
Anhand der Mittellinie können Sie die Leistung des Prozesses verglichen mit dem Durchschnitt untersuchen. Wenn der Prozess beherrscht ist, liegen die Punkte in zufälliger Verteilung um die Mittellinie.
Achtung
Verwechseln Sie die Mittellinie nicht mit dem Sollwert des Prozesses. Der Sollwert ist das gewünschte Ergebnis. Die Mittellinie hingegen gibt das tatsächliche Ergebnis an.
Eingriffsgrenzen
Achtung
Eingriffsgrenzen dürfen nicht mit Spezifikationsgrenzen verwechselt werden. Spezifikationsgrenzen stellen normalerweise Kundenanforderungen dar und geben den gewünschten Betrag der Streuung im Prozess an. Eingriffsgrenzen geben den tatsächlichen Betrag der Streuung gemäß den Stichprobendaten an. Ein Prozess kann beherrscht sein und dennoch nicht die Spezifikationen erfüllen.
Sigma-Z
Sigma-Z ist ein Maß der Überdispersion oder Unterdispersion in den Daten.
Interpretation
- Ein Sigma-Z-Wert von 1 gibt an, dass keine Korrektur erforderlich ist. In diesem Fall sind die Eingriffsgrenzen auf der p'-Karte nach Laney identisch mit den Eingriffsgrenzen auf einer herkömmlichen p-Karte.
- Ein Sigma-Z-Wert größer als 1 weist darauf hin, dass die Eingriffsgrenzen auf der p'-Karte nach Laney breiter als die Eingriffsgrenzen auf einer herkömmlichen p-Karte sind, um eine Überdispersion auszugleichen.
- Ein Sigma-Z-Wert kleiner als 1 weist darauf hin, dass die Eingriffsgrenzen auf der p'-Karte nach Laney enger als die Eingriffsgrenzen auf einer herkömmlichen p-Karte sind, um eine Unterdispersion auszugleichen.
Die folgenden Grafiken zeigen beispielsweise eine herkömmliche p-Karte und eine p'-Karte nach Laney derselben Daten. Die Teilgruppen sind groß, und die Daten weisen eine Überdispersion auf.
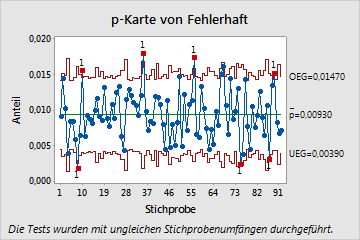
- Herkömmliche p-Karte
- Auf der herkömmlichen p-Karte führen die großen Teilgruppengrößen zu engen Eingriffsgrenzen. Die engen Eingriffsgrenzen und die Überdispersion führen dazu, dass mehrere Teilgruppen anscheinend außer Kontrolle sind.
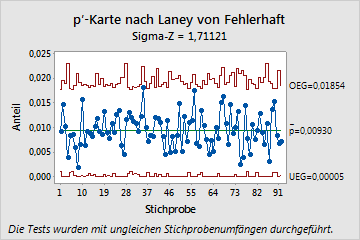
- p'-Karte nach Laney
- Die Eingriffsgrenzen auf der p'-Karte nach Laney werden zum Ausgleichen der Überdispersion korrigiert. Die p'-Karte nach Laney zeigt, dass der Prozess tatsächlich beherrscht ist. Keine Punkte liegen außerhalb der Eingriffsgrenzen.
Tests auf Ausnahmebedingungen
Mit den Tests auf Ausnahmebedingungen wird untersucht, ob die dargestellten Punkte zufällig innerhalb der Eingriffsgrenzen verteilt sind.
Interpretation
Bestimmen Sie mit Hilfe von Tests auf Ausnahmebedingungen, welche Beobachtungen möglicherweise untersucht werden müssen, und ermitteln Sie bestimmte Muster und Trends in Ihren Daten. Mit jedem der Tests auf Ausnahmebedingungen wird ein bestimmtes Muster oder ein bestimmter Trend in den Daten erkannt, das bzw. der einen jeweils anderen Aspekt der Prozessinstabilität aufdeckt. Mit Test 1 wird beispielsweise ein einzelner Punkt erkannt, der nicht unter Kontrolle ist. Mit Test 2 wird ein möglicher Shift im Prozess erkannt.
Für diese Regelkarte sind vier Tests verfügbar.
- Test 1: 1 Punkt mehr als 3 σ von der Mittellinie
- Mit Test 1 werden Teilgruppen erkannt, die im Vergleich mit anderen Teilgruppen ungewöhnlich sind. Test 1 ist allgemein als notwendig zum Erkennen einer fehlenden Kontrolle anerkannt. Wenn kleine Shifts im Prozess von Interesse sind, kann Test 1 durch Test 2 ergänzt werden, um die Empfindlichkeit der Regelkarte zu steigern.
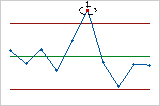
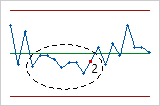
- Test 2: 9 aufeinander folgende Punkte auf der gleichen Seite der Mittellinie
- Mit Test 2 werden Shifts im Anteil fehlerhafter Einheiten für den Prozess erkannt. Wenn kleine Shifts im Prozess von Interesse sind, kann Test 1 durch Test 2 ergänzt werden, um die Empfindlichkeit der Regelkarte zu steigern.
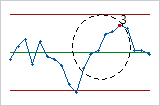
- Test 3: 6 aufeinander folgende Punkte, alle zu- oder abnehmend
- Mit Test 3 werden Trends erkannt. Bei diesem Test wird nach langen Reihen aufeinander folgender Punkte gesucht, deren Wert durchgängig zu- oder abnimmt.
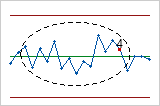
- Test 4: 14 aufeinander folgende Punkte, abwechselnd auf- und abwärts
- Mit Test 4 wird systematische Streuung erkannt. Das Muster der Streuung in einem Prozess soll zufällig sein; ein Punkt, der Test 4 nicht besteht, kann jedoch u. U. darauf hinweisen, dass das Streuungsmuster prognostizierbar ist.
Abschnitte
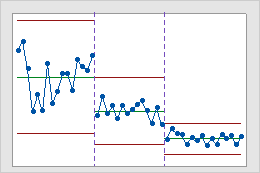
Verwenden Sie Abschnitte, um eine historische Regelkarte zu erstellen, mit der die Änderung eines Prozesses über bestimmte Zeiträume veranschaulicht wird. In der Standardeinstellung berechnet Minitab die Mittellinie und die Eingriffsgrenzen für jeden Abschnitt neu. Weitere Informationen finden Sie unter Hinzufügen von Abschnitten zum Darstellen der Änderungen eines Prozesses.
Interpretation
Diese historische Regelkarte zeigt drei Abschnitte eines Prozesses, die für die Zeiträume vor, während und nach der Umsetzung eines neuen Verfahrens stehen.