Prozessfähigkeitsindizes für mit Johnson-Transformation transformierte Daten
Bei der Johnson-Transformation wird die optimale Funktion aus drei Familien von Verteilungen einer Variablen ausgewählt, die einfach in eine Standardnormalverteilung transformiert werden können. Diese Verteilungen werden mit SB, SL und SU gekennzeichnet, wobei sich B, L und U auf eine beschränkte, lognormale oder unbeschränkte Variable beziehen. In Minitab werden die Parameter für die Verteilungen als erste Form, zweite Form, Lage und Skala bezeichnet. Weitere Informationen finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung; klicken Sie dort auf „Methoden und Formeln für die Johnson-Transformation“.
Wenn beide Spezifikationsgrenzen innerhalb der Spannweite der Transformationsfunktion liegen, berechnet Minitab die Indizes der Gesamtprozessfähigkeit auf der Grundlage der Normalverteilung für die transformierten Daten. Weitere Informationen finden Sie unter Methoden und Formeln für Maße der Gesamtprozessfähigkeit in Prozessfähigkeitsanalyse für Normalverteilung.
Wenn es sich bei der ausgewählten Familie um den Typ SB oder SL handelt und die untere und/oder obere Spezifikationsgrenze außerhalb der Spannweite der Verteilung liegt, führt Minitab zusätzliche Berechnungen durch, um die Indizes der Gesamtprozessfähigkeit zu bestimmen.
SB-Verteilung
Wenn mindestens eine der Spezifikationsgrenzen (X) vor der Transformation außerhalb der Spannweite der Verteilung liegt (nicht ε < X < ε + λ), werden Pp, Ppk, PPL, PPU, Z.USG und Z.OSG wie folgt berechnet:
Zuerst berechnet Minitab die Perzentile im transformierten Raum.
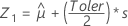
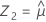

Anhand der drei z-Werte berechnet Minitab die entsprechenden Werte für X1, X2 und X3 im ursprünglichen Raum:
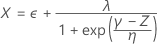
Die Indizes für die Gesamtprozessfähigkeit werden dann aus den X-Werten und den Werten der Spezifikationsgrenzen berechnet.
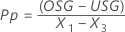


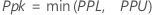


Notation
| Term | Description |
|---|---|
| USG | Untere Spezifikationsgrenze |
| OSG | Obere Spezifikationsgrenze |
 | Mittelwert der Stichprobe (X̅) der transformierten Daten |
| Toler | Toleranz bei Standardabweichungen |
| s | Standardabweichung der Stichprobe der transformierten Daten |
| ε, | Lageparameter der Johnson-Transformation |
| γ | Formparameter der Johnson-Transformation |
| η | Formparameter der Johnson-Transformation (η > 0) |
| λ | Skalenparameter der Johnson-Transformation (λ > 0) |
Die Berechnungen für Z.Bench und die Werte der erwarteten Leistung für eine SB-Verteilung hängen von der Lage der USG und der OSG im Verhältnis zu X2 sowie von den Verteilungsgrenzen ab.
- Die USG und die OSG befinden sich auf entgegengesetzten Seiten von X2
-
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
Z.Bench fehlt
PPM < USG = 0
PPM > OSG = 0
PPM Gesamt = 0
- Wenn eine Spezifikationsgrenze außerhalb und die andere innerhalb der Spannweite der Verteilung liegt, berechnet Minitab die folgenden Werte:

PPM für Spezifikationsgrenze außerhalb der Spannweite = 0
PPM für Spezifikationsgrenze innerhalb der Spannweite = p*1000000
PPM Gesamt = p*1000000
Note
Minitab verwendet die transformierten Daten und die transformierten Spezifikationsgrenzen, um PPM zu berechnen.
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
- Die USG und die OSG befinden sich links von X2
-
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
Z.Bench fehlt
PPM < USG = 0
PPM > OSG = 1
PPM Gesamt = 1
- Wenn die USG außerhalb und die OSG innerhalb der Spannweite der Verteilung liegt, berechnet Minitab die folgenden Werte:

PPM < USG = 0
PPM > OSG = p*1000000
PPM Gesamt = PPM > OSG
Note
Minitab verwendet die transformierten Daten und die transformierten Spezifikationsgrenzen, um PPM zu berechnen.
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
- Die USG und die OSG befinden sich rechts von X2
-
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
Z.Bench fehlt
PPM < USG = 1
PPM > OSG = 0
PPM Gesamt = 1
- Wenn die USG innerhalb und die OSG außerhalb der Spannweite der Verteilung liegt, berechnet Minitab die folgenden Werte:

PPM < USG = p*1000000
PPM > OSG = 0
PPM Gesamt = PPM < USG
Note
Minitab verwendet die transformierten Daten und die transformierten Spezifikationsgrenzen, um PPM zu berechnen.
- Wenn sowohl die USG als auch die OSG außerhalb der Spannweite der Verteilung liegen, zeigt Minitab Folgendes an:
SL-Verteilung
Wenn mindestens eine der Spezifikationsgrenzen vor der Transformation außerhalb der Spannweite der Verteilung liegt, verwendet Minitab zur Berechnung von Pp, Ppk, PPL, PPU, Z.USG und Z.OSG dieselbe Methode, die oben für die SB-Verteilung dargestellt ist. Die einzige Abweichung besteht in der Formel zum Ermitteln des Originalwerts von X aus dem transformierten Wert Z.

- USG und OSG sind kleiner oder gleich ε (beide liegen außerhalb der Spannweite der Verteilung)
-
Z.Bench fehlt
PPM < USG = 0
PPM > OSG = 1
PPM Gesamt = 1
- USG ist kleiner oder gleich ε
-

PPM < USG = 0
PPM > OSG = p*1000000
PPM Gesamt = PPM > OSG
Notation
| Term | Description |
|---|---|
 | Inverse kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
| p | Wahrscheinlichkeit, mit der die transformierten Daten außerhalb der transformierten Spezifikationsgrenze liegen |
