Support für Minitab® 

Auswählen der Verteilung und Eingeben der Parameter

Weitere Informationen zu Minitab
Wählen Sie Berechnen > Zufallszahlen aus, wählen Sie die Verteilung aus, und geben Sie die Parameter ein.

In diesem Thema

Bernoulli

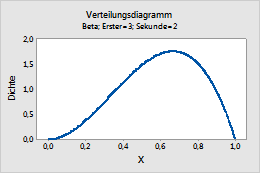
Geben Sie im Feld Ereigniswahrscheinlichkeit eine Zahl zwischen 0 und 1 für die Wahrscheinlichkeit ein, mit der das Ereignis von Interesse auftritt. Ein Vorkommen wird als „Ereignis“ bezeichnet. Weitere Informationen finden Sie unter Bernoulli-Verteilung.
Verwenden Sie die Bernoulli-Verteilung, wenn ein zufälliger Prozess genau zwei Ergebnisse hat: Ereignis oder Nicht-Ereignis. Folgen unabhängiger Bernoulli-Versuche erzeugen die anderen Verteilungen, z. B. die Binomialverteilung, die die Anzahl der Erfolge in n Versuchen modelliert. Dieses Diagramm zeigt beispielsweise eine Zufallsstichprobe aus einer Binomialverteilung mit 1 Versuch und einer Ereigniswahrscheinlichkeit von 0,15.

Beta

Führen Sie die folgenden Schritte aus, um die Parameter für die Betaverteilung einzugeben.

  1. Geben Sie im Feld Erster Formparameter eine Zahl größer als null für den ersten Formparameter ein.
  2. Geben Sie im Feld Zweiter Formparameter eine Zahl größer als null für den zweiten Formparameter ein.

Dieses Diagramm stellt beispielsweise eine Betaverteilung mit einer ersten Form von 3 und einer zweiten Form von 2 dar.

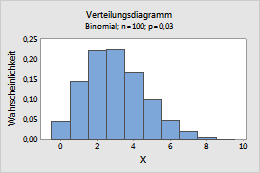
Binomial

Führen Sie die folgenden Schritte aus, um die Parameter für die Binomialverteilung einzugeben.

  1. Geben Sie im Feld Anzahl der Versuche den Stichprobenumfang ein.
  2. Geben Sie im Feld Ereigniswahrscheinlichkeit eine Zahl zwischen 0 und 1 für die Wahrscheinlichkeit ein, mit der das Ereignis von Interesse auftritt. Ein Vorkommen wird als „Ereignis“ bezeichnet.

Dieses Diagramm stellt beispielsweise eine Binomialverteilung mit 100 Versuchen und einer Ereigniswahrscheinlichkeit von 0,03 dar.

Cauchy

Führen Sie die folgenden Schritte aus, um die Parameter für die Cauchy-Verteilung einzugeben.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Verteilungsspitze darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der Verteilung darstellt.

Dieses Diagramm stellt beispielsweise eine Cauchy-Verteilung mit der Lage 0 und der Skala 1 dar.

Chi-Quadrat

Geben Sie im Feld Freiheitsgrade die Anzahl der Freiheitsgrade ein, die die Chi-Quadrat-Verteilung definieren.

Dieses Diagramm stellt z. B. eine Chi-Quadrat-Verteilung mit 4 Freiheitsgraden dar.

Diskret

Führen Sie die folgenden Schritte aus, um die Parameter für die Diskrete Verteilung einzugeben.

  1. Geben Sie im Feld Werte in die Spalte mit den Werten ein, die in die Verteilung eingebunden werden sollen. In der Regel handelt es sich bei den Werten um diskrete Ereignisse oder Zählungen, die durch numerische Werte dargestellt werden.
  2. Geben Sie im Feld Wahrscheinlichkeiten in die Spalte ein, die die Wahrscheinlichkeiten für die einzelnen Werte enthält. Die Wahrscheinlichkeiten müssen zwischen 0 und 1 liegen und in der Summe 1 ergeben.

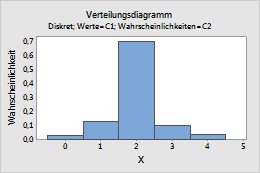
In diesem Arbeitsblatt enthält Wert die in die Verteilung einzubindenden Anzahlen und Wahrscheinlichkeit die Wahrscheinlichkeit der einzelnen Anzahlen.

C1 C2
Wert Wahrscheinlichkeit
0 0,03
1 0,13
2 0,70
3 0,10
4 0,04

Exponential

Führen Sie die folgenden Schritte aus, um Parameter für die Exponentialverteilung einzugeben.

  1. Geben Sie im Feld Skala den Skalenparameter ein. Der Skalenparameter ist gleich dem Mittelwert, wenn der Schwellenwertparameter gleich 0 ist.
  2. Geben Sie im Feld Schwellenwert die Untergrenze der Verteilung ein.

Dieses Diagramm stellt beispielsweise eine Exponentialverteilung mit der Skala 1 und dem Schwellenwert 0 dar.

F

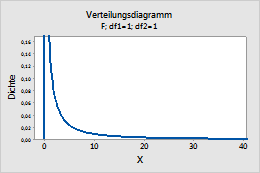
Geben Sie im Feld Freiheitsgrade des Zählers und im Feld Freiheitsgrade des Nenners die Freiheitsgrade des Zählers und des Nenners ein, mit denen die F-Verteilung definiert werden soll. Weitere Informationen finden Sie unter F-Verteilung.

Dieses Diagramm stellt z. B. eine F-Verteilung mit 1 Freiheitsgrad des Zählers und 1 Freiheitsgrad des Nenners dar.

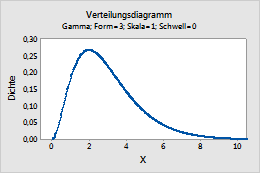
Gamma

Führen Sie die folgenden Schritte aus, um die Parameter für die Gamma-Verteilung einzugeben.

  1. Geben Sie im Feld Formparameter einen Wert ein, der die Form der Verteilung darstellt.
  2. Geben Sie im Feld Skalenparameter einen Wert ein, der die Skala der Verteilung darstellt.
  3. Geben Sie im Feld Schwellenwertparameter die Untergrenze der Verteilung ein.

Dieses Diagramm stellt beispielsweise eine Gamma-Verteilung mit der Form 3, der Skala 1 und dem Schwellenwert 0 dar.

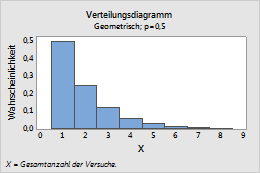
Geometrisch

Führen Sie die folgenden Schritte aus, um Parameter für die Geometrische Verteilung einzugeben.

  1. Geben Sie im Feld Ereigniswahrscheinlichkeit eine Zahl zwischen 0 und 1 für die Wahrscheinlichkeit des Vorkommens in jedem Versuch ein. Ein Vorkommen wird als „Ereignis“ bezeichnet.
  2. Um anzugeben, welche Version der geometrischen Verteilung Sie verwenden möchten, klicken Sie auf Optionen, und wählen Sie eine der folgenden Optionen aus:
    • Gesamtanzahl der Versuche modellieren: Es wird die Gesamtanzahl der zum Auslösen eines einzelnen Ereignisses benötigten Versuche modelliert.
    • Nur die Anzahl der Nicht-Ereignisse modellieren: Es wird die Anzahl der Nicht-Ereignisse modelliert, die vor dem ersten Ereignis eintreten.
    Tipp

    Um die Standardeinstellungen für künftige Minitab-Sessions zu ändern, wählen Sie Datei > Optionen > Einzelne Befehle > Verteilungen aus.

Dieses Diagramm stellt beispielsweise eine geometrische Verteilung dar, die die Gesamtzahl der Versuche modelliert und eine Ereigniswahrscheinlichkeit von 0,5 aufweist.

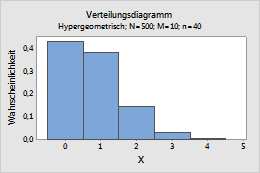
Hypergeometrisch

Führen Sie die folgenden Schritte aus, um die Parameter für die Hypergeometrische Verteilung einzugeben.

  1. Geben Sie im Feld Größe der Grundgesamtheit (N) die Gesamtanzahl der Einheiten in der Grundgesamtheit (N) an. Wenn N zu groß ist, um bekannt zu sein, nähert sich die Binomialverteilung der hypergeometrischen Verteilung an.
  2. Geben Sie im Feld Ereigniszahl in Grundgesamtheit (M) eine Zahl zwischen 0 und N (Größe der Grundgesamtheit) ein, um die Anzahl der Ereignisse in der Grundgesamtheit anzugeben.
  3. Geben Sie im Feld Stichprobenumfang (n) die Anzahl der Einheiten an, die ohne Zurücklegen als Stichprobe gezogen werden.

Dieses Diagramm stellt beispielsweise eine hypergeometrische Verteilung mit der Grundgesamtheit 400, der Ereigniszahl 10 und der Stichprobengröße 40 dar.

Ganzzahlig

Führen Sie die folgenden Schritte aus, um die Parameter für die Ganzzahlige Verteilung einzugeben.

  1. Geben Sie im Feld Minimum den unteren Endpunkt der Verteilung ein.
  2. Geben Sie im Feld Maximum den oberen Endpunkt der Verteilung ein.

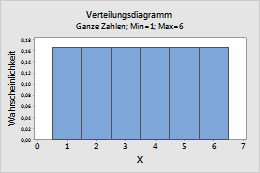
Dieses Diagramm stellt beispielsweise eine ganzzahlige Verteilung mit einem Minimum von 1 und einem Maximum von 6 dar.

Laplace

Führen Sie die folgenden Schritte aus, um die Parameter für die Laplace-Verteilung einzugeben.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Verteilungsspitze darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der Verteilung darstellt.

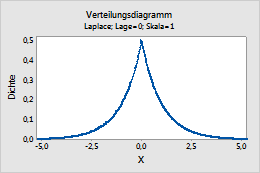
Dieses Diagramm stellt beispielsweise eine Laplace-Verteilung mit der Lage 0 und der Skala 1 dar.

Größter Extremwert

Führen Sie die folgenden Schritte aus, um die Parameter für die Verteilung des größten Extremwerts einzugeben. Weitere Informationen finden Sie unter Verteilung des größten und des kleinsten Extremwerts.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Verteilungsspitze darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der Verteilung darstellt.

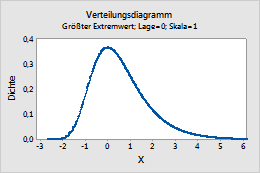
Dieses Diagramm stellt beispielsweise eine Verteilung des größten Extremwerts mit der Lage 0 und der Skala 1 dar.

Logistisch

Führen Sie die folgenden Schritte aus, um die Parameter für die Logistische Verteilung einzugeben.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Verteilungsspitze darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der Verteilung darstellt.

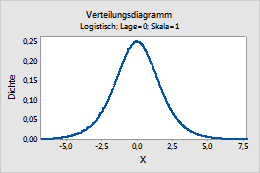
Dieses Diagramm stellt beispielsweise eine logistische Verteilung mit der Lage 0 und der Skala 1 dar.

Loglogistisch

Führen Sie die folgenden Schritte aus, um Parameter für die Loglogistische Verteilung einzugeben.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Spitze der entsprechenden logistischen Verteilung darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der entsprechenden logistischen Verteilung darstellt.
  3. Geben Sie im Feld Schwellenwert die Untergrenze der Verteilung ein.

Dieses Diagramm stellt beispielsweise eine loglogistische Verteilung mit der Lage 0, der Skala 1 und dem Schwellenwert 0 dar.

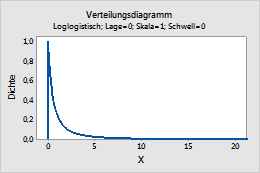
Lognormal

Führen Sie die folgenden Schritte aus, um Parameter für die Lognormale Verteilung einzugeben.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Spitze der entsprechenden Normalverteilung darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der entsprechenden Normalverteilung darstellt.
  3. Geben Sie im Feld Schwellenwert die Untergrenze der Verteilung ein.

Dieses Diagramm stellt beispielsweise eine lognormale Verteilung mit der Lage 0, der Skala 1 und dem Schwellenwert 0 dar.

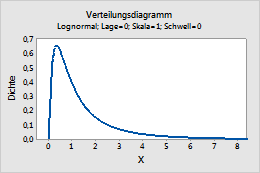
Multivariat normal

Führen Sie die folgenden Schritte aus, um Parameter für die Multivariate Normalverteilung einzugeben.

  1. Geben Sie im Feld Mittelwertspalte die Spalte ein, die den Vektor des Mittelwerts enthält.
  2. Geben Sie im Feld Varianz-Kovarianz-Matrix die Matrix (z. B. M1) ein, die die Varianzen und Kovarianzen der Variablen in derselben Reihenfolge wie die Mittelwertspalte enthält.

In diesem Beispiel stammen die Daten aus drei korrelierenden, normalverteilten, zufälligen Variablen. Die Mittelwerte befinden sich in der Spalte C1, und die Varianz-Kovarianz-Matrix ist in den Spalten C2–C4.

C1 C2 C3 C4
       
2,0 13,0321 2,6544 0,0899
100,1 2,6544 6,5883 1,4438
151,3 0,0899 1,4438 12,2219

Zuerst muss Minitab die Varianz-Kovarianz-Matrix einlesen und speichern.
  1. Wählen Sie Daten > Kopieren > Spalten in Matrix aus.
  2. Geben Sie im Feld Aus Spalten kopieren die Spalten C2-C4 ein.
  3. Geben Sie im Feld Kopierte Daten speichern unter In aktuellem Arbeitsblatt, in Matrix: die Matrix M1 ein.
  4. Klicken Sie auf OK.

Jetzt können Sie Zufallszahlen aus der multivariaten Normalverteilung generieren.

  1. Wählen Sie Berechnen > Zufallszahlen > Multivariat normal aus.
  2. Geben Sie im Feld Anzahl der zu generierenden Datenzeilen die gewünschte Anzahl Zeilen ein. Geben Sie für dieses Beispiel 18 ein.
  3. Geben Sie im Feld In Spalte(n) speichern Ihre Speicherspalten ein. Geben Sie für dieses Beispiel C6-C8 ein.
  4. Geben Sie im Feld Mittelwertspalte die Spalte ein, die den Mittelwert enthält. Geben Sie für dieses Beispiel C1 ein.
  5. Geben Sie im Feld Varianz-Kovarianz-Matrix die Matrix ein. Geben Sie für dieses Beispiel M1 ein.
  6. Klicken Sie auf OK.
Tipp

Um dieselbe Stichprobe zu erhalten wie in der Tabelle unten, legen Sie die Basis des Zufallszahlengenerators fest, bevor Sie die Zufallsstichprobe erzeugen. Wählen Sie Berechnen > Basis festlegen aus, und geben Sie 5 ein.

C6 C7 C8
     
1,61033 99,192 148,814
0,45883 96,093 144,679
−0,46745 101,041 148,936
… … …

Negativ binomial

Führen Sie die folgenden Schritte aus, um Parameter für die Negative Binomialverteilung einzugeben.

  1. Geben Sie im Feld Ereigniswahrscheinlichkeit eine Zahl zwischen 0 und 1 für die Wahrscheinlichkeit des Vorkommens in jedem Versuch ein. Ein Vorkommen wird als „Ereignis“ bezeichnet.
  2. Geben Sie im Feld Erforderliche Anzahl der Ereignisse eine positive ganze Zahl ein, die angibt, wie häufig das Ereignis eintreten muss.
  3. Um anzugeben, welche Version der negativen Binomialverteilung Sie verwenden möchten, klicken Sie auf Optionen, und wählen Sie eine der folgenden Optionen aus:
    • Gesamtanzahl der Versuche modellieren: Es wird die Gesamtanzahl der zum Auslösen der angegebenen Anzahl von Ereignissen benötigten Versuche modelliert.
    • Nur die Anzahl der Nicht-Ereignisse modellieren: Es wird die Anzahl der Nicht-Ereignisse modelliert, die vor dem Eintreten einer angegebenen Anzahl von Ergebnissen eintreten.
    Tipp

    Um die Standardeinstellungen für künftige Minitab-Sessions zu ändern, wählen Sie Datei > Optionen > Einzelne Befehle > Verteilungen aus.

Dieses Diagramm zeigt beispielsweise eine negative Binomialverteilung, die die Gesamtzahl der Versuche modelliert und eine Ereigniswahrscheinlichkeit von 0,5 sowie 5 Ereignisse aufweist.

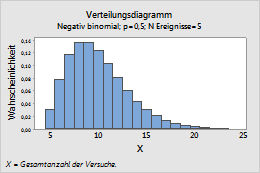
Normal

Führen Sie die folgenden Schritte aus, um die Parameter für die Normalverteilung einzugeben.

  1. Geben Sie im Feld Mittelwert den Wert für das Zentrum der Verteilung ein.
  2. Geben Sie im Feld Standardabweichung den Wert für die Streubreite der Verteilung ein.

Dieses Diagramm stellt z. B. eine Normalverteilung mit dem Mittelwert 0 und der Standardabweichung 1 dar.

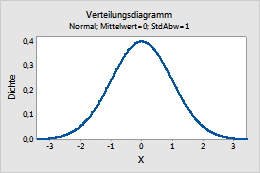
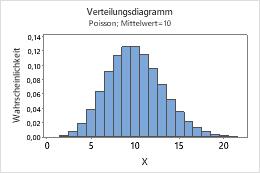
Poisson

Geben Sie im Feld Mittelwert den Wert für die durchschnittliche Ereignisrate ein. Weitere Informationen finden Sie unter Poisson-Verteilung.

Dieses Diagramm stellt beispielsweise eine Poisson-Verteilung mit dem Mittelwert 10 dar.

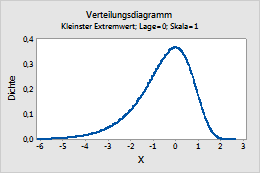
Kleinster Extremwert

Führen Sie die folgenden Schritte aus, um die Parameter für die Verteilung des kleinsten Extremwerts einzugeben. Weitere Informationen finden Sie unter Verteilung des größten und des kleinsten Extremwerts.

  1. Geben Sie im Feld Lage einen Wert ein, der die Lage der Verteilungsspitze darstellt.
  2. Geben Sie im Feld Skala einen Wert ein, der die Streubreite der Verteilung darstellt.

Dieses Diagramm stellt beispielsweise eine Verteilung des kleinsten Extremwerts mit der Lage 0 und der Skala 1 dar.

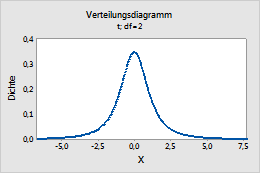
t

Geben Sie im Feld Freiheitsgrade die Freiheitsgrade ein, mit denen die t-Verteilung definiert werden sollen. Weitere Informationen finden Sie unter t-Verteilung.

Dieses Diagramm stellt beispielsweise eine t-Verteilung mit 2 Freiheitsgraden dar.

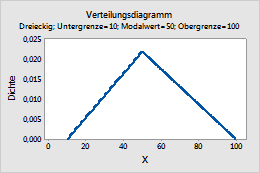
Dreieck

Führen Sie die folgenden Schritte aus, um die Parameter für die Dreiecksverteilung einzugeben.

  1. Geben Sie im Feld Unterer Endpunkt das Minimum für die Verteilung ein.
  2. Geben Sie im Feld Modalwert den Wert für die Spitze der Verteilung ein.
  3. Geben Sie im Feld Oberer Endpunkt das Maximum für die Verteilung ein.

Dieses Diagramm stellt beispielsweise eine Dreiecksverteilung mit dem unteren Endpunkt 10, dem Modalwert 50 und dem oberen Endpunkt 100 dar.

Gleichverteilung

Führen Sie die folgenden Schritte aus, um die Parameter für die Gleichverteilung einzugeben.

  1. Geben Sie im Feld Unterer Endpunkt das Minimum für die Verteilung ein.
  2. Geben Sie im Feld Oberer Endpunkt das Maximum für die Verteilung ein.

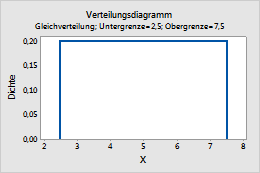
Dieses Diagramm zeigt z. B. eine Gleichverteilung mit dem unteren Endpunkt 2,5 und dem oberen Endpunkt 7,5.

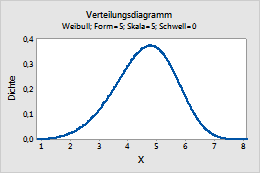
Weibull

Führen Sie die folgenden Schritte aus, um die Parameter für die Weibull-Verteilung einzugeben.

  1. Geben Sie im Feld Formparameter einen Wert ein, der die Form der Verteilung darstellt.
  2. Geben Sie im Feld Skalenparameter einen Wert ein, der die Skala der Verteilung darstellt.
  3. Geben Sie im Feld Schwellenwertparameter die Untergrenze der Verteilung ein.

Dieses Diagramm stellt beispielsweise eine Weibull-Verteilung mit der Lage 5, der Skala 5 und dem Schwellenwert 0 dar.

Copyright © 2024 Minitab, LLC. All rights Reserved.