Welche Grafiken kann ich in der Web-App bearbeiten?
- Streudiagramm
- Matrixplot
- Blasendiagramm
- Randdiagramm
- Histogramm
- Punktdiagramm
- Wahrscheinlichkeitsnetz
- Diagramm der empirischen Verteilungsfunktion
- Darstellung der Wahrscheinlichkeitsverteilung
- Boxplot
- Fehlerbalkendiagramm
- Einzelwertdiagramm
- Liniendiagramm
- Balkendiagramm
- Tortendiagramm
- Zeitreihendiagramm
- Flächendiagramm
- Konturdiagramm
- 3D-Streudiagramm
- 3D-Wirkungsflächendiagramm
Hinweis
Sie können die obigen Grafiken nur bearbeiten, wenn Sie sie über das Menü Grafik erstellt haben. Sie können keine Grafiken bearbeiten, die über Befehle im Menü Statistik generiert wurden.
So bearbeiten Sie eine Grafik
So bearbeiten Sie eine der obigen Grafiken in der Web-App:
- Erstellen Sie Ihre Grafik.
- Klicken Sie im Ausgabebereich mit der rechten Maustaste auf die Grafik, oder klicken Sie auf die Grafik und klicken Sie auf
 , und wählen Sie dann Grafikoptionen aus.
, und wählen Sie dann Grafikoptionen aus. - Die Optionen für die Grafikbearbeitung in der Web-App variieren für jede Grafik. Nehmen Sie die gewünschten Änderungen im rechten Bereich vor. Die Grafik wird automatisch aktualisiert, wenn Sie eine Änderung vornehmen.
Textanmerkungen
Zu den Optionen für Textanmerkungen gehören Titel, Untertitel, Fußnoten und Achsenbeschriftungen. Im Standardtitel für eine Grafik werden der Typ der Grafik sowie die in der Grafik dargestellten Variablen angegeben. Einige Grafiken weisen darüber hinaus standardmäßige Untertitel und Fußnoten auf.
Datendarstellungen
Sie können die für Boxplot, Fehlerbalkendiagramm und Einzelwertdiagramm angezeigten Daten ändern.
- Box für den Interquartilbereich (nur Boxplot)
- Zeigt Boxen für den Interquartilbereich an, die die mittleren 50 % der Daten darstellen. Die Whisker reichen bis zu den maximalen und minimalen Datenpunkten innerhalb von 1,5 Boxenhöhen.
- Ausreißersymbole (nur Boxplot)
- Zeigt Ausreißer auf einem Boxplot an. Ein Ausreißer ist eine ungewöhnlich große oder kleine Beobachtung.
- Symbol für Median
- Zeigt ein Symbol an, das den Mittelpunkt der Daten angibt.
- Box für Konfidenzintervall des Medians
- Zeigt die Box für das Konfidenzintervall des Medians an, in der die 95 %-Konfidenzintervalle für den Median anzeigt werden.
- Box für Spannweite (nur Boxplot)
- Zeigt eine Box an, die vom minimalen Wert bis zum maximalen Wert reicht.
- Verbindungslinie für Median
- Zeigt eine Verbindungslinie an, die die Mediane verbindet, wenn Ihr Grafik mehrere Gruppen enthält.
- Balken für Mittelwert
- Zeigt einen Balken an, der den Mittelwert der Kategorien darstellt.
- Symbol für Mittelwert
- Zeigt ein Symbol an, das den Durchschnitt der Daten angibt.
- Balken für Konfidenzintervall des Mittelwerts
- Zeigt das Feld für das mittlere Konfidenzintervall an, in dem die 95 %-Konfidenzintervalle für den Mittelwert angezeigt werden.
- Verbindungslinie für Mittelwert
- Zeigt eine Verbindungslinie an, die die Mittelwerte verbindet, wenn Ihre Grafik mehrere Gruppen enthält.
- Symbole für Einzelwerte
- Stellt jeden Datenpunkt in der Grafik dar.
Skalen
Skalen für Streudiagramme
- Logarithmus
- Eine logarithmische Skala linearisiert logarithmische Beziehungen durch Ändern der Achse, sodass der gleiche Abstand unterschiedlich große Änderungen der Werte entlang der Skala darstellt. In einem Streudiagramm mit einer nicht transformierten x-Skala ist die Funktion y = ln(x) beispielsweise nicht linear. Wenn Sie die x-Skala mit dem natürlichen Logarithmus (Basis e) transformieren, ist die Form der Daten linear.
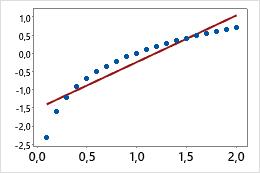
Nicht transformierte x-Skala
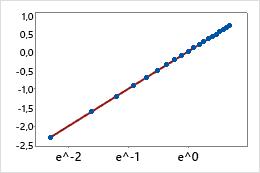
Transformierte x-Skala (Transformation mit Logarithmus zur Basis e)
Hinweis
Sie können keine logarithmische Skala verwenden, wenn die Daten auch nicht positive Werte enthalten.
- Potenz
- Für eine Potenztransformation werden die Datenwerte mit dem angegebenen Wert potenziert, und die Skala bleibt linear. Im Streudiagramm mit der nicht transformierten x-Skala folgt die Krümmung der Daten beispielsweise nicht der linearen angepassten Regressionslinie. Wenn Sie eine Potenztransformation der x-Skala durchführen, folgen die Daten der linearen angepassten Regressionslinie.
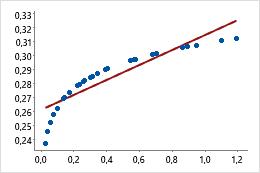
Nicht transformierte x-Skala
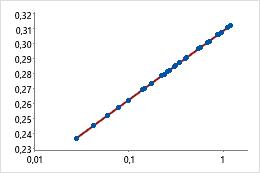
Transformierte x-Skala (Potenztransformation)
Skalen für Histogramme
Einteilungen sind Intervalle mit gleichen Abständen zum Sortieren von Stichprobendaten für die Darstellung in Grafiken. In Minitab wird in Histogrammen die Anzahl der Werte innerhalb der einzelnen Einteilungen dargestellt.
Einteilungen können über ihren Mittelpunkt (Zentralwert) oder ihre Trennwerte (Grenzen) definiert werden. Die Darstellung der Grafik ändert sich, wenn Sie die Intervalle mit einer anderen Methode definieren.
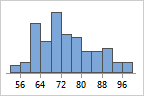
- Mittelpunkt
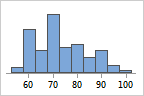
- Trennwert
Die Anzahl von Einteilungen wirkt sich auf die Darstellung einer Grafik aus. Bei zu wenigen Einteilungen ist die Grafik zu grob und stellt die Daten nicht angemessen dar. Bei zu vielen Einteilungen enthalten viele von diesen keine Werte, und die Grafik weist möglicherweise zu viele Details auf.
Beispielsweise werden in den folgenden Histogrammen die gleichen Daten mit einer unterschiedlichen Anzahl von Einteilungen veranschaulicht. Minitab berechnet und verwendet automatisch die optimale Anzahl von Einteilungen. Die mittlere Grafik (15 Einteilungen) bildet den Standard von Minitab für diese Daten.
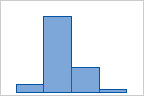
4 Einteilungen
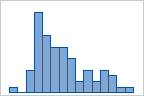
15 Einteilungen
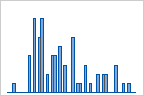
50 Einteilungen
Y-Skalentyp für Histogramm
- Häufigkeit
- Die Höhe jedes Balkens stellt die Anzahl der Beobachtungen in der Einteilung dar.
- Prozent
- Die Höhe jedes Balkens stellt den Prozentsatz der Stichprobenbeobachtungen in der Einteilung dar. Ein Histogramm mit einer Skala von Prozentsätzen wird gelegentlich auch als Histogramm der relativen Häufigkeiten bezeichnet. Verwenden Sie eine Skala von Prozentsätzen, um Stichproben mit unterschiedlichen Stichprobenumfängen zu vergleichen.
- Dichte
- Die Fläche jedes Balkens stellt den Anteil der Stichprobenbeobachtungen in der Einteilung dar (Anteil = Fläche des Balkens = Breite der Einteilung × Höhe des Balkens).
- Werte einteilungsübergreifend kumulieren
- (Nur Häufigkeits- und Prozentskalen) Die Höhen der Balken werden von links nach rechts kumuliert. Die Höhe jedes Balkens entspricht der Höhe der Einteilung plus aller vorhergehenden Einteilungen
Y-Skala für Wahrscheinlichkeitsnetz
- Prozent
- Die Werte auf der y-Achse stellen die geschätzten kumulativen Prozentsätze dar. Der geschätzte kumulative Prozentsatz ist gleich dem Produkt aus der geschätzten kumulativen Wahrscheinlichkeit und 100.
- Wahrscheinlichkeit
-
Die Werte auf der y-Achse stellen die geschätzten kumulativen Wahrscheinlichkeiten dar. Die kumulative Wahrscheinlichkeit für einen Wert x ist die Wahrscheinlichkeit, dass eine zufällige aus der Grundgesamtheit gewählte Beobachtung kleiner oder gleich x ist.
Minitab verwendet die Median-Rang-Methode (die auch als Benard-Methode bezeichnet wird), um die kumulative Wahrscheinlichkeit (r) für jede Beobachtung zu schätzen:
r = (i – 0,3) / (n + 0,4)
In dieser Formel ist i der Rang der Beobachtung in der Stichprobe, und n ist die Gesamtzahl der Beobachtungen in der Stichprobe. Für den kleinsten Wert in der Stichprobe ist i = 1, für den größten Wert in der Stichprobe i = n.
- Wert
-
Die Werte auf der y-Achse stellen die inversen kumulativen Wahrscheinlichkeiten dar.
Die Werte für die Normalverteilung und die lognormale Verteilung sind die inverse kumulative Wahrscheinlichkeit von r, die anhand der Standardnormalverteilung berechnet wird.
Die Werte für die Exponentialverteilung und die Weibull-Verteilung werden mit LN(–LN(1–r)) berechnet, wobei LN der natürliche Logarithmus ist.
Y-Skala für Balkendiagramm
Sie können die y-Skala in einem Balkendiagramm in eine Prozentskala, eine kumulative Skala oder beides ändern.
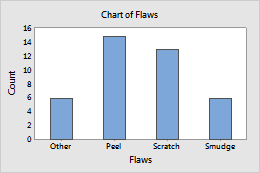
Standard-y-Skala
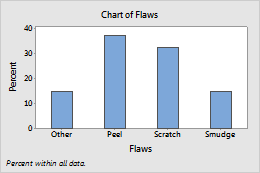
Y als Prozentsatz anzeigen ausgewählt
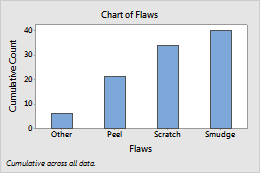
Y über X kumulieren ausgewählt
Sie können angeben, ob die Berechnungen von Prozentsätzen und die Kumulierung von Werten über das gesamte Diagramm oder innerhalb der Kategorien der angegebenen Variablen erfolgen sollen.
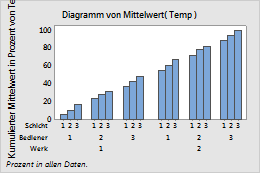
- Über alle Kategorien
- Wenn Sie Über alle Kategorien auswählen, werden die Balken über das gesamte Diagramm auf 100 % kumuliert.
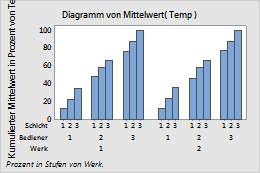
- Innerhalb von Kategorien der Stufe 1 (äußerste)
- Wenn Sie Innerhalb von Kategorien der Stufe 1 (äußerste) auswählen, werden die Balken innerhalb jeder einzelnen Stufe von „Werk“ auf 100 % kumuliert.
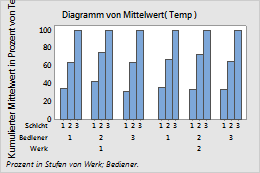
- Innerhalb von Kategorien der Stufe 2
- Wenn Sie Innerhalb von Kategorien der Stufe 2 auswählen, werden die Balken innerhalb jeder einzelnen Stufe von „Bediener“ auf 100 % kumuliert.
Reihenfolge
Sie können die Reihenfolge der Balken in Balkendiagrammen und die der Segmente in Tortendiagrammen ändern.
- Standard
- Für die Anzahl von eindeutigen Werten stellt Minitab die eindeutigen Werte in aufsteigender Reihenfolge dar.
- Ansteigenden Y-Werten
- Ordnet die Balken oder Segmente vom kleinsten zum größten.
- Abfallenden Y-Werten
- Ordnet die Balken oder Segmente vom größten zum kleinsten.
Anpassungen
Eine angepasste Regressionslinie in einer Grafik stellt die mathematische Regressionsgleichung für Ihre Daten dar. Verwenden Sie eine angepasste Verteilungslinie, um zu untersuchen, wie gut die Stichprobendaten einer bestimmten theoretischen Verteilung folgen.
Sie können die Verteilungsanpassung für Streudiagramme, Histogramme und Diagramme der Wahrscheinlichkeitsverteilung in der Minitab-Web-App hinzufügen oder bearbeiten. Weitere Informationen zu den verfügbaren Verteilungen finden Sie unter Verteilungen für Anpassungslinien.
Linien
Referenzlinien sind horizontale oder vertikale Linien, die sich über den Datenbereich einer Grafik erstrecken und Ziele oder Grenzen kennzeichnen.
Mit Gitterlinien wird ein Raster im Hintergrund angelegt, dessen Linien an den Positionen der Haupt- und Unterteilstriche verlaufen und als Referenzpunkte in Ihrer Grafik dienen.
Beschriftungen
Datenbeschriftungen geben Ihnen Informationen über einzelne Elemente der dargestellten Daten in einer Grafik. Die Daten werden je nach Grafik unterschiedlich dargestellt. Datenbeschriftungen basieren auf Variablen und Daten, die in der Grafik verwendet werden.
Hinweis
In der Minitab-Desktop-App können Sie Spalten mit benutzerdefinierten Beschriftungen angeben.
Ausrichtung
Für viele Grafiken können Sie entweder eine vertikale oder horizontale Anzeigeausrichtung angeben.
