请选择您所选的方法或公式。
公差区间的样本数量的一般公式
公差区间(双侧)的定义
假设 X1, X2, ..., Xn 是来自某个连续分布中数量为 n 的随机样本的排序值。假设维度大于或等于 1 的某个参数空间中 Ω 的分布函数为 F(χ,θ)。
假设 L < U 是两个基于样本的统计量,对于任何给定值 α 和 P(0 < α < 1,0 < P < 1),以下等式针对 Ω 中的每个 θ 都成立:
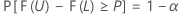
然后,区间 [L, U] 是双侧公差区间,其容量 = P x 100%,置信区间 = 100(1 - α)%。类似的区间可称为双侧 (1 - α, P) 公差区间。例如,如果 α = 0.10,P = 0.85,则生成的区间称为双侧 (90%, 0.85) 公差区间。
样本数量和边际误差
假设 C = F(U) – F(L)。双侧 (1 –α, P) 公差区间如下所示: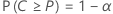
- 区间将至少涵盖 100P% 总体的概率为 1 – α。
- 概率 α* 很小,区间将涵盖多于 100P* % 的总体,其中 P* = P + ε,ε > 0。
换句话说,对于 P、α、ε 和 α* 的任何给定值,样本数量是确定的,以便:
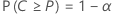
并且

此方法基于如下事实:对于任何 P* > P,P(C>P*) 是样本数量的递减函数,因此可用来评估精确度。
如果选择较小的 ε 和 α*,则会产生使公差区间缩小的效应,因此,需要使用较大的样本数量。ε 和 α* 的典型值为 0.10、0.05 或 0.01。
注意
上面的定义和概念同样适用于单侧公差区间。
- Faulkenberry, G.D. 和 Weeks, D.L. (1968)。《Sample size determination for tolerance limits》(为公差限值确定样本数量)。Technometrics(技术计量学)第 10 期,第 343-348 页。
为正态公差区间计算样本数量
单侧区间
Faulkenberry 和 Daly1 中显示,如果指定了 α、P、ε 和 α* 值,则单侧区间所需的样本数量可以通过查找满足以下方程的最小值 n 来算出:

其中,表示法 tx,y(d) 表示自由度为 x 且非中心参数为 d 的非中心 t 分布的第 y 个百分位数。非中心参数 δ 和 δ* 的计算方式如下:

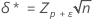
其中,zp 是标准正态分布的第 P 个百分位数。
Minitab 采用迭代算法查找所需的最小值 n。
双侧区间
有关依赖于函数 I( k, n, P) 的双侧区间样本数量的计算,请转到公差区间的方法和公式(正态分布),然后单击“正态分布的精确公差区间”。
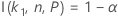
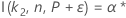
Minitab 采用迭代算法查找所需的最小值 n。有关更多信息,请参见 Odeh、Chou 和 Owen2。
表示法
| 项 | 说明 |
|---|---|
| 1 – α | 公差区间的置信水平 |
| P | 公差区间的范围(区间中的目标最小总体百分比) |
| ε | 公差区间的边际误差 |
| α* | 公差区间的边际误差概率 |
| n | 样本中的观测值个数 |
- Faulkenberry, G.D. 和 Daly, J.C. (1970)。Sample size for tolerance limits on a normal distribution(正态分布公差限的样本数量)。Technometrics(技术计量学),第 12 期,813–21。
- Odeh, R. E. 、Chou, Y.-M. 和 Owen, D. (1987)。The precision for coverages and sample size requirements for normal tolerance intervals(正态公差区间的覆盖范围和样本数量要求的精确度)。Communications in Statistics: Simulation and Computation(统计通讯:模拟与计算),第 16 期,第 969 到 985 页。
为正态公差区间计算区间中最大总体百分比
P* = P + ε
边际误差的计算与公差区间的样本数量的一般公式中所述的样本数量计算相似。
单侧区间
如果指定了 n、α、P 和 α* 值,则单侧区间的边际误差 ε 可以先通过对以下方程中的 δ* 进行求解而算出:
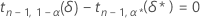
其中,表示法 tx,y(d) 表示自由度为 x 且非中心参数为 d 的非中心 t 分布的第 y 个百分位数。Minitab 使用数值根查找程序例程来计算 δ*。确定了 δ* 值后,可以通过以下公式算出 ε 值:

双侧区间
双侧区间的边际误差的计算依赖于函数 I( k, n, P),如正态分布的精确公差区间中所述。
如果指定了 n、α、P 和 α* 值,将使用 Odeh、Chou 和 Owen1 中所述的算法得出双侧区间的边际误差 ε。首先,对以下方程中的 k 进行求解:
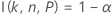

表示法
| 项 | 说明 |
|---|---|
| 1 – α | 公差区间的置信水平 |
| P | 公差区间的范围(区间中的目标最小总体百分比) |
| P* | 区间中最大总体百分比 |
| ε | 公差区间的边际误差 |
| α* | 公差区间的边际误差概率 |
| n | 样本中的观测值个数 |
- Odeh, R. E. 、Chou, Y.-M. 和 Owen, D. (1987)。The precision for coverages and sample size requirements for normal tolerance intervals(正态公差区间的覆盖范围和样本数量要求的精确度)。Communications in Statistics: Simulation and Computation(统计通讯:模拟与计算),第 16 期,第 969 到 985 页。
为非参数公差区间计算样本数量和区间中最大可接受总体百分比
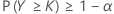
也就是说 n – k = FW–1 (1 – α),其中 FW–1(.) 表示 W = n – Y 的反向累积分布函数。
同样,可以看出单侧 (1 – α, P) 公差上限用 X(n – k + 1) 给定,其中 k 满足上面针对下限的条件。
在这两种情况下,实际范围或有效范围用 P(Y > k) 给定。
另外,双侧 (1 – α, P) 公差区间可以用 (Xr, Xs) 给定,其中 k = s – r 是满足以下条件的最小整数:
常见的做法是取 s = n – r + 1,以便 r = (n – k + 1) / 2。r 和 s 都向下取整到最接近的整数。实际范围或有效范围用 P(V ≤ k – 1) 给定。
标准
非参数公差区间(单侧和双侧)的样本数量计算标准与针对正态数据描述的标准相似。更具体地说,对于单侧 (1 – α, P) 公差下限,计算标准由确定满足以下条件的样本数量 n 和最大整数 k 组成:
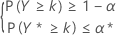
此条件与查找满足以下条件的 n 和最大整数 k 等价:
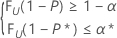
其中 FU(.) 表示随机变量 U 的累积分布函数,该变量采用 α = k 和 b = n – k + 1 参数的 beta 分布形式。
正如在 Hahn 和 Meeker1 中指出的那样,该标准会生成对于单侧公差区间和双侧公差区间相同的样本数量要求。因此,我们对于单侧区间和双侧区间均使用上面的标准。
对于 ε、P 和 α* 的给定值,Minitab 使用迭代算法来查找可满足上述两个条件的最小样本数量。对于 n、p 和 α* 的给定值,Minitab 还将使用迭代算法计算满足以上条件的边际误差,然后使用以下公式计算区间中最大总体百分比的区间。
P* = P + ε
有关其他详细信息,请参见 Hahn 和 Meeker1。
表示法
| 项 | 说明 |
|---|---|
| 1 - α | 公差区间的置信水平 |
| P | 公差区间的范围(区间中的目标最小总体百分比) |
| P* | 区间中最大总体百分比 |
| ε | 公差区间的边际误差 |
| α* | 公差区间的边际误差概率 |
| n | 样本中的观测值个数 |
- Hahn, G. J. 和 Meeker,W. Q.(1991 年),统计区间:从业人员指南 (Statistical Intervals: A Guide for Practitioners)。John Wiley & Sons,第 170 页。
