参数
参数将显示您在对话框中选择的统计量。参数是整个总体的描述性度量,它可用作概率分布函数 (PDF) 的输入以生成分布曲线。有关更多信息,请转到什么是参数、参数估计值和抽样分布?
观测值长度
Poisson 过程对位于特定观测值范围的某个事件或属性的发生次数进行计数,该事件或属性可以表示时间、面积、体积和项数等内容。观测值长度表示每个观测值范围的数量级、持续时间或大小。
解释
Minitab 使用观测值长度将发生率转换为最适合您的情形的形式。
例如,如果每个样本观测值对每年的事件数进行计数,则长度为 1 表示每年的发生率,而长度为 12 则表示每月的发生率。
- 总发生次数为 122,因为检查员发现了 122 个缺陷。
- 样本数量 (N) 为 50,因为检查员抽取 50 箱作为样本。
- 为了确定每条毛巾的缺陷数,检查员使用观测值长度 10,因为每箱有 10 条毛巾。为了确定每箱毛巾的缺陷数,检查员使用观测值长度 1。
- 发生率为(总发生次数/N)/(观测值长度)= (122/50) / 10 = 0.244。因此每条毛巾平均有 0.244 个缺陷。
分布
- 正态
-
正态分布是钟形分布,在其中,距离均值的连续标准差建立了用于估计数据观测值的百分比的基准。这些基准是 Z 检验和 t 检验等许多假设检验的基础。
例如,居住在宾夕法尼亚州的所有成年男性的身高近似于正态分布。因此,大多数男性的身高都将接近于 69 英寸的平均身高。类似数量的男性的身高都比 69 英寸稍高或稍矮。只有一小部分人身材特别高或特别矮。
- 二项
-
当您将项、事件或人员单独分到一个类别(共两个类别)中时,一个类别中的项、事件或人员数量服从二项分布。两个类别应当互斥,如是/否、通过/未通过或缺陷/非缺陷。
例如,工程师检查一批螺栓样本以找出导致其不能使用的严重裂纹。没有裂纹的螺栓没有缺陷,有裂纹的螺栓则有缺陷。
- Poisson
-
当您对某个时间段、地区或其他观测值长度内的特征、结果或活动进行计数时,您将得到 Poisson 数据。Poisson 数据按大小相同的每个单元的计数进行评估。
例如,公共汽车公司的检查员对 30 天内汽车每天出现的故障进行计数。
标准差
标准差是离差的最常用度量,即数据从均值展开的程度。符号 σ(西格玛)通常用于表示总体的标准差,而 s 用于表示样本的标准差。对某一过程而言随机或合乎自然规律的变异通常称为噪声。Minitab 显示您在对话框中指定的计划值。
比率
比率是整体的相对部分,与计数或频率相反。比率等于事件数除以样本数量。Minitab 显示您在对话框中指定的计划值。
率
发生率是在观测值的每个单位长度内,发生事件的平均次数。Minitab 显示您在对话框中指定的计划值。
均值
Poisson 均值是在总观测值空间内事件出现的平均次数。Minitab 显示您在对话框中指定的计划值。
置信水平
通常,置信水平为 95% 即可。这表明来自同一总体的 20 个样本中有 19 个 (95%) 会生成包含总体参数的置信区间。
置信水平表示在反复从同一个总体中抽取样本时,将包括总体参数的区间所占的百分比。因此,如果您收集 100 个样本,而且创建了 100 个 95% 置信区间,则应当得到约 95 个包含总体参数(如总体的均值)的区间,如下图中所示。
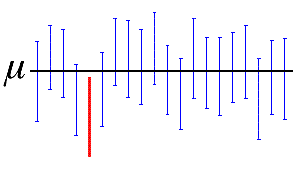
在该图中,水平线表示未知总体均值 µ 的固定值。与水平线相交的 19 个垂直的蓝色置信区间中包含总体均值。完全位于水平线下方的 1 个红色置信区间不包含总体均值。
置信区间
Minitab 显示您在对话框中指定的置信区间的类型。
置信区间提供总体比率的可能值范围。由于样本的随机性,来自总体的两个样本不可能生成相同的置信区间。但是如果将样本重复许多次,则所获得的特定百分比的置信区间或限值会包含未知的总体参数。这些包含参数的置信区间或限值的百分比是区间的置信水平。
上限定义可能大于总体参数的值。下限定义可能小于总体参数的值。
