可通过完成以下步骤来解释单样本等价检验。主要输出包括差值的估计值、置信区间、等价图和其他图形。
第 1 步:确定总体均值与目标是否等价
将置信区间与等价限值进行比较。如果置信区间完全在等价限值范围内,则可以声明总体均值等于目标值。如果部分置信区间超出等价限值,则无法声明等价。
差值: 均值(力度) - 目标值
| 差值 | SE | 对等项的 95% CI | 等价区间 |
|---|---|---|---|
| 0.28500 | 0.13831 | (0, 0.520586) | (-0.42, 0.42) |
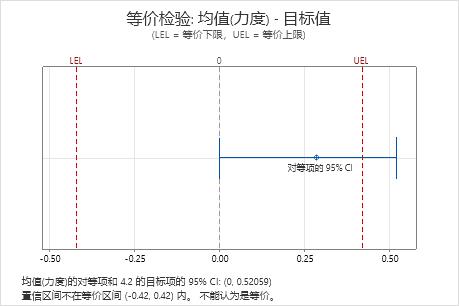
主要结果:95% 置信区间,等价区间
在这些结果中,95% 置信区间超出了等价上限。因此,您无法声明总体均值等于目标值。
注意
如果您选择使用备择假设来检验不等价性(而非等价性),请通过将置信区间的下限与等价下限进行比较,或者将置信区间的上限与等价上限进行比较,评估整体结果。有关更多信息,请转到单样本等价检验 的差值并单击“下限”或“上限”。
步骤 2:检查数据是否有问题
您数据中存在的问题(如偏度或异常值)可对结果产生不利影响。可使用图形来查找偏度(通过检查数据的散布)以及确定可能的异常值。
确定数据是否偏斜
如果数据偏斜,则大多数数据会靠近于图形的高端或低端。通常情况下,在箱线图或直方图中最易于标识偏度。
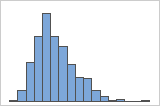
右偏斜
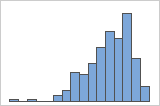
左偏斜
例如,右偏斜的直方图显示薪金数据。很多员工的薪金相对较低,而薪金较高的员工越来越少。左偏斜的直方图显示故障率数据。少数项目在早些时候发生故障,而在后期发生故障的项目逐渐增多。
如果您的样本较小(小于 20 个值),严重偏斜的数据可能会影响检验结果的有效性。如果您的数据严重偏斜,并且样本较小,请考虑增大样本数量。
识别异常值
异常值是远离其他数据的数据点,可能会显著影响您的结果。在箱线图上最容易识别异常值。
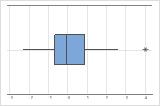
在箱线图上,异常值用星号 (*) 标识。
您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。可以考虑删除与特殊原因相关的数据,然后重新执行分析。有关特殊原因的更多信息,请转到使用控制图检测常见原因变异和特殊原因变异。
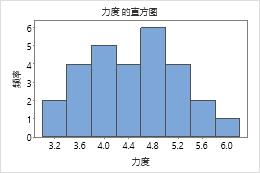
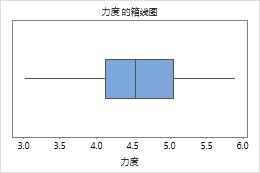
在这些图形中,数据看上去不偏斜,而且没有异常值。
