多重比较检验
k > 2 样本的多重比较区间
设 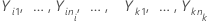 为 k > 2 个独立样本,每个样本都是独立的,分布方式也相同,并且均值为
为 k > 2 个独立样本,每个样本都是独立的,分布方式也相同,并且均值为 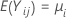 且方差
且方差  。并且,假设样本源自具有共同峰度的总体。
。并且,假设样本源自具有共同峰度的总体。 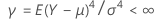
设 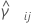 作为样本对 ( i, j) 的合并峰度估计值,表达式如下:
作为样本对 ( i, j) 的合并峰度估计值,表达式如下:
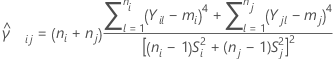
设 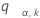 是一系列独立和相同分布的标准正态随机分布的 k 变量的上限点。即,
是一系列独立和相同分布的标准正态随机分布的 k 变量的上限点。即,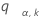 满足以下条件:
满足以下条件:
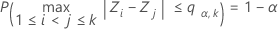
其中 Z1, ..., Zk 是独立和相同分布的标准正态随机变量。Barnard (1978) 基于用于计算正常范围的分布函数的 16 点 Gaussian 求积提供了一种简单的数值算法。
当且仅当至少一对下列区间不重叠时,多重比较过程会否定等方差(也称为同质方差)的原假设:
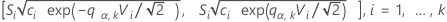
其中
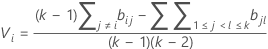
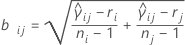
其中 ri = (ni - 3) / ni.
我们将上述区间称为多重比较区间或 MC 区间。每个样本的 MC 区间不会解释为父总体的标准差的置信区间。Hochberg 等人 (1982) 将将比较均值的类似区间称为“不确定区间”。这里指定的 MC 区间仅对比较多样本设计的标准差或方差有效。当总体多重比较检验显著时,与非重叠区间相对应的标准差在统一意义上不同。(有关这些区间的详细意义,请参阅多重比较方法上的白皮书)。
k = 2 个样本的多重比较区间
在只有两个样本的情况下,多重比较区间的公式如下:

其中,zα / 2 是标准正态分布的 α / 2 百分位点上限,ci = ni / ni - zα / 2,且 Vi 由以下公式得出:
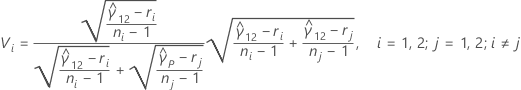
检验的 p 值
如果设计中有 2 个样本,则 Minitab 会使用双方差检验和假设比率 Ρo 为 1 的 Bonett 方法计算多重比较检验的 p 值。
如果设计中有 k > 2 个样本,则设 Pi j 为任意对 (i, j ) 样本的检验 p 值。多重比较过程的 p 值作为等方差的整体检验,公式如下:

有关更多信息,包括计算 Pi j 的模拟和详细算法,请转到 Bonett 方法(这是一本白皮书,其中包含有关 Bonett 方法的模拟和其他信息)。
表示法
| 项 | 说明 |
|---|---|
| ni | 样本 i 中的观测值个数 |
| Y i l | 样本 i 中的第 l 个观测值 |
| mi | 具有以下修剪比率的样本 i 的调整比率: |
| k | 样本数 |
| Si | 样本 i 的标准差 |
| α | 检验的显著性水平 = 1 - (置信水平 / 100) |
| Ci | 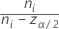 |
| Zα / 2 | 标准正态分布的 α / 2 百分位点上限 |
| ri |  |
Levene 检验统计量
Minitab 显示 Levene 检验的检验统计量和 p 值。原假设是方差相等,备择假设为方差不相等。当数据来自连续但不一定正态的分布时,请使用 Levene 检验。
Levene 检验的计算方法是 Levene 程序 (Levene, 1960) 的修正,该程序由 Brown 和 Forsythe (1974) 联合开发。此方法考虑的是观测值与样本中位数之间的距离,而不是与样本均值之间的距离。采用样本中位数而不是样本均值,从而使该检验对于较小样本更有效,并且使程序实现渐近自由分布。如果 p 值小于 α 水平,则否定方差相等的原假设。
公式
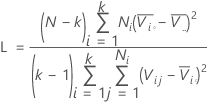
- H. Levene (1960),Contributions to Probability and Statistics(对概率和统计量的贡献),Stanford University Press, CA.
- M. B. Brown 和 A. B. Forsythe (1974),“Robust tests for the equality of variance”(针对方差相等性的强大检验),Journal of the American Statistical Association(美国统计协会杂志),第 69 期,第 364 到 367 页。
表示法
| 项 | 说明 |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
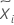 | 中位数 |
Bartlett 检验的统计量
Minitab 显示 Bartlett 检验的检验统计量和 p 值。当只有两个水平时,Minitab 将执行 F 检验而非 Bartlett 检验。对于这些检验,原假设是方差相等,备择假设为方差不相等。当数据呈正态分布时,使用 Bartlett 检验;Bartlett 检验不适合偏离正态分布的情况。
Bartlett 检验统计量根据自由度,计算每个样本方差的加权算术平均值和加权几何平均值。平均值的差值越大,样本方差不相等的可能性越大。B 服从 χ2 分布,自由度为 k – 1。如果 p 值小于 α 水平,则否定方差相等的原假设。
公式
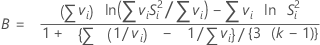
表示法
| 项 | 说明 |
|---|---|
| si2 |  |
| k | 样本数 |
| vi | ni - 1 |
| ni | 处于第 i 个因子水平的观测值数 |
F 检验统计量
当只有两个水平时,Minitab 将执行 F 检验而非 Bartlett 检验。原假设是方差相等,备择假设为方差不相等。当数据来自正态分布时,请使用 F 统计量。
如果 p 值小于 α 水平,则否定方差相等的原假设。
公式
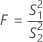
p 值的公式
- 对于具有“小于”备择假设的单侧检验,p 值等于从自由度为 DF1 和 DF2 的 F 分布中获得等于或小于观测值的 F 统计量的概率。
- 对于比值小于 1 的双侧检验,p 值等于 F 曲线下方面积的两倍,小于自由度为 DF1 和 DF2 的 F 分布中的观测值。
- 对于比值大于 1 的双侧检验,p 值等于 F 曲线下方面积的两倍,大于自由度为 DF1 和 DF2 的 F 分布中的观测值。
- 对于具有“大于”备择假设的单侧检验,p 值等于从自由度为 DF1 和 DF2 的 F 分布中获得等于或大于观测值的 F 统计量的概率。
表示法
| 项 | 说明 |
|---|---|
| S12 | 样本 1 的方差 |
| S22 | 样本 2 的方差 |
| n1 - 1 | 分子自由度 |
| n2 - 1 | 分母自由度 |
标准差 (StDev)
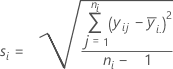
表示法
| 项 | 说明 |
|---|---|
| yij | 处于第 i 个因子水平的观测值 |
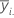 | 处于第 i 个因子水平的观测均值 |
| ni | 处于第 i 个因子水平的观测值数 |
Bonferroni 置信区间
Minitab 使用 Bonferroni 方法来计算标准差的置信区间。置信区间是可能包含部分总体参数的值范围,在此情况下,其包含标准差。
标准置信区间采用置信水平 1 – α / 2 来计算。Bonferroni 方法针对各个置信区间采用置信水平 1 – α / 2p,其中,p 是因子和水平组合数。此方法可确保置信区间集具有至少为 1 – α 的置信水平。Bonferroni 方法提供更多的保守(较宽)置信区间,这会减少类型 1 误差的概率。
