关于本主题
公差区间方法
- 对数正态
- Gamma
- 指数
- 最小极值
- Weibull
- 最大极值
- Logistic
- 对数 Logistic
一般定义
设 X 1, X 2, ..., X n 为基于部分连续分布中数量为 n 的随机样本的排序统计量。
假设维度大于或等于 1 的某个参数空间中 Ω 的分布函数为 F(χ;θ)。
假设 L < U 是两个基于样本的统计量,对于任何给定值 α 和 P(0 < α < 1,0 < P < 1),以下等式针对 Ω 中的每个 θ 都成立:
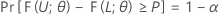
然后,区间 [L, U] 是双侧公差区间,其容量 = P x 100%,置信区间 = 100(1 – α)%。类似的区间可称为双侧 (1 – α, P) 公差区间。例如,如果 α = 0.10,P = 0.85,则生成的区间称为双侧 (90%, 0.85) 公差区间。
如果 L = –∞ 且 U < +∞,则区间 (-∞, U] 称为单侧 (1 – α, P) 公差上限。如果 L > -∞ 且 U = +∞,则区间 [L, +∞) 称为单侧 (1 – α, P) 公差下限。
- 单侧 (1 – α, P) 公差下限也是单侧 (P, 1 – α) 公差上限。
- 数据分布的第 (1 – P) 个百分位数的单侧 (1 – α)100% 置信下限也称为单侧 (1 – α, P) 公差下限。同样地,数据分布的第 P 个百分位数的单侧 (1 – α)100% 置信上限也称为单侧 (1 – α, P) 公差上限。
- 如果 L 和 U 是单侧 (1 – α/2, (1 + P)/2) 公差上限和下限,则 [L, U] 是近似双侧 (1 – α, P) 公差区间。此方法可以在无法直接获得双侧公差区间的情况下使用。生成的双侧公差区间通常是保守的区间。请参见 Guenther1 以及 Hahn 和 Meeker2。
- Guenther, W. C. (1972)。Tolerance intervals for univariate distributions(单变量分布的公差区间),Naval Research Logistics(海军物流研究),第 19 期:第 309 到 333 页。
- Hahn G. J. 和 Meeker W. Q. (1991)。Statistical Intervals: A Guide for Practitioners(统计间隔:从业者指南)。纽约 John Wiley & Sons。
连续分布的精确非参数公差区间
Minitab 计算精确的 (1 – α, P) 非参数公差区间,其中 1 – α 是置信水平,P 是范围(区间中的目标最小总体百分比)。公差区间的非参数方法是与分布无关的方法。换言之,非参数公差区间不取决于样本的父总体。Minitab 将对单侧和双侧区间使用精确方法。
设 X 1, X 2 , ... , X n 为基于部分连续分布总体 F(x;θ) 中随机样本的排序统计量。那么,根据 Wilks1, 2 和 Robbins3 的发现,可以得出:

其中 B 表示具有参数 a = r 和 b = n – s + 1 的 Beta 分布的累积分布函数。因此,(Xr, Xs) 是与分布无关的公差区间,因为区间范围具有使用已知参数值的 Beta 分布,这些值独立于父总体 F(x;θ) 的分布。
单侧区间
设 k 为满足如下条件的最大整数:

其中 Y 是使用 n 和 1 – P 参数的二项式随机变量。可以看出(请参见 Krishnamoorthy 和 Mathew4),单侧 (1 – α, P) 公差下限由 Xk 给定。相同地,单侧 (1 – α, P) 公差上限由 X n - k +1 给定。在这两种情况下,实际范围或有效范围由 P(Y > k) 给定。
双侧区间
设 k 为满足如下条件的最小整数:

其中 V 是使用 n 和 P 参数的二项式随机变量。因此,
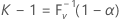
其中,F V -1(x) 是 V 的逆累积分布函数。可以看出(请参见 Krishnamoorthy 和 Mathew4),双侧 (1 – α, P) 公差区间可以由 (Xr, Xs) 给定。Minitab 选择 s = n - r + 1,以便 r = (n – k + 1) / 2。r 和 s 向下舍入到最近的整数。实际范围或有效范围由 P(V < k – 1) 给定。
表示法
| 项 | 说明 |
|---|---|
| 1 – α | 公差区间的置信水平 |
| P | 公差区间的范围(区间中的目标最小总体百分比) |
| n | 样本中的观测值个数 |
- Wilks, S. S. (1941)。Sample size for tolerance limits on a normal distribution(正态分布公差限的样本数量)。The Annals of Mathematical Statistics(数理统计年报),第 12 期,第 91 到 96 页。
- Wilks, S. S. (1941)。Statistical prediction with special reference to the problem of tolerance limits(特别针对公差限问题的统计预测)。The Annals of Mathematical Statistics(数理统计年报),第 13 期,第 400 到 409 页。
- Robbins, H. (1944)。On distribution-free tolerance limits in random sampling(关于随机抽样中与分布无关的公差限)。The Annals of Mathematical Statistics(数理统计年报),第 15 期,第 214 到 216 页。
- Krishnamoorthy, K. 和 Mathew, T. (2009)。Statistical Tolerance Regions: Theory, Applications, and Computation(统计公差领域:理论、应用和计算)。Wiley, Hoboken, NJ.
对数正态分布
- Minitab 取数据的自然对数。
- Minitab 使用正态分布的公差区间过程来计算已变换数据的公差区间。
- Minitab 对从上一步中获得的公差区间限值取指数,以将区间变换为原始数据的尺度。
Gamma 分布的近似公差区间
Gamma 分布的公差区间使用正态分布的近似法。Krishnamoorthy 等人开展的模拟研究显示,该近似法可以提供准确的结果。这些计算遵循以下过程:
- Minitab 取数据的立方根。
- Minitab 使用正态分布的公差区间过程来计算已变换数据的公差区间。
- Minitab 对从上一步中获得的公差区间限值取指数,以将区间变换为原始数据的尺度。
- Krishnamoorthy K.、Mathew T 和 Mukherjee S (2008)。Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability(Gamma 分布基于正态的方法:预测和公差区间及压力强度可靠性)。Technometrics(技术计量学),第 50 期,第 69 到 78 页。
指数分布
Minitab 计算精确的 (1 – α, P) 公差区间,其中 1 – α 是置信水平,P 是范围(区间内人口的目标最小比例)。单侧公差限和双侧公差区间的计算公式有所不同。
单侧指数公差限
此公式将给定下限:
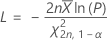
此公式将给定上限:

双侧指数置信区间
Minitab 使用 Newton 方法对以下方程系统进行求解。有关更多详细信息,请参见 Fernandez1。
此公式将给定双侧区间:

其中,

并且 k 1 值取决于此方程系统的解:

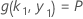
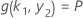
其中
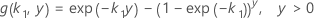
表示法
| 项 | 说明 |
|---|---|
| n | 样本大小 |
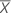 | 样本均值 |
| P | 区间内人口的目标最小比例 |
 | 自由度为 2n 的卡方分布的第 α 个百分位数 |
| α | 1 − 置信水平 |
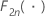 | 自由度为 2n 的卡方分布的累积分布函数 |
- Fernandez, Arturo J. (2010)。Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations(指数情况中的双侧公差区间:勘误和归纳)。Computational Statistics and Data Analysis(计算统计与数据分析),第 54 期,第 151 到 162 页。
最小极值分布
Minitab 根据 Lawless1 计算精确的 (1 – α, P) 公差区间,其中 1 – α 是置信水平,P 是范围(区间中的目标最小总体百分比)。
精确的单侧最小极值公差限
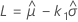
其中


其中
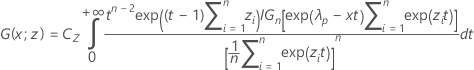
其中

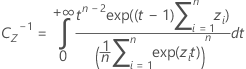
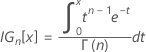
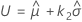
将用于计算 k 1 的公式中的 α 替换为 1 − α,并将 P 替换为 1 − P 后可获得值 k 2。
近似双侧最小极值公差区间
要计算近似双侧区间,请在用于计算单侧公差限的公式中,将 α 替换为 α/2,并将 P 替换为 (P + 1)/2。
表示法
| 项 | 说明 |
|---|---|
 | 极值分布的位置参数的极大似然估计 |
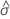 | 极值分布的尺度参数的极大似然估计 |
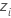 | 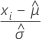 ,基于最小极值分布中位置和尺度参数的 MLE 估计值的居中观测值 ,基于最小极值分布中位置和尺度参数的 MLE 估计值的居中观测值 |
| t | 自由度为 n − 1 且非中心参数为 δP 的非中心 t 分布的第 α 个百分位数。 |
| 1 - α | 公差区间的置信水平 |
| P | 公差区间的范围(区间中的目标最小总体百分比) |
| n | 样本中的观测值个数 |
- Lawless, J. F. (1975)。Construction of tolerance bounds for the extreme-value and the Weibull distribution(极值和 Weibull 分布的公差限构造)。Technometrics(技术计量学),第 17 期,第 255 到 261 页。
Weibull 分布
- Minitab 取数据的自然对数。
- Minitab 使用最小极值分布的公差区间过程来计算已变换数据的公差区间。
- Minitab 对从上一步中获得的公差区间限值取指数,以将区间变换为原始数据的尺度。
最大极值分布
- Minitab 将数据乘以 −1。
- Minitab 使用最小极值分布的公差区间过程来计算已变换数据的公差。
- Minitab 对从上一步中获得的公差区间限值取指数,以将区间变换为原始数据的尺度。
有关适用于最小极值分布的公式,请转到最小极值分布部分。
Logistic 分布
Minitab 根据 Bain 和 Engelhardt1 计算近似 (1 − α, P) 公差区间,其中 1 − α 是置信水平, P是覆盖率(区间中 目标最小总体百分比)。下限公差系数的公式与上限公差系数的公式不同。
单侧 Logistic 公差限
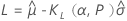

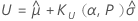

双侧 Logistic 公差区间
该分析为具有邦弗朗尼不等式2的逻辑分布生成近似的双侧公差区间。在计算单侧公差限的公式中,这种近似方法将 α 替换为 α/2,将 P 替换为 ( P + 1)/2。
表示法
| 项 | 说明 |
|---|---|
 | 较低的公差系数 |
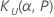 | 公差系数上限 |
| Zα | 标准正态分布的上 α 个百分位数,相当于下 1 −α 个百分位数点 |
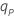 | log(p) − log(1 − p),标准逻辑分布的 p × 100 个较低的百分位数 |
| C11 | 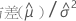 |
| C22 | 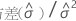 |
| C12 | 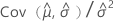 |
 | Logistic 位置参数的极大似然估计 |
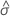 | Logistic 尺度参数的极大似然估计 |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
对数 Logistic 分布
- Minitab 取数据的自然对数。
- Minitab 使用 Logistic 分布的公差区间过程来计算已变换数据的公差区间。
- Minitab 对从上一步中获得的公差区间限值取指数,以将区间变换为原始数据的尺度。
有关适用于 Logistic 分布的公式,请转到 Logistic 分布部分。
Anderson-Darling 检验
Minitab 使用 Anderson-Darling 统计量执行拟合优度检验。
设 Z = F(X),其中 F(X) 是累积分布函数。假设样本 X1, .., Xn 给出值 Z(i) = F(Xi),i=1,.., n。按升序重新排列 Z(i),Z(1) < Z(2) <...<Z(n)。然后按如下公式计算 Anderson-Darling 统计量 (A2):
- A2 = –n - (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
将针对每个分布计算修正的 Anderson-Darling 拟合优度检验统计量。P 值基于由 D'Agostino 和 Stephens 给定的表格。1如果没有在表中找到精确的 p 值,Minitab 将根据插值法使用 p 值范围来计算 p 值。
